
Lectures part1
.pdf- 111 -
осями сечения. Таким образом, нейтральный слой при чистом изгибе проходит через линию центров тяжести поперечных сечений.
Тем же путем вычислим момент относительно оси у
M y (x)= −òz(σxdF )= −òz(− EκydF )= Eκò yzdF = EI yz κ = 0 . |
(10.27) |
||
F |
F |
F |
|
Момент M y (x) в данной задаче также равен нулю, т.к. изгиб рассматривается моментом M z (x). Знак минус в формуле приходится ставить потому, что поло- жительное напряжение σx , действующее на площадку с положительной коор-
динатой z , даёт отрицательное значение момента с точки зрения правила зна- ков эпюр внутренних силовых факторов. Из трёх сомножителей, от которых зависит M y (x), нулю может быть равен только центробежный момент I yz = 0 ,
но тогда выбранные оси, в которых ведется решение задачи изгиба, должны быть не только центральными, но и главными осями сечения.
Этот результат показывает также, что для плоского изгиба требование симметрии сечения является избыточным. Очевидно, что если нагрузка будет лежать в плоскости одной из главных центральных осей произвольного, посто- янного по длине сечения, то момент относительно этой оси окажется равным нулю, и изгиб будет происходить в той же плоскости, т.е. будет плоским.
Получим теперь выражение для момента M z (x), |
который в отличие от |
|
N(x) и M y (x) реально действовал в сечении |
|
|
i=∞ |
Mi = −ò y(σxdF ) . |
|
M z (x)= å |
(10.28) |
|
i=1 |
F |
|
Здесь снова для достижения равенства необходимо ставить знак минус. Под- ставляем в последнее соотношение выражение для нормального напряже- ния σx (10.23), используем выражение для момента инерции, а также снова учи-
тываем постоянство величин Е и κ
M z (x)= −ò y(− EκydF )= Eκò y2dF = EIzκ , |
(10.29) |
|
F |
F |
|
в результате получается уравнение изогнутой оси балки:
M z (x) = EIz κ = EIz |
d 2v0 |
(x) |
. |
(10.30) |
||
dx2 |
|
|||||
|
|
|
||||
Эту формулу называют ещё уравнением упругой линии или соотношением упру-
гости при изгибе.
Полученная формула вполне объяснима. Естественно, что в линейной за- даче изгибающий момент оказался пропорциональным кривизне оси балки. Ко-
эффициент пропорциональности EIz называется жесткостью сечения при изгибе. Формула используется, в частности, для вычисления кривизны балки по
|
|
|
|
|
|
- 112 - |
|
значениям эпюры изгибающих моментов M z (x) : |
|
||||||
κ = |
d 2v0 (x) |
= |
M z (x) |
, |
(10.31) |
||
dx2 |
|
EIz |
|
||||
поскольку Iz (осевой момент инерции) сечения может быть вычислен, а модуль
упругости материала Е должен быть известен.
Подставив выражение для кривизны в (10.31), получаем формулу для вы- числения нормальных напряжений при изгибе:
σx = − |
M z (x) |
y . |
(10.32) |
||
Iz |
|
||||
|
|
|
|||
Это соотношение позволяет находить нормальные напряжения по значениям эпюры M z (x) .
|
y |
|
|
y |
|
|
M z (x) |
z |
0 |
|
|
|
|
|
|
||
0 |
x |
|
|
|
M z (x) |
|
σx = −Eκy = − |
M z (x) |
y |
x |
|
|
|
Iz |
|
||
|
|
|
|
|
|
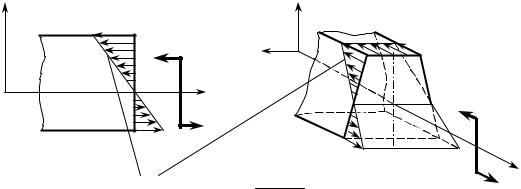
Рис. 10.11
Распределение нормальных напряжений σx по поперечному сечению, за-
данное формулами (10.23) и (10.32), представлено на рис. 10.11, где оно показано как на виде сбоку со стороны оси z, так и на пространственном изображении сече- ния. Отметим, что при положительном моменте M z (x) и положительной коорди- нате y напряжение σx отрицательно, т.е. вызывает сжатие верхних (расположен-
ных в положительной полуплоскости оси у) продольных «волокон» балки. Ось z отделяет зону сжатия от зоны растяжения, поэтому является нейтральной линией.
Линия пересечения нейтрального слоя с плоскостью сечения называется ней- тральной линией. Нормальное напряжение на нейтральной линии равно нулю.
Из формулы (10.32) видно, что поскольку характеристики материала в неё не входят, нормальные напряжения при чистом изгибе не зависят от материала стержня. Отсюда следует, что при одинаковых моментах в одинаковых по форме балках из резины и из стали напряжения будут одинаковыми. (Следует иметь в виду, что таким свойством обладают только простые задачи, в общем случае на- пряжения в конструкциях зависят от свойств их материалов.) Зависит же от свойств материала (от модуля упругости) кривизна оси изогнутого стерж-
- 113 -
ня (10.31).
Единственные напряжения на площадках, связанных с поперечными се- чениями, σx нами найдены. Деформации εx легко найти с помощью закона Гу-
ка для растяжения-сжатия по нормальным напряжениям, по ним с помощью коэффициента Пуассона по формулам определяются εy и εz .
Прогибы балки при чистом изгибе. Гипотеза недеформируемости сечения в своей плоскости.
Дважды проинтегрировав уравнение изогнутой оси балки (10.31) в преде- лах от 0 до x, найдём сначала углы поворота поперечных сечений θ(x) , а затем
прогибы v(x)
x d 2v (x) |
|
= |
x |
M |
z |
(x) |
|
|
|||||||
ò |
|
0 |
|
|
dx |
ò |
|
|
|
dx , |
(10.33) |
||||
|
dx2 |
|
|
|
|
||||||||||
xн |
|
|
|
|
xн |
EIz |
|
|
|
||||||
откуда, учитывая, что в данной задаче M z (x) = const , EIz = const : |
|||||||||||||||
dv0 (x) − dv0 (x) |
|
|
|
= |
M z (x) (x − x ) , |
|
|||||||||
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
н |
|
dx |
|
|
|
dx |
|
|
|
x=xн |
|
|
EIz |
|
|||
|
|
|
|
|
|
|
|
|
|||||||
но dv0 dx = θ(x) , поэтому |
|
|
|
|
|||||||||||
θ(x) − θ(xн ) = |
M z (x) |
(x − xн ) . |
(10.34) |
||||||||||||
|
EIz |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Предполагая, что балка закреплена на левом торце, как показано на |
|||||||||||||||
рис. 10.2, |
следует |
|
снова |
|
считать, что если |
x = xн = 0, то θ(x = 0) = 0 и |
|||||||||
v(x = 0) = 0 , поэтому вместо (10.34) получаем |
|
||||||||||||||
θ(x) = |
M z (x) |
|
x |
= κ x . |
|
|
(10.35) |
||||||||
|
EIz |
|
|
|
|||||||||||
Новое интегрирование в тех же пределах даёт
v0 (x) = M z (x) x2 = κ x2 . 2EIz 2
Затем, по прогибам можно определить и перемещения точек мощью формулы (10.20):
u(x, y) = − y M z (x)
EIz
где функция u от z не зависит по гипотезе плоских сечений.
(10.36) u(x, y) с по-
(10.37)
Важнейшие величины задачи чистого изгиба определены, и её можно в
основном |
считать решённой. Не найдены только |
угловые деформации |
γ yz (x, y, z) |
и перемещения в плоскости сечения v(x, y, z) |
и w(x, y, z). Известны |

- 114 -
лишь перемещения в направлении y оси балки v0 (x) (прогибы). Во многих за- дачах, но не всегда, величины γ yz (x, y, z) , v(x, y, z) и w(x, y, z) можно не опре- делять точно, считая, например, что сечение не деформируется в своей плоско-
сти. Это допущение называют гипотезой недеформируемости сечения в своей плоскости (вторая кинематическая гипотеза при чистом изгибе). Тогда полага- ют:
γ yz (x, y, z) ≡ 0, w(x, y, z) ≡ 0 , v(x, y, z) = v0 (x) . |
(10.38) |
Последнее равенство означает, что не делается различий между прогибом v0 (x)
(перемещением оси балки) и перемещениями других точек того же сечения в направлении оси y. Допущение оправдано при малых размерах поперечного се- чения.
Однако можно и точно отыскать эти функции в данной задаче. Проще
всего найти угловые деформации |
γ yz . Они определяются законом Гука для |
сдвига по касательным напряжениям τ yz = 0 : |
|
γ yz = τ yz G = 0 . |
(10.39) |
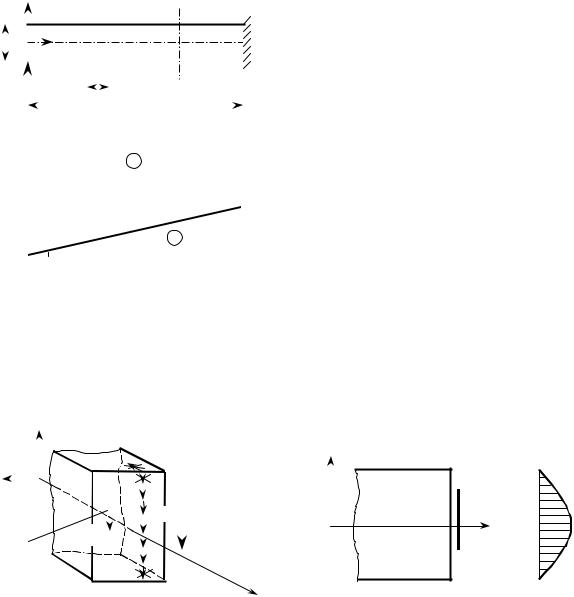
Это означает, что углы между координатными направлениями в сечении оста- ются прямыми в результате деформации. С учётом деформации в поперечных
направлениях с коэффициентом Пуассона форма поперечного сечения окажется такой, как показана на рис. 10.5. Отыскивая остальные перемещения, придём к
полному решению задачи чистого изгиба балки из системы уравнений теории упругости.
Перемещения в поперечном направлении естественно определять, интегрируя соот-
ношения Коши с учетом (10.21), например: |
|
||
∂v(x, y, z) = ε y |
= μκy ,. |
(10.40) |
|
|
∂y |
|
|
Принтегрируем по y: |
|
|
|
y |
|
y |
|
ò |
∂v(x, y, z) dy = òμκydy . |
(10.41) |
|
0 |
∂y |
0 |
|
|
|
||
Учтем постоянство множителя μκ , запишем интеграл от производной как разность значений
в точках верхнего и нижнего пределов и найдём
v(x, y, z) = v(x,0, z) + μκ |
y2 |
. |
|
(10.42) |
|
|
|
||||
|
2 |
|
|
|
|
Функция v(x,0, z) пока неизвестна. |
|
|
|||
Воспользуемся соотношением Коши для угловых деформаций |
|
||||
γxy = 0 = ∂v(x, y, z) |
+ ∂u(x, y) |
, |
(10.43), |
||
∂x |
|
∂y |
|
|
|
|
|
- 115 - |
|
откуда следует |
|
|
|
∂v(x, y, z) |
= − ∂u(x, y) . |
(10.44) |
|
∂x |
∂y |
|
|
Запишем производную в левой части равенства, подставив соотношение (10.42): |
|
||
∂v(x, y, z) |
= ∂v(x,0, z) |
+ 0 . |
(10.45) |
∂x |
∂x |
|
|
Производная же в правой части на основании формулы (10.37) даёт
∂u(x, y) = −κx . (10.46)
∂y
В результате из (10.44) получаем
∂v(x,0, z) = κ
∂x
x . (10.47)
Проинтегрировав последнее соотношение по x в пределах от 0 до x, найдём
v(x,0, z) = v(0,0, z) + κ |
x2 |
. |
|
|
|
(10.48) |
||
|
|
|
|
|
||||
2 |
|
|
|
|
|
|
||
Подставив в (10.42), получим следующее выражение для функции v(x, y, z) : |
||||||||
v(x, y, z) = v(0,0, z) + κ |
x2 |
|
+ μκ |
y2 |
. |
(10.49) |
||
|
|
|||||||
2 |
|
|
2 |
|
w(x, y, z). Используем соотношение Коши с |
|||
Аналогично поступаем для функции |
||||||||
учётом (10.21): |
|
|
|
|
||||
∂w(x, y, z) = εz = μκy . |
|
|
|
(10.50) |
||||
∂z |
|
|
|
|
||||
Интегрируем его по z в пределах от 0 до z
w(x, y, z) = w(x, y,0) + μκyz .
Применяем соотношение Коши для угловых деформаций:
γxz = 0 = |
∂w(x, y, z) |
+ |
∂u(x, y) |
|
∂x |
|
∂z |
Но u(x, y) от z не зависит, производная по z равна нулю, отсюда найдём
∂w(x, y, z) = 0 . ∂x
(10.51)
(10.52)
(10.53)
Подставим сюда (10.51) и обнаружим, что |
|
∂w(x, y,0) = 0 , |
(10.54) |
∂x |
|
следовательно, функция w(x, y,0) от x не зависит. Поэтому |
|
w(x, y,0) = w(0, y,0) . |
(10.55) |
Подставив последнее соотношение в (10.51) , получим выражение для функции w(x, y, z)
w(x, y, z) = w(0, y,0) + μκyz , |
(10.56) |
- 116 -
Теперь воспользуемся последним из соотношений Коши для угловой деформации
γ yz = 0 = |
∂w(x, y, z) |
+ |
∂v(x, y, z) . |
(10.57) |
|
∂y |
|
∂z |
|
Записав производные для функций w(x, y, z) и v(x, y, z) с помощью (10.49) и (10.56), най-
дём
∂w(0, y,0) + μκz + ∂v(0,0, z) = 0 . |
(10.58) |
|
∂y |
∂z |
|
Частные производные |
следует заменить на обыкновенные, так как каждая из |
функций |
v(0,0, z) и w(0, y,0) есть функция только одной переменной: |
|
|
μκz + dv(0,0, z) |
= − dw(0, y,0) . |
(10.59) |
dz |
dy |
|
Здесь левая часть есть функция только переменной z , правая – только y. Равенство возможно только если обе части равенства равны некоторой константе, которую обозначим α:
− dw(0, y,0) = α , |
μκz + |
dv(0,0, z) |
= α . |
(10.60) |
||
|
||||||
dy |
|
dz |
|
|||
Интегрируем первое равенство по y в пределах от 0 до y, второе – по z в пределах от 0 |
||||||
до z: |
|
|
|
|
||
w(0, y,0) = -ay + w(0,0,0) , |
(10.61) |
|||||
v(0,0, z) = −μκ |
z2 |
|
+ αz + v(0,0,0) . |
(10.62) |
||
|
||||||
2 |
|
|
|
|
|
|
Точку балки в начале координат считаем закреплённой неподвижно: |
|
|||||
v(0,0,0) = v0 (x = 0) = 0, w(0,0,0) = 0 . |
(10.63) |
|||||
Получающееся из (10.61) соотношение |
|
|||||
w(0, y,0) = -ay |
|
|
|
(10.64) |
||
означает, что происходит поворот элемента до деформации совпадавшего с осью y в плоско- сти y0z . Будем считать в качестве краевого условия, что опора препятствует такому повороту се-
чения, тогда a = 0 и w(0, y,0) = 0, а из (10.62) найдём |
|
||
v(0,0, z) = −μκ |
z2 |
. |
(10.65) |
|
|||
2 |
|
|
|
Из этого соотношения следует, что в закреплённом торцевом сечении ( x = 0) на нейтраль- ной оси ( y = 0) при z ¹ 0 происходят перемещения в направлении, противоположном вер-
тикальной оси y, и нейтральная ось искривляется выпуклостью вверх, что соответствует рис. 10.5.
Общие соотношения для функций перемещений, с учётом найденных значений констант
для принятых условий закрепления, получились по формулам (10.37), (10.49) и (10.56): |
|
u (x, y, z) = u (x, y) = -kxy , |
(10.66) |
|
κ (x2 |
+ μy2 − μz2 ) , |
- 117 - |
v(x, y, z) = |
(10.67) |
||
|
2 |
|
|
w(x, y, z) = w(y, z) = μκyz . |
(10.68) |
||
При получении этих формул мы выполнили все соотношения теории упругости, а также гра- ничные условия. Подстановкой этих формул в соотношения Коши, можно убедиться, что они дают деформации, которые по обобщённому закону Гука вызывают напряжения, удов- летворяющие уравнения равновесия. Таким образом, получено решение задачи чистого из- гиба стержня на основе соотношений теории упругости, найдены все основные величины.
Можно заметить, что принятые граничные условия не вполне соответствуют пред- ставлению о защемлении, которое используется в сопротивлении материалов. Блокированы перемещения по осям только одной точки в начале координат на левом торце балки. Кроме того, блокированы повороты элементов, совпадающих с координатными направлениями около начала координат. При таком закреплении неподвижность балки как твёрдого тела обеспечивается, одновременно допускаются перемещения в плоскости закреплённого сече- ния по осям y и z. Реализовать реально такое закрепление непросто. Чтобы полученное ре- шение было справедливо, приходится также допускать, что приложенные изгибающие мо- менты получаются в результате давлений по торцевым поверхностям балки, которые распре- делены так же, как нормальные напряжения в поперечных сечениях.
- 118 -
Тема №11. Поперечный изгиб стержней
Понятие плоского поперечного изгиба. Основные гипотезы, прини-
маемые при поперечном изгибе
Плоский изгиб, как уже было отмечено, возникает, когда нагрузка на
стержень с постоянным поперечным сечением лежит в плоскости одной из
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
главных центральных осей. |
В общем |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
X |
+ |
|
|
|
C A |
|
|
C |
+ |
|
случае момент оказывается переменным, |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а тогда, как следует из уравнения равно- |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
P |
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
весия, в сечениях действует перерезы- |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вающая сила: |
|
|
||||||
Эпюра Qy (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dM z (x) |
= Qy (x) . |
(11.1) |
||||||||||||||||||||
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Изгиб при наличии перерезывающей силы |
||||
Эпюра M z (x) |
|
|
|
|
|
|
|
|
|
M zmax |
= Pl |
|
называется поперечным. Он |
возникает, |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
например, в случае на рис. 11.1. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если на сечение в целом действует |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
перерезывающая сила, то очевидно, что |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 11.1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
она складывается из сил, приложенных в |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
каждой точке сечения в плоскости сечения (рис. 11.2). Характеризовать эти си- лы можно касательными напряжениями (давлениями в плоскости сечения):
|
|
|
|
i=∞ |
|
|
|
|
i=∞ |
|
τxy i |
|
Fi = ò |
|
τxy |
|
|
||||
|
|
Qy (x)= å |
Ti = å |
|
|
|
dF . |
||||||||||||||
|
|
|
|
i=1 |
|
|
|
|
i=1 |
|
|
|
F |
|
|
|
|
||||
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
τxy |
|
|
|
Qy (x) |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
Ti |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Fi |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x
(11.2)
Эп. τxy (y)
x
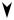 Qy (x)
Qy (x)
Рис. 11.2 |
Рис. 11.3 |
Однако касательные напряжения τxy |
не могут быть постоянными по се- |
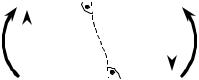
чению. Если бы они были у верхней или нижней кромки сечения, то должны были бы появиться на верхней и нижней поверхностях стержня. Но такой на- грузки на стержень в задаче нет, поэтому нет и указанных напряжений, так что
- 119 -
касательные напряжения по высоте сечения не постоянны. Они отличны от ну-
ля в середине сечения и уменьшаются до нуля при приближении к верхней и нижней его кромке. Можно предположить, что закон их распределения имеет вид, представленный на рис. 11.3. Ниже будет показано, что для прямоугольно- го сечения он действительно такой.
Qy (x) |
|
Qy (x+ ) |
Помимо |
касательных напряжений |
|||||||
|
при поперечном изгибе появляются и до- |
||||||||||
|
|||||||||||
|
|
|
|
|
|
|
|
|
полнительные |
нормальные |
напряже- |
|
|
|
|
|
C+ |
|
|
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
C |
A |
|
|
|
ния σy . Действительно, поперечный из- |
|||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
(x+ ) |
гиб вызывается поперечными силами. |
||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
Очевидно, в |
зоне приложения |
силы P |
|
M |
z |
(x) |
|
M |
z |
||||||
|
|||||||||||
|
(рис. 11.1) возникают контактные на- |
||||||||||
|
M z (x)¹ M z (x+ ) |
|
|||||||||
|
|
|
|
пряжения σy , они вызывают взаимное |
|||||||
|
|
|
Рис. 11.4 |
|
|
|
|
надавливание продольных «волокон» |
|||
|
|
|
|
|
|
|
|
|
балки. |
|
|
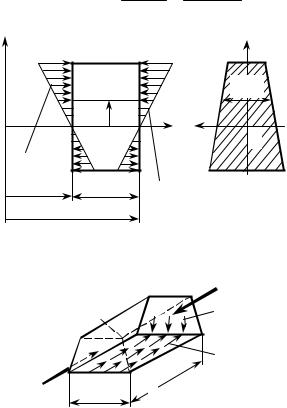
Произвольный элемент балки (рис. 11.1), мысленно выделенный из него двумя сечениями в точках C и C+ (или X и X+), оказывается нагружен несим- метрично относительно среднего поперечного сечения отрезка в точке A (рис. 11.4), поэтому он будет деформироваться несимметрично, и сечение в точке А плоским не останется. Можно предсказать и форму поперечного сече- ния после деформации. Касательные напряжения связаны законом Гука для
сдвига с угловыми деформациями
τxy = Gγ xy . |
(11.3) |
Отсюда видно, что угловые деформации распределены по высоте сечения как касательные напряжения. Но угловые деформации – это искажения прямых углов. Они будут ненулевыми в середине сечения и нулевыми у верхней и нижней его кромок. Поэтому форма сечения окажется такой, как она представ- лена на рис. 11.4 (штриховая линия).
Видим, что гипотеза плоских сечений и гипотеза ненадавливаемости про- дольных волокон нарушаются, гипотеза недеформируемости сечения в своей плоскости и при чистом изгибе была неточной. Как же вести расчет?
Методами теории упругости можно показать, что погрешности формул
чистого изгиба составляет |
|
|||
1 + |
h |
»1, |
(11.4) |
|
l |
||||
|
|
|
||
где h – высота балки, l – длина. Тогда формулами чистого изгиба можно поль- зоваться и при поперечном изгибе (10.30) и (10.32), но для длинных тонких ба- лок. С увеличением их относительной толщины погрешность будет нарастать.
- 120 -
Однако формул чистого изгиба для расчётов при поперечном изгибе не- достаточно. Касательные напряжения τxy = τ yx и нормальные напряжения на-
давливания продольных волокон σy могут вести к разрушениям и повреждени-
ям конструкций. В результате задачи при поперечном изгибе решаются при следующих гипотезах.
Считают справедливыми (приближенно) кинематические гипотезы чис- того изгиба (плоских сечений и недеформируемости сечения в своей плоско- сти). Используются (приближенно) формулы чистого изгиба для нормальных напряжений и уравнение изогнутой оси балки. Напряжения τxy = τ yx и σy учи-
тывают при поперечном изгибе по приближенным методикам, о которых ска- жем ниже, но влияниям этих величин на другие величины задачи пренебрегают.
В частности, соотношением закона Гука для сдвига (11.3) просто не пользуют- ся.
Касательные напряжения при поперечном изгибе. Формула Журавского.
Касательные напряжения при поперечном изгибе часто определяют при- ближенно, вычисляя средние касательные напряжения по сечению
|
τxy ср |
= − |
Q |
y |
(x) |
ò |
τxydF |
|
|
||
|
|
|
. |
|
|||||||
|
|
|
= F |
F |
|
|
|||||
|
|
|
|
|
F |
|
|
|
|
||
y |
C1 |
|
D1 |
|
|
D1 |
y |
|
D2 |
||
|
|
|
|
|
|||||||
|
C |
y |
|
D |
|
|
|
D b(y) |
D3 |
||
0 |
X |
X+ |
|
x |
|
z |
|
0 |
|
||
|
|
|
|
|
|
|
|
||||
σx (x, y) |
|
|
|
|
|
(x+ , y) |
|
|
|
||
|
x |
dx |
|
|
|
σx |
|
|
|
||
|
|
x+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис 11.5 |
|
|
|
|
|||
|
|
D1 |
D 2 N(x+ , y) |
C1 |
C 2 |
D |
τxy (x+ , y) |
|
D3 |
||
N(x, y) |
|
C 3 dx |
τyx (x, y) |
C |
b(y) |
|
Рис 11.6
(11.5)
Знак минус в формуле объясняется тем, что правила знаков для перерезываю-
щих сил и касательных напряжений приняты независимо. Как видно из рис. 11.2, положительные касательные напряжения дают отрицательную пере- резывающую силу. Равенство величин будет только при знаке минус в форму- ле. Из неё видно также, что среднее ка- сательное напряжение является сред- ним интегральным.
Уточненная формула для каса- тельных напряжений была найдена вид- ным русским инженером Д.И. Журав- ским в 1844 году. Для вывода этой фор- мулы рассмотрим элемент балки XX+ бесконечно малой длины при попереч- ном изгибе (рис. 11.1). Для общности
