
Lectures part1
.pdf
- 161 -
Проверка прочности и жёсткости при кручении.
Поскольку в материале круглого вала при кручении на площадках цилин- дрической системы координат действуют только касательные напряжения, то материал стержня находится в напряженном состоянии чистого сдвига. Поэто- му проверка прочности осуществляется по касательным напряжениям с помо-
щью неравенства
|
τ |
|
max ≤ [τ] . |
(14.17) |
|
|
|||
|
|
|
||
Допускаемое касательное напряжение может быть задано формулой |
||||
[τ] = τпред n , |
(14.18) |
|||
где n – коэффициент запаса, значение которого выбирается таким образом, чтобы
при максимально возможной погрешности расчета в реальной конструкции не могло быть превышено предельное значение τпред , а также, чтобы при эксплуата-
ционной нагрузке напряжения были ниже предела пропорциональности.
Допускаемые напряжения могут быть заданы и как доля допускаемых нормальных напряжений при растяжении. Значения берутся примерно такие же, как при сдвиге.
Самое большое значение касательного напряжения в стержне вычисляет- ся с помощью формулы (14.9):
|
τ |
|
|
= |
|
|
M x (x) |
|
max |
r . |
|
||||
|
|
|
|
|
|
||||||||||
|
|
|
|
||||||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
max |
|
|
|
|
I p |
|
|
|
max |
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Здесь дополнительно вводят обозначение |
|
||||||||||||||
Wp = |
I p |
, |
|
|
|
|
|
|
(14.19) |
||||||
rmax |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
где Wp называют полярным моментом сопротивления. Тогда условие |
прочно- |
||||||||||||||
сти переписывается так |
|
|
|||||||||||||
|
τ |
|
max |
= |
|
|
M x (x) |
|
|
max |
|
≤ [τ] . |
(14.20) |
||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
Wp |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
При выполнении этого условия конструкция считается прочной.
Проверка жесткости осуществляется как обычно по ограничению на ка- кой-либо параметр, характеризующий деформированное состояние, например:
|
ϕ |
|
max ≤ [ϕ] . |
(14.21) |
|
|
|||
|
|
|
||
где |
|
|||
[ϕ] = ϕпред kзап |
(14.22) |
|||
(в числителе – предельное значение угла поворота, в знаменателе коэффициент запаса, обеспечивающий при погрешностях в расчёте выполнение условия жё-
|
|
M x |
|
|
M x |
- 162 - |
||||||||||||||
|
|
|
|
|
сткости). Возможны и более сложные |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
условия жёсткости, о чём уже говорилось |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при рассмотрении вопроса в задачах рас- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тяжения-сжатия и изгиба. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
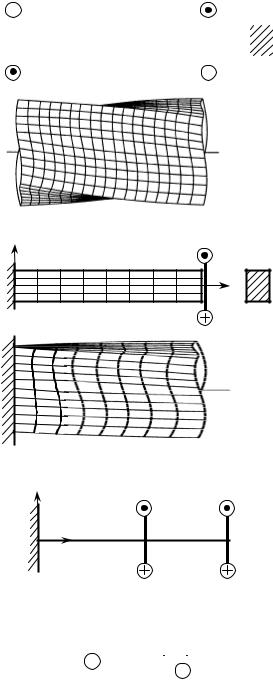
Рис. 14.12 |
y |
M x |
x |
|
Рис. 14.13 |
|
y |
M x 2 |
M x1 |
A |
C |
B |
|
x |
|
Эпюра M x (x)
|
M x1 |
+ M x 2 |
|
|
|
|
M x1 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 14.14
Кручение стержней некруглой формы
Изложенное относительно простое решение для круглого стержня, к сожале- нию, приводит к большим погрешностям
или вообще неприменимо для стержней некруглой формы. Рассмотрим экспери- мент со стержнем некруглого, например,
прямоугольного поперечного сечения (рис. 14.12, 14.13). На его поверхности до испытания наносится, как обычно, сетка взаимно перпендикулярных линий, после чего прикладывается крутящая нагрузка.
О характере деформаций можно судить по линиям сетки на поверхности и измене- нию формы самого стержня (на рисунках поперечный размер стержня после дефор- мации увеличен). В результате приходим к следующим выводам:
1.Поперечные сечения вдали от за- делки не остаются плоскими.
2.Сечение заделки остаётся плоским принудительно из-за влияния заделки, что
вызывает появление нормальных напря- жений σx вблизи сечения заделки. Они
удерживают сечения вблизи заделки от
искривления.
Выход точек из плоскости сечения называют депланацией (точнее было бы называть короблением сечений, поскольку слово «деплананировать» имело значение «разравнивать»). Блокирование депланаций и связанное с этим появление нормальных напряжений σx (которых не было при кручении
круглых стержней) называют стеснением депланаций. Кручение стержней со стеснением депланаций называют стеснённым кручением.
- 163 -
Отметим, что стеснение депланаций возникает не только вблизи заделки,
но и при быстром или скачкообразном изменении крутящего момента по длине
|
|
|
|
|
|
|
|
|
|
|
|
|
прямоугольного стержня. В случае на |
|
|
|
|
|
|
|
|
|
|
|
|
|
рис. 14.14 эпюра крутящих моментов ме- |
|
|
|
|
|
|
|
|
|
|
|
|
|
няется в точке С скачком. Это означает, |
|
|
|
|
|
|
|
|
|
|
|
|
|
что на участке AC депланации будут од- |
|
|
|
|
|
|
|
|
|
|
|
|
|
ного значения, а на участке CB большей. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Чтобы в точке С стержень остался |
|
|
|
|
|
|
|
|
|
|
|
|
|
сплошным и соседние сечения не отры- |
|
|
|
|
|
|
|
|
|
|
|
|
|
вались бы друг от друга, необходимо по- |
|
|
|
|
|
|
|
|
|
|
|
|
|
явление дополнительных нормальных |
|
|
|
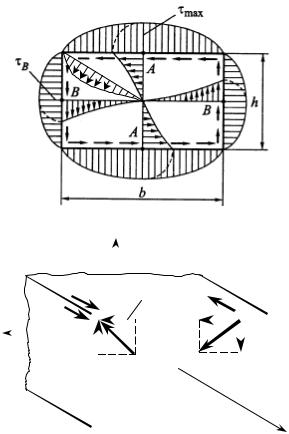
Рис. 14.15 |
|
|
|
напряжений σx , которые делают искрив- |
||||||
|
|
|
|
|
|
y |
|
|
|
|
|
лённые поперечные сечения одинаковы- |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
τxz2 |
τyx |
|
|
|
ми. Все эти явления, как показывает рас- |
|
|
τyx2 |
|
|
|
|
чёт и эксперимент, могут быть сущест- |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
венны при технической точности расчё- |
|
τzx2 |
|
|
|
|
|
|
τxz |
|
|
|
|
тов, поэтому пренебрегать ими в общем |
z |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
r |
r |
τxy |
|
||||
|
|
τxy2 |
|
|
случае нельзя. Принципиально неверной |
||||||||
|
|
|
τx2 |
τx |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
оказывается и формула для вычисления |
|
|
|
|
|
|
|
|
|
|
|
|
|
касательных напряжений круглого сече- |
|
|
|
|
|
|
|
|
|
|
|
|
x |
ния, если пытаться её использовать для |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
стержней с другой формой сечения. |
Рис. 14.16 |
Существуют аналитические реше- |
|
ния задач кручения стержней с прямоугольной и другими формами поперечно- го сечения на основе соотношений теории упругости. Однако они справедливы только для свободного (нестеснённого) кручения. Рассмотрим распределение касательных напряжений по прямоугольному поперечному сечению, получен- ное методами теории упругости (рис. 14.15). Изображены эпюры распределения касательных напряжений по различным линиям в сечении и указаны направле- ния их действия.
Часть результатов представленных на рисунке можно предсказать. Так, из условий симметрии следует, что на оси стержня нет напряжений. В углах сече- ния касательные напряжения также отсутствуют, иначе по закону парности они должны были бы появиться на наружных поверхностях стержня (рис. 14.16). Такой внешней нагрузки нет, поэтому нет и пары касательных напряжений. По тем же соображениям не может быть составляющей касательного напряжения, перпендикулярной контуру сечения, тогда касательное напряжение вблизи кон- тура сечения оказывается параллельным контуру. Таким образом, на рис. 14.16
- 164 -
из всех изображенных напряжений отлично от нуля только напряжение τxz .
Нормальных напряжений в поперечном сечении при свободном кручении нет. Наибольшим касательным напряжением могут быть его значения в точ-
ках A и B (см. рис. 14.15). На основе результатов решения задачи о кручении круглого стержня кажется, что наибольшим должно быть напряжение в более удаленной от оси стержня точке B. Однако наибольшим оказывается напряже- ние в точке A. Для его определения получается несложная формула, основанная на формуле для круглого стержня (14.20), но с поправочным коэффициентом k1 :
τmax = |
M x |
(x) |
. |
(14.23) |
|||
k1Wp |
|||||||
|
|
|
|
||||
Аналогично переписывается и формула (14.8) |
|
||||||
ξ = |
M x (x) |
. |
|
(14.24) |
|||
k2GI p |
|
|
|||||
Значения коэффициентов k1 и k2 зависят от отношения сторон прямоуголь- ника a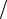 b .
b .
Подробности этого решения и решений для стержней с другими осесим- метричными формами поперечных сечений можно найти в учебной, научной и справочной литературе по механике деформируемого твёрдого тела.
Широко используются в технике тонкостенные конструкции. Их элементы в значительной части случаев можно считать тонкостенными брусьями, это напри- мер, крыло большого удлинения, фюзеляж самолета или пустотелая балка кузова автомобиля. Способы расчета таких брусьев весьма важны для практики и потому хорошо разработаны. Облегчает решение задачи свойство касательных напряже- ний разворачиваться вдоль тонкостенного контура бруса, с которым познакоми- лись при расчете двутаврового поперечного сечения. Это помогает найти точку в сечении, относительно которой происходит кручение бруса со сложной формой поперечного сечения. Указанная точка, называемая центром жёсткости (центром изгиба, центром кручения), в общем случае не совпадает с центром тяжести попе- речного сечения. В результате точно определить крутящий момент в сечении уда- ётся только после нахождения положения этого центра.
Задача кручения стержней с произвольной формой поперечного сечения решается в инженерной практике приближенно. При этом допускается погреш- ность, связанная с особенностями задачи и используемого метода решения. При необходимости технически точный результат можно получить лишь численны- ми методами на основе соотношений теории упругости.

- 165 -
Определение положения центра жёсткости для швеллера
y |
z
Py
x |
Рис. 14.17
Корытообразный профиль, представляющий собой половину двутавра, называют швеллером. Задачи растяжения-сжатия и изгиба решены нами для главных центральных осей сечения, поэтому балку с сечением в форме швеллера отнесём к та- ким осям (рис. 14.17). Ось z является единственной осью симметрии сечения, а ось y проведена через его центр тяжести. Будем считать, что внешняя по- перечная сила Py направлена вертикально вниз и
приложена таким образом, что от неё в сечении воз- никают перерезывающая сила Qy (x) и изгибающий
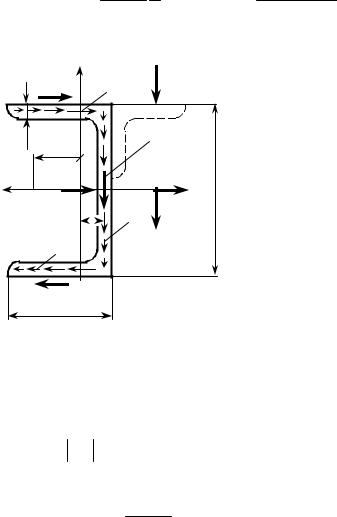
момент, но крутящий момент не возникает и балка не закручивается. На рис. 14.18 изображены фактические направления сил и касательных напряжений, действующих на площадку, из которой исходит ось x. Перерезывающая сила Qy (x) , как было по-
казано, связана с касательными напряжениями τxy и τxz , при этом
Qy (x) = Tст = òτxydF . |
|
|
|
|
|
|
|
|
|
|
(14.25) |
||||||||||
Сила Tст |
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
||||
действует, очевидно, вдоль средней линии стенки швеллера. |
|
||||||||||||||||||||
Касательные напряжения τxz дают горизонтальные силы в верхней и |
|||||||||||||||||||||
нижней полках: |
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|||||
|
B |
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Qy (x)Sz (z) |
|
|
|
|
|
|
|
|||||||||||
Tп = òτxztdz = ò− |
tdz . |
|
|
(14.26) |
|||||||||||||||||
|
|
|
|||||||||||||||||||
|
0 |
|
|
|
0 |
|
Izt |
|
|
|
|
|
|
|
|
|
ˆ |
||||
Запишем статические моменты, входящие в эту формулу для верхней |
|||||||||||||||||||||
Szв (z) и |
|||||||||||||||||||||
|
ˆ |
(z) полок: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
нижней Szн |
|
h |
|
|
|
|
|
|
|
|
|
|
|||||||||
ˆ |
|
|
|
|
|
|
|
|
ˆ |
t(B − z), |
|
|
|
||||||||
Szв (z |
= h 2) = yц.т.F = |
2 |
|
|
(14.27) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|||
ˆ |
|
= − h 2) |
|
|
|
|
ˆ |
= − |
t(B − z). |
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
Szн (z |
= yц.т.F |
2 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тогда усилия в верхней Tпв |
и нижней Tпн |
|
полках примут вид: |
|
|||||||||||||||||
T = B |
− |
Qy (x) |
|
h |
t(B − z)dz = |
Qy (x) |
|
h |
|
tB(B − z)dz = |
|
||||||||||
|
|
|
|
|
|
||||||||||||||||
пв |
ò |
|
Iz |
2 |
|
|
|
|
|
|
|
Iz 2 |
ò |
|
|||||||
|
0 |
|
|
|
|
|
|
|
|
0 |
|
||||||||||
|
= |
Qy (x)ht |
(z − B)2 |
= − |
Qy (x)htB2 |
|
; |
(14.28) |
|||||||||||||
|
|
2Iz |
|
|
|
|
2 |
|
|
|
4Iz |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
- 166 - |
|
|
|
T |
|
= B Qy (x) h t(B − z)dz = Qy (x)htB2 . |
|
(14.29) |
||||||
|
пн |
0ò |
|
Iz |
2 |
|
4Iz |
|
|
||
|
|
|
|
|
|
|
|||||
Знак минус в формуле для Tпв |
означает, что при Qy (x) > 0, сила Tпв направлена |
||||||||||
Tпв |
y |
τ |
xz |
Py |
противоположно оси z, тогда как сила Tпн на- |
||||||
|
|
|
|
|
|
|
правлена в сторону оси z. Очевидно, что силы |
||||
t |
zR |
|
|
|
|
Tст |
Tпв и Tпн образуют пару сил, так что система сил |
||||
|
|
|
|
в сечении, связанная с касательными напряже- |
|||||||
~ |
|
|
|
|
|||||||
|
Pz |
|
|
|
C |
h |
ниями, состоит из силы T |
и пары T |
, T . |
||
C |
|
|
|
|
|
ст |
пв |
пн |
|||
z |
ц.т. a |
|
|
τxy |
Rz |
Найдём линию, вдоль которой направле- |
|||||
|
|
на равнодействующая Ry |
названной системы |
||||||||
|
τxz |
|
|
|
Ry |
||||||
|
|
|
|
сил. Эта линия будет, очевидно, параллельна |
|||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
линии действия единственной не входящей в |
||
Tпн |
|
|
B |
|
|
|
|
|
пару силы Tст , а момент относительно точек |
||
|
|
|
Рис. 14.18 |
|
этой линии должен быть равен нулю, поэтому |
||||||
|
|
|
|
~ |
|
|
|||||
|
|
|
|
|
|
|
|
|
для точки C (предполагаемой точки пересече- |
||
ния линии действия силы Ry |
с осью симметрии швеллера z) должно выпол- |
||||||||||
няться условие |
|
|
|
|
|
|
|||||
|
åMC~ = 0 = −Tст (zR + a) − Tпh , |
|
(14.30) |
||||||||
где Tп = Tпв |
= Tпн |
– модуль силы в верхней и нижней полках, zR – координата z |
|||||||||
точки приложения силы Ry . Так как Tст = Qy (x) , тогда |
|
|
|||||||||
|
zR = −a − |
|
Tп |
h . |
|
|
(14.31) |
||||
|
|
|
|
|
|
Qy (x) |
|
|
|
|
|
|
Поскольку было принято, что Tп > 0 , Qy (x) > 0, h > 0, a > 0, получается |
||||||||||
отрицательное значение координаты zR , причём такое, что равнодействующая |
|||||||||||
направлена вдоль прямой, расположенной справа от оси стенки швеллера, а не |
|||||||||||
слева, как первоначально предполагалось. На рис. 14.18 точка C – действитель- |
|||||||||||
ная точка пересечения линии действия равнодействующей Ry с осью симмет- |
|||||||||||
рии – имеет координату z = zR . |
|
|
|||||||||
|
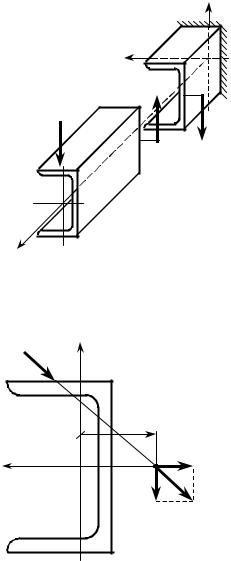
Будем теперь считать, что внешняя вертикальная сила Py направлена |
||||||||||
вниз |
и |
|
приложена, |
как это часто бывает, посередине полки |
швеллера |
||||||
(рис. 14.19). Воспользуемся методом сечений и рассмотрим равновесие отсе- |
|||||||||||
чённой части стержня без опоры. Равнодействующая R*y |
внутренних сил, вы- |
||||||||||
званных перерезывающей силой без крутящего момента, приложена к отсе- |
|||||||||||
чённой части балки в выбранном поперечном сечении и в данной задаче на- |
|||||||||||
правлена вверх. |
По закону Ньютона эта сила равна силе Ry по величине и |
||||||||||
|
|
|
|
- 167 - |
|
|
|
|
|
R*y |
противоположна ей по направлению. Из рисунка видно, что силы |
Py и |
|||||||||
образуют пару сил, которая закрутит балку. |
|
|
|
|
|
Py |
||||
|
|
|
y |
Закручивания не будет, если сила |
||||||
|
|
|
приложена в |
точке с той же координатой |
||||||
|
z |
|
|
|||||||
|
|
|
z = zR , что и сила |
R*y . Так приложить силу |
||||||
|
R* |
|
|
можно только усложнив конструкцию, доба- |
||||||
|
|
|
вив в сечении, где действует сила |
Py , пло- |
||||||
|
y |
|
|
|||||||
|
|
|
|
|||||||
|
Py |
|
Ry |
щадку, как показано на рис. 14.17. |
|
|
|
|||
|
|
|
|
При действии на балку того же сечения |
||||||
|
|
|
|
горизонтальной |
поперечной |
|
силы Pz |
|||
|
|
|
|
(рис. 14.18) закручивания не будет, если эта |
||||||
x |
|
|
|
сила действует вдоль оси симметрии швел- |
||||||
|
|
|
лера. Равнодействующая внутренних сил в |
|||||||
|
Рис. 14.19 |
|
||||||||
|
|
сечении, приложенная к рассматриваемой |
||||||||
части стержня, будет действовать навстречу вдоль той же оси симметрии. В |
||||||||||
данном случае для этой оси симметрии y = yR = 0. |
|
|
|
|
|
|||||
P |
y |
|
|
Всякая сила P, линия действия которой |
||||||
|
|
|
|
проходит через точку C с координатами yR , zR , |
||||||
|
zR |
|
|
не вызывает закручивания балки (рис. 14.20). |
||||||
|
|
|
Действительно, |
эту |
силу |
можно |
перенести |
|||
|
|
|
|
|
|
|
|
|
~ |
|
|
|
C Rz |
|
вдоль линии её действия в точку C ( P = P ), со- |
||||||
|
|
|
|
~ |
будут силы Py |
|
и Pz , |
ко- |
||
z |
|
|
|
ставляющими силы P |
|
|||||
|
~ |
|
торые, как показано выше, закручивания сече- |
|||||||
|
Ry |
|
||||||||
|
P |
|
ния не вызывают. Момент же силы P относи- |
|||||||
|
|
|
|
тельно точки C равен нулю. Эта точка и будет |
||||||
|
Рис. 14.20 |
|
|
центром жёсткости. |
|
|
|
|
|
|
|
|
|
Центром жёсткости сечения балки на- |
|||||||
|
|
|
|
|||||||
зывается такая точка в поперечном сечении, что действующая по линии, |
||||||||||
проходящей через эту точку поперечная сила, не вызывает закручивания |
||||||||||
балки. По-другому можно определить эту точку так: центром жёсткости |
||||||||||
поперечного сечения называется точка приложения равнодействующей |
||||||||||
внутренних касательных усилий, вызванных перерезывающими силами, |
||||||||||
которые не закручивают балку в данном сечении. Первое определение |
||||||||||
удобно использовать только для балки постоянного поперечного сечения. |
||||||||||
Второе можно использовать и для переменного по длине балки сечения. |
||||||||||
Центры жёсткости балки постоянного поперечного сечения образуют ось |
||||||||||
жёсткости. |
|
|
|
|
|
|
|
|
|
|
- 168 -
Видно, что центр тяжести сечения и центр жёсткости представляют собой в общем случае разные точки. Чтобы найти положение центра жёсткости, надо знать закон распределения касательных напряжений от сдвига по сечению, а эта задача не решается для сечений общего вида в рамках сопротивления мате- риалов. Внешняя нагрузка создаёт крутящий момент именно относительно цен- тра жёсткости, и если его положение неизвестно, то невозможно и точно ука- зать значение крутящего момента. Ещё больше усложняется задача, если балка имеет непостоянное по длине поперечное сечение, и центры жёсткости сечений образуют кривую или разрывную линию. Всё это указывает на особую слож- ность задач, содержащих проблему кручения стержня произвольного попереч- ного сечения.

- 169 -
Тема №15. СПОСОБЫ СНИЖЕНИЯ ВЕСА СТЕРЖНЕВЫХ
КОНСТРУКЦИЙ
Равнопрочный стержень при растяжении-сжатии.
|
|
|
|
|
|
y |
|
|
Ясно, что инженер должен создавать конструкцию не толь- |
||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
ко прочную и жёсткую, но и по возможности лёгкую. Последнее |
||||||
|
|
x |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
требование особенно важно в авиации, но его приходится учиты- |
|||||
|
|
|
|
|
|
|
|
|
вать и во всех других областях техники. |
|
|||
|
|
|
|
|
|
|
|
|
|
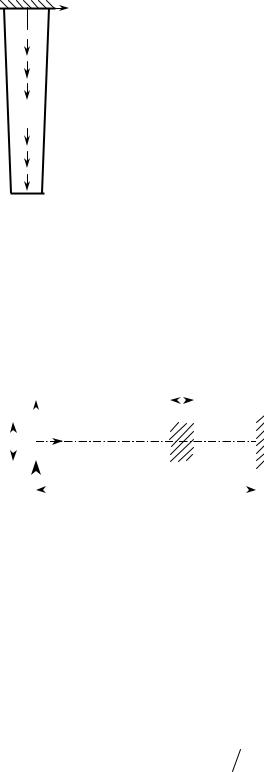
Если консольный стержень подвержен действию осевой |
|||
|
|
|
|
|
|
|
|
|
растягивающей нагрузки на конце (рис. 15.1), то во всех точках |
||||
|
|
|
|
|
|
|
|
|
всех его поперечных сечений возникают только одинаковые |
||||
|
|
|
|
|
|
|
|
|
нормальные напряжения: |
|
|||
|
|
|
|
P |
|
|
|||||||
|
|
|
|
|
|
σ = |
P |
|
|||||
|
|
|
|
|
|
|
|||||||
|
Рис. 15.1 |
|
|
|
. |
(15.1) |
|||||||
F |
|||||||||||||
Воспользовавшись условием прочности по нормальным напряжениям |
|
||||||||||||
|
|
|
|
σx = |
P |
≤ [σ]раст , |
(15.2) |
||||||
|
|||||||||||||
|
|
|
|
|
|
|
|
F |
|
||||
выберем площадь поперечного сечения стержня равной |
|
||||||||||||
|
|
|
|
F = |
|
P |
|
||||||
|
|
|
|
|
. |
(15.3) |
|||||||
[σ]раст |
|||||||||||||
Подстановка такого значения площади в (15.1) приводит к равенству |
|
||||||
σx = [σ]раст , |
|
|
|
|
(15.4) |
||
|
которое выполняется для всех точек всех поперечных сечений. |
||||||
y |
Конструкции, напряжения в которых во всех точках равны до- |
||||||
x |
пускаемым, называются равнопрочными. В этом случае в стерж- |
||||||
|
|||||||
|
не не будет лишнего материала, который можно было бы убрать, |
||||||
qx |
не перегрузив его при этом. Очевидно, что стержень оказывается |
||||||
оптимальным по весу, как и всякая равнопрочная конструкция. |
|
||||||
|
|
Если вдоль оси стержня действует ещё и растягивающая |
|||||
|
распределённая |
нагрузка |
постоянной |
интенсивности |
qx |
||
|
(рис. 15.2), то осевая сила в произвольном сечении рассчитыва- |
||||||
P |
ется так: |
|
|
|
|
|
|
Рис. 15.2 |
|
N(x)= P + qx (l − x) , |
|
(15.5) |
|||
нормальное напряжение в произвольном сечении: |
|
||||||
σx (x)= |
P + qx (l − x) |
. |
|
|
(15.6) |
|
|
F |
|
|
|
|
|||
|
|
|
|
|
|
|
|
Наибольшее напряжение возникает в сечении заделки: |
|
|
|||||

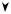
 q
q P
P