
Lectures part1
.pdf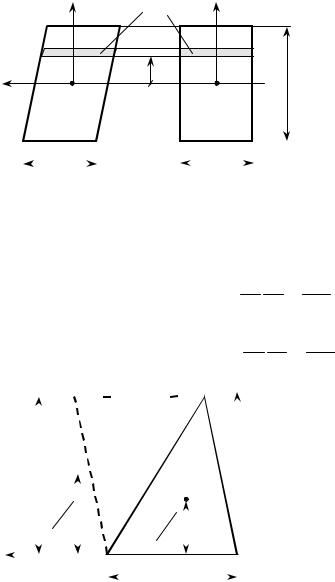
|
pD4 |
|
- 101 - |
|
Iz = |
. |
(9.27) |
||
64 |
||||
|
|
|
В силу симметрии центробежный момент снова нулевой: I yz = 0 .
Рассмотрим параллелограмм (рис. 9.10). Осевой момент параллелограмма относительно центральной оси zc , параллельной основанию, равен осевому
моменту инерции прямоугольника с теми же основанием и высотой, поскольку площади этих фигур F, их элементы dF и координаты y равны
Izc = |
bh3 |
. |
(9.28) |
|
12 |
||||
|
|
|
|
|
|
Момент |
инерции |
треугольника |
|
yc |
dF |
yc |
относительно |
оси z1 , проходящей по |
||
|
|
|
его средней линии, равен, как видно из |
|||
zc |
y |
|
рис. 9.11, половине момента инерции |
|||
h |
параллелограмма с тем же основанием |
|||||
|
|
|||||
и высотой
|
|
|
|
|
|
|
|
|
|
|
Iz |
= |
1 bh3 |
= |
bh3 |
. |
(9.29) |
|
|
b |
|
|
|
b |
|
2 12 |
24 |
||||||||
|
|
|
|
|
1 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Перейдя по формулам (9.14) сначала к |
||||||
|
|
|
|
|
Рис. 9.10 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
моменту |
инерции относительно цен- |
||||||||
тральной оси zc , |
|
|
|
|
|
||||||||||||
а затем к моменту инерции относительно оси, |
проходящей |
||||||||||||||||
через основание треугольника получим ещё две полезные формулы
Izc = Iz1
Iz = Izc
æ h |
ö2 |
F = |
bh3 |
|
||
- ç |
|
|
÷ |
|
|
|
|
24 |
|
||||
è 6 |
ø |
|
|
|||
æ h |
ö2 |
F = |
bh3 |
|
||
+ ç |
|
|
÷ |
|
|
|
|
|
36 |
|
|||
è 3 |
ø |
|
|
|||
- h2 bh = bh3 , 36 2 36
+h2 bh = bh3 . 9 2 12
(9.30)
(9.31)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
h 2 |
|
|
|
|
|
|
|
|
|
|
|
h |
ц.т. |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
b |
|
0 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 9.11
Формула (9.31) для треугольника легче все- го запоминается, другие же всегда можно получить, если помнить её.
Центробежные моменты для тре- угольника отличны от нуля для рассмот- ренных центральных осей, но останавли- ваться на получении формул для них не бу- дем. Их и формулы для других сечений можно найти в справочниках или учебни- ках по сопротивлению материалов.
|
|
|
|
|
|
|
|
|
|
- 102 - |
Вычисление моментов инерции сложных составных сечений |
||||||||||
Как уже было сказано, в теории расчета стержней используются главные |
||||||||||
центральные оси сечений и значения главных моментов инерции, поэтому для по- |
||||||||||
лучения результата нужно уметь находить положение этих осей и значения мо- |
||||||||||
ментов инерции для них. |
|
|
|
|
|
|
|
|
||
В простых случаях формулы могут быть получены аналитически, после чего |
||||||||||
по ним можно вычислить необходимые величины. В более сложных случаях при |
||||||||||
наличии компьютера и соответствующих пакетов программ можно воспользо- |
||||||||||
ваться численными методами, приближенно заменив бесконечные интегральные |
||||||||||
суммы конечными с большим числом слагаемых. Так можно найти положение |
||||||||||
центра тяжести, вычислить моменты инерции для произвольно выбранных цен- |
||||||||||
тральных осей, после чего по формулам (9.18) и (9.19) можно найти направления |
||||||||||
главных осей и значения главных моментов инерции. |
||||||||||
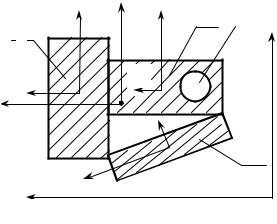
Если же вычисления проводят вручную, то экономичнее разбить сечение |
||||||||||
на ряд простых элементов (рис. 9.12), для которых положение центров тяжести |
||||||||||
y1 |
yc |
y 2 II |
III |
|
|
|
и значения моментов инерции для не- |
|||
I |
|
|
|
|
|
|
|
|
y |
которых собственных осей известно |
|
|
|
|
|
|
|
|
|
или может быть найдено в справочни- |
|
z1 |
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ках. Тогда по формулам (9.4) можно |
||
zc |
|
|
|
|
|
|
|
|
|
найти положение центра тяжести всего |
|
ц.т. y4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сечения. Далее выбрать некоторые |
|
z4 |
|
|
|
|
|
IV |
|
|
|
произвольные центральные оси yc , zc |
|
|
|
|
|
|
|
|
|
всего сечения. Их удобнее брать па- |
|
z |
|
|
|
|
|
|
|
0 |
раллельно осям большинства элемен- |
|
|
|
|
|
|
|
|
тов, образующих сечение. Для осталь- |
|||
|
Рис. 9.12 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
ных элементов (на рисунке элемент IV) |
||
следует, используя формулы поворота осей (9.16), (9.17), вычислить моменты |
||||||||||
для осей, параллельных осям yc , zc . Затем, по формулам (9.13), (9.14) для каж- |
||||||||||
дого элемента следует вычислить моменты инерции относительно осей yc , zc . |
||||||||||
После чего можно сложить одноименные моменты инерции различных элемен- |
||||||||||
тов и найти моменты инерции всего сечения I yc , Izc , I yc zc относительно осей |
||||||||||
yc , zc . Направление главных осей и главные моменты инерции определяются |
||||||||||
по моментам инерции I y |
c |
, Iz |
c |
, I y |
c |
z |
c |
с помощью формул (9.18) – 9.19). |
||
|
|
|
|
|
|
|
||||
- 103 -
ИЗГИБ СТЕРЖНЕЙ
Тема №10. Чистый изгиб стержней
Понятие плоского чистого изгиба. Кинематические гипотезы,
принимаемые при чистом изгибе
После построения общих соотношений теории упругости вернёмся к реше- нию простейших задач, к рассмотрению отдельных видов деформации стержней.
Изгибом называется деформация бруса, при которой изменяется кривиз-
на его оси. Рассмотрим прямой брус, который называют стержнем. Естествен- но, начальная кривизна у него нулевая. Стержень, воспринимающий преиму- щественно изгиб, называют балкой.
|
y |
z |
Q |
|
0 |
Рис. 10.1
|
|
Начнем рассмотрение с наиболее |
|
|
простых случаев. Таким является пло- |
|
|
ский (прямой) изгиб. Плоским (пря- |
|
|
мым) называется изгиб, при котором |
P |
|
изогнутая ось бруса – плоская кривая. |
|
Такой изгиб возникает, в частности, |
|
|
|
|
|
|
когда брус имеет плоскость симметрии |
|
x |
и в ней лежит вся нагрузка (рис. 10.1). |
|
На рисунке такой плоскостью является |
|
|
|
|
|
|
плоскость x0y , поэтому изогнутая ось |
|
|
балки будет целиком лежать в этой |
плоскости.
Обычно изгиб сопровождается перерезывающими силами в сечениях,
связанными с изгибающими моментами уравнением равновесия
dM z (x) |
= Qy (x) |
(10.1) |
||
dx |
|
|||
|
|
|||
которое записано для плоскости x0y . В каждом сечении будут одновременно
действовать и перерезывающая сила, и изгибающий момент, как было при по- строении эпюр для изгиба. И только при постоянстве изгибающего момента M z (x) по длине балки производная будет равна нулю, то есть будет равна нулю перерезывающая сила Qy (x). В каждом сечении будет действовать один изги-
бающий момент, а явление изгиба будет проявляться в чистом виде. Поэтому
изгиб при отсутствии перерезывающей силы называется чистым.
Итак, начинаем рассмотрение со случая чистого плоского изгиба. Чистый изгиб возникает, например, в балках, показанных на рис. 10.2, 10.3. Если при этом
- 104 -
нагружается одна и та же балка, то все внутренние силы (в том числе и эпюра из- гибающих моментов, а также форма изогнутой оси) будут в обоих случаях одина- ковыми. Действительно, левый момент на рис. 10.3 – это опорная реакция. Однако
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
во втором случае перемещения точек |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
при деформации оказываются неопреде- |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ленными, поэтому, когда пойдет речь о |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
перемещениях, |
будем |
рассматривать |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
случай на рис. 10.2. Когда же решаем |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Эпюра M z (x) |
||||||||||||||||||||||||||||||||||||||||||||
другие вопросы, различий между этими |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
случаями не делаем, т.е. далее рассмат- |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
риваем оба. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На балку c постоянным прямо- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 10.2 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
угольным поперечным сечением, изо- |
|||||||||||||||||||||||||||||
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
браженную на рис. 10.4, нанесем равно- |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
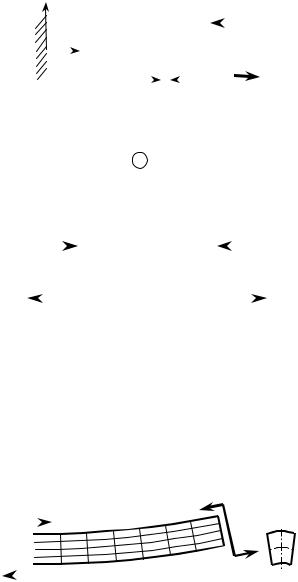
мерную сетку взаимно перпендикуляр- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ных линий, вдоль и поперек оси, а затем |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
подвергнем чистому изгибу (рис. 10.5). |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 10.3 |
По характеру |
изменений |
линий сетки |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
будем судить |
об особенностях дефор- |
||||||||||||||||||||||||||||
мирования балки. |
||||||||||||||||||||||||||||||||||||||||||||
Так, прямые углы сетки линий ос- |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
таются прямыми после деформации. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 10.4 |
Следы поперечных сечений на поверх- |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ности остаются плоскими линиями. |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
Верхние «продольные волокна» стержня |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сжимаются, нижние растягиваются. Не- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
которые искажения этой картины воз- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
можны только в зонах приложения мо- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 10.5 |
ментов. Слова «продольные волокна» |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
взяты в кавычки, поскольку в металле |
|||||||||||||||||||||||||||||
нет, конечно, никаких волокон. Характер же деформирования стержня эти слова вполне поясняют.
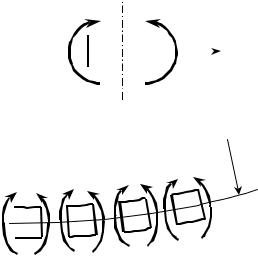
На основе этой картины деформирования формулируют следующую гипотезу.
Материальные точки бруса, до изгиба находившиеся в одной плоскости поперечного сечения, после изгиба остаются в одной плоскости, и эта плос- кость остаётся перпендикулярной продольной оси бруса, но уже изогнутой.
В формулировке гипотезы говорится о брусе, а не о балке, так как гипоте- за применяется и в более сложных случаях.
- 105 -
Гипотеза оказывается точной, что подтверждается теорией (в том числе ре- шением задачи методами теории упругости) и экспериментом. Гипотеза называет- ся гипотезой плоских сечений, или гипотезой Бернулли, по имени автора, – Я. Бернулли (1694 г.). Гипотезу называют кинематической, так как она ничего не говорит о силах, и только отражает особенности деформирования конструкций.
|
M z (x)= M |
M z (x)= M |
|
Результат эксперимента можно |
||||
|
|
|
|
|
x |
|
предсказать теоретически. Действительно, |
|
|
|
|
|
|
|
задача на рис. 10.3 имеет вертикальную |
||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
плоскость симметрии, перпендикулярную |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
плоскости чертежа, следовательно, точки |
|
|
|
Рис. 10.6 |
|
поперечного сечения на оси симметрии не |
|||
|
|
|
|
могли выйти из плоскости. Если рассмот- |
||||
|
|
|
|
|
|
|
|
|
M M M M |
M M M M |
r |
реть любую часть балки, выделенную дву- |
|||||
мя поперечными сечениями (рис. 10.6), то |
||||||||
|
|
|
|
|
|
|
|
в силу постоянства сечения и внутреннего |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
изгибающего момента M z (x) по длине эта |
|
|
|
|
|
|
|
|
|
часть снова будет симметрична, а потому должна деформироваться симметрично, и сечение на оси симметрии снова останется плоским и перпендикулярным изогну-
той оси стержня. Таким образом, гипотеза выполняется для всех сечений балки. Несложно предсказать и форму изогнутой оси балки. Если мысленно выде-
лить поперечными сечениями несколько участков балки, равных по длине (рис. 10.7), то из-за постоянства поперечного сечения и внутреннего момента по длине равные участки одинаково искривятся под действием равных моментов. Кривизна оси балки будет постоянной и отличной от нуля. Кривая с постоянной, отличной от нуля кривизной есть окружность, следовательно, изогнутая ось балки будет окружностью. Перпендикуляры к окружности (линии пересечения плоско- стей поперечных сечений с плоскостью, в которой происходит изгиб) пересекутся в центре этой окружности, поскольку это радиусы окружности.
Основные кинематические соотношения при чистом изгибе. (Тео- рия деформированного состояния при чистом изгибе.)
Общие кинематические соотношения были получены при выводе основных соотношений теории упругости. Но после введения новой кинематической гипотезы их надо дополнить. Рассмотрим балку при чистом изгибе и для определенности пе- ремещений считать её закрепленной по левому торцу (рис. 10.2).
В эксперименте установлено, что в данном случае верхние «волокна» сжимаются, а нижние растягиваются. Предполагаем, что при этом балка испы-
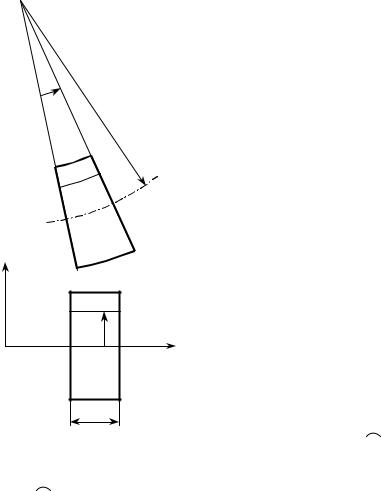
|
|
|
|
- 106 - |
|
|
|
тывает малые деформации и не разрушается. Очевидно, что тогда между зона- |
|||||||
ми растяжения и сжатия должен существовать слой, который не меняет своей |
|||||||
длины. Слой, длина которого не изменяется при изгибе, называется нейтраль- |
|||||||
ным слоем. Будем считать, что ось х проведена вдоль линии пересечения ней- |
|||||||
трального слоя с плоскостью изгиба (симметрии) балки. |
|
||||||
O* |
|
|
|
Выделим |
двумя |
поперечными |
сечениями |
|
|
|
|
элемент балки бесконечно малой длины dx = AB , |
|||
|
|
|
|
который изображен внизу на рис. 10.8 в увеличен- |
|||
|
|
|
|
ном масштабе, а в нем выделим слой CD на уров- |
|||
|
dθ |
|
|
не у. После деформации, согласно гипотезам, попе- |
|||
|
|
|
речные сечения повернутся, оставаясь перпендику- |
||||
|
|
|
|
||||
|
|
|
|
лярными изогнутой оси стержня. На рисунке поло- |
|||
|
D* |
|
r |
жения точек после деформации отмечены звёздоч- |
|||
|
C* |
B* |
|
кой. Линии поперечных сечений A*C* |
и B*D* пе- |
||
|
A* |
|
ресекутся в точке O*, |
которая будет центром ок- |
|||
|
|
|
ружности для дуги A*B* . Угол между линиями |
||||
|
|
|
|
||||
y |
|
|
|
A*C* и B*D* обозначим dθ , а радиус ок- |
|||
|
C |
D |
|
ружности r. Запишем по определению линейную |
|||
|
|
деформацию слоя CD |
|
|
|||
|
y |
|
|
εx = (dx)* − dx = |
C*D* − CD . |
|
|
0 |
A |
B |
x |
(10.2) |
|||
|
|
|
|
dx |
|
CD |
|
|
dx |
|
|
Отрезок АВ проведен по нейтральному слою, |
|||
|
|
|
поэтому |
|
|
|
|
Рис. 10.8 |
|
|
|
AB = dx = A*B* = CD = rdθ . |
(10.3) |
||||
Обозначим y* = A*C*, тогда аналогично предыдущему |
|
||||||||
C*D* = (r − y *)dθ . |
|
|
|
|
|
(10.4) |
|||
Перепишем (10.2) так: |
(r − y* )dθ − rdθ |
|
|
|
|
||||
εx = |
C*D* − CD |
= |
= − |
y* |
= −κy* , |
(10.5) |
|||
CD |
|
rdθ |
|
r |
|||||
|
|
|
|
|
|
|
|||
где радиус кривизны r заменён кривизной κ (греческая буква каппа) по форму- ле, известной из геометрии
κ = 1 . |
(10.6) |
r
Запишем среднюю деформацию отрезка AC (он не бесконечно мал) в со- ответствии с определением линейной деформации. Очевидно, что это средняя линейная деформация в направлении оси y:
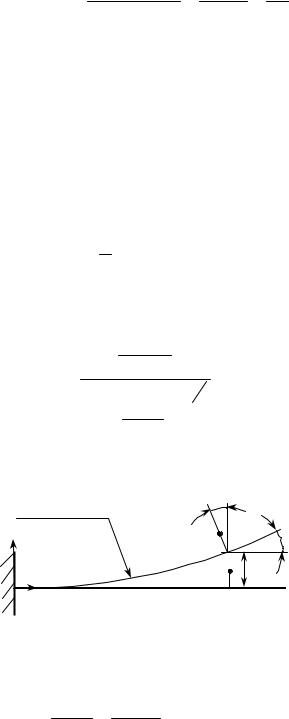
eˆ y = A*C * −AC |
= y * −y |
= y * |
- 107 - |
||||||
-1 , |
(10.7) |
||||||||
|
|
AC |
|
|
|
y |
y |
|
|
откуда |
|
|
|
|
|
|
|
|
|
y* = y + εˆ y y = y (1+ εˆ y ) . |
|
|
(10.8) |
||||||
Среднее значение деформации εˆ y |
мало, как и любое другое значение де- |
||||||||
формации, им можно пренебречь по сравнению с единицей, что приводит к |
|||||||||
следующему результату: |
|
|
|
|
|||||
y* = y . |
|
|
|
|
|
|
|
(10.9) |
|
Это означает, что можно не делать различий в размере y до и после деформа- |
|||||||||
ции, а (10.5) переписать так |
|
|
|
||||||
ex = - y |
= -ky . |
|
|
|
|
|
(10.10) |
||
|
r |
|
|
|
|
|
|
|
|
Кривизна кривой y = y(x), как известно из аналитической геометрии, оп- |
|||||||||
ределяется формулой |
|
|
|
|
|
|
|||
|
|
d 2 y(x) |
|
|
|
|
|
|
|
k = |
|
dx2 |
|
|
3 |
. |
|
|
(10.11) |
|
æ dy(x)ö2 |
|
|
|
|||||
é |
+ |
ù |
|
2 |
|
|
|
||
ê1 |
ç |
÷ |
ú |
|
|
|
|
|
|
ê |
|
è dx |
ø |
ú |
|
|
|
|
|
ë |
|
|
|
û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При малых перемещениях и дефор- |
y(x)≈ v0(x) |
|
|
|
|
q |
|
мациях уравнение изогнутой оси балки |
||
|
|
|
|
|
|
|
y(x) можно заменить функцией v0 (x), где |
||
y |
|
|
|
|
|
C* |
q1 |
v0 (x) – перемещения точек оси балки в |
|
|
|
|
|
|
|
A* |
v0 |
направлении оси y (рис. 10.9). Производ- |
|
x |
|
|
|
|
|
C |
ная функции представляет собой тан- |
||
|
|
|
|
|
A |
|
|||
|
|
|
|
|
|
генс угла наклона касательной к графи- |
|||
|
|
|
|
|
|
|
|
||
|
|
Рис. 10.9 |
|
|
|
|
ку функции в этой точке. Но при малых |
||
|
|
|
|
|
|
перемещениях и деформациях угол бу- |
|||
|
|
|
|
|
|
|
|
||
дет малой величиной, и тогда производная равна самому углу: |
|||||||||
dy(x) |
» |
dv0 (x) |
» q1 . |
|
|
(10.12) |
|||
dx |
dx |
|
|
||||||
|
|
|
|
|
|
|
|
||
Перемещения точек v0 (x) оси балки в направлении оси y называют прогибом балки. |
|||||||||
Поперечное сечение после деформации согласно гипотезе остаётся пер- |
|||||||||
пендикулярным изогнутой оси стержня. В этом случае углы q и θ1 равны: это |
|||||||||
углы с взаимно перпендикулярными сторонами. Тогда перепишем равенство |
|||||||||
(10.12): |
|
|
|
|
|
|
|
|
|
dv0 |
(x) |
|
|
- 108 - |
||
= q = q1 |
, |
(10.13) |
||||
dx |
|
|||||
|
|
|
||||
т.е. производная прогиба равна углу поворота поперечного сечения и углу на- клона касательной к изогнутой оси балки.
Знаменатель формулы (10.11) содержит квадрат малого угла, которым
при малых перемещениях и деформациях можно пренебречь по сравнению с единицей, и тогда формула кривизны кривой приобретает более простой вид:
k = d 2v0 (x) , (10.14) dx2
перепишем и (10.5) |
(x) |
|
|
|||
ex (x, y)= - |
d 2v0 |
y . |
(10.15) |
|||
dx2 |
|
|||||
|
|
|
||||
В данной формуле предполагается зависимость εx от x и y , что выполняется в об- щем случае изгиба. При чистом изгибе κ = const , поэтому и зависимости εx от x
не будет, зависимости же от z нет, поскольку принята гипотеза плоских сечений. Не будет зависимости от z и для функции осевых перемещений u = u(x, y).
Нетрудно видеть, что точки балки при изгибе получат горизонтальные перемещения u(x, y) вдоль оси х. Действительно, воспользуемся ещё одним из
соотношений Коши (8.21)
∂u(¶x, y) = ex (x, y). (10.16) x
Проинтегрируем его в пределах от начального значения xн до текущего х
u(x, y)- u(xн , y)= òx ex (x, y)dx . |
(10.17) |
xн |
|
Подставив сюда (10.15), получим
u(x, y)- u(xн , y)= -y òx d 2v02(x)dx = xн dx
édv |
0 |
(x) |
|
dv |
0 |
(x) |
|||
= -yê |
|
|
|
- |
|
|
|||
dx |
dx |
||||||||
ë |
|
||||||||
ù |
= -y[q(x)- q(xн )] |
(10.18) |
ú |
||
xн û |
|
|
Теперь учтём граничные условия задачи и определим константы интегри- рования. В закреплённом сечении (при x = xн ) отсутствуют перемещения точек
и углы поворота поперечных сечений, поэтому
u(xн , y)≡ 0, θ(xн )= 0 , |
|
(10.19) |
|||
и из (10.18) получаем |
dv0 (x) |
|
|
||
u(x, y)= -yq(x)= -y |
. |
(10.20) |
|||
dx |
|
||||
- 109 -
Из (10.20) видно, что горизонтальные перемещения точек обусловлены в данном случае поворотами поперечных сечений вследствие прогибов балки. На нейтральном слое при y = 0 они нулевые, а по высоте балки меняются по ли-
нейному закону.
С помощью коэффициента Пуассона и формулы (10.5) легко найти де- формации εy и εz :
ε y = −μεx = μκy , εz = −μεx = μκy . |
(10.21) |
По гипотезе плоских сечений |
|
γxy = γxz = 0, |
(10.22) |
так как соответствующие прямые углы при деформации не искажаются. Заметим, что деформацию εy можно считать ненулевой, поскольку ра-
венство (10.9) считается справедливым только приближённо. Но тогда переме- щения v изменяются по высоте сечения. Из-за деформаций с коэффициентом
Пуассона в поперечных к растяжению направлениях возникают переменные по координатам y и z перемещения v и w. Это приводит к изменению формы попе- речного сечения в своей плоскости в результате деформации (рис. 10.5). Опре- деление величины перемещений v и w и угловой деформации в плоскости сече- ния γ yz рассмотрим позже.
Уравнение изогнутой оси балки и формулы для нормальных напря-
жений при изгибе
Подставим известные выражения для линейных и угловых деформаций в обобщённый закон Гука во второй форме (8.40) и получим для напряжений
σx = λε* + 2Gεx = |
|
|
|
μE |
|
|
|
|
(εx + εy + εz )+ |
E |
|
|
|||||||||||||
|
|
|
|
|
|
εx |
= |
|
|||||||||||||||||
(1+ μ)(1− 2μ) |
(1+ μ) |
|
|||||||||||||||||||||||
= |
|
μE |
(ε |
|
− 2με |
|
)+ |
|
|
E |
|
ε |
|
= Eε |
|
= −Eκy , |
|
|
|||||||
(1 |
+ μ)(1− 2μ) |
x |
x |
|
(1+ μ) |
x |
x |
|
|
||||||||||||||||
|
|
μE |
|
|
|
|
|
|
|
E |
|
|
|||||||||||||
σy = λε* + 2Gεy = |
|
|
|
|
|
|
(εx − 2μεx )− |
|
|
|
|
||||||||||||||
|
|
|
|
μεx = 0 , |
(10.23) |
||||||||||||||||||||
(1+ μ)(1− 2μ) |
(1+ μ) |
||||||||||||||||||||||||
σz = λε* + 2Gεz = |
|
|
|
|
μE |
|
|
|
(εx − 2μεx )− |
|
|
|
E |
|
|
||||||||||
|
|
|
μεx = 0 , |
|
|||||||||||||||||||||
(1+ μ)(1− 2μ) |
(1+ μ) |
|
|||||||||||||||||||||||
τxy = Gγxy = 0 ,
τxz = Gγxz = 0 .
Касательным напряжение τyz определить сложнее. Используем диффе-
ренциальные уравнения равновесия теории упругости (8.40). В данной задаче объёмные силы равны нулю (ρx = ρy = ρz = 0 ), тогда, учитывая (10.23), найдём
|
∂τzy |
|
∂τyz |
- 110 - |
|
|
= 0, |
= 0 . |
(10.24) |
||
|
∂z |
∂y |
|||
|
|
|
|
||
С учётом парности касательных напряжений (τzy = τyz ) |
получаем, что каса- |
||||
тельное напряжение τyz постоянно по поперечному сечению, т.е. τyz = const .
Однако постоянное касательное напряжение должно появляться на поверхно- сти, а никакого внешнего касательного давления на поверхности по условию задачи нет. Поэтому константа и напряжение должны быть равны нулю:
τyz = 0. |
(10.25) |
Полученный результат свидетельствует о том, что напряжённое состоя-
ние в балке при чистом изгибе является одноосным (только sx ¹ 0), при этом
координатные площадки, связанные с поперечными сечениями, являются глав- ными площадками напряженного состояния.
Нулевые напряжения σ y = σz = 0 свидетельствуют о том, что при чистом из-
гибе отсутствует взаимное надавливание продольных «волокон». Этот факт часто принимают в качестве гипотезы, которую называют гипотезой ненадавливания про- дольных волокон. Как видим, в данном случае она может быть доказана.
Формула (10.23) для нормальных напряжений sx дает закон распределе-
ния этих напряжений по поперечному сечению балки, однако ею пока нельзя воспользоваться для вычислений, поскольку мы ещё не умеем вычислять кри- визну оси балки κ и неизвестно положение нейтрального слоя, от которого от- считывается координата y.
Нетрудно видеть, что нормальное напряжение в поперечном сечении спо- собно создавать осевую силу и изгибающий момент (рис. 10.10).
Запишем сначала осевую силу в сечении. Суммируя по площади попе- речного сечения силы, приложенные к элементарным площадкам dF , получим
|
|
|
i=∞ |
òσxdF = −òEκydF = −Eκò ydF = −EκSz = 0 , |
|
||||||||||
|
N(x)= å |
|
Ni (x)= |
(10.26) |
|||||||||||
|
|
|
i=1 |
|
|
|
|
|
F |
F |
F |
|
|||
|
|
y |
|
|
|
|
|
|
|
|
где использовано выражение |
для нор- |
|||
|
|
|
|
|
dF |
|
|
|
мального напряжения sx (10.23), учтено |
||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
постоянство величин Е и κ, а также оп- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
z |
|
|
|
|
|
|
|
|
|
|
|
ределение статического момента. Но в |
|||
|
|
|
σx |
|
|
|
|||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
y |
|
|
M |
|
задаче чистого изгиба осевая сила долж- |
||||||
|
|
|
|
|
|
|
|
|
|
|
на отсутствовать ( N(x)= 0). Из трех со- |
||||
|
|
|
|
|
|
z |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
множителей, от которых зависит N(x), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
нулю может быть равен только статиче- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Рис. 10.10 |
|
|
ский момент ( Sz = 0 ), но тогда выбран- |
|||||||||
|
|
|
|
|
|
ные оси должны быть центральными |
|||||||||
