
Lectures part1
.pdf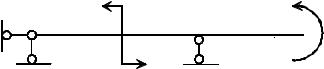
- 11 -
ваемое деформируемое тело.
Как известно, внутри твердого тела между составляющими его атомами и молекулами действуют силы взаимодействия. При приложении внешней на- грузки к твердому телу оно деформируется, изменяются расстояния между ато- мами и, следавательно, изменяются и силы межатомного взаимодействия.
Внутренними силами будем называть только дополнительно возникаю- щие от внешней нагрузки силы внутри деформируемого твердого тела (ДТТ).
Казалось бы, все просто и аналогично подходу в теоретической механике. Однако в сопротивлении материалов будут рассматриваться силы между час- тями тела, внутренние силы. Будем называть их внутренними всегда, даже то- гда, когда по отношению к рассматриваемой части деформируемого твердого тела они, с точки зрения теоретической механики, являются внешними.
Ясно, что с увеличением внешней нагрузки требуемый уровень внутрен- них сил в какой-либо части ДТТ может стать столь высоким, что окажется не-
возможным обеспечить такой уровень за счет сил сцепления частиц и начнется разрушение. Поэтому очевидно, что для решения вопроса о прочности надо сначала изучить распределение внутренних сил в ДТТ. Удобнее всего было бы сразу найти наиболее нагруженные зоны и определить в них внутренние силы, но практически сделать это обычно не удается, т.к. внутренние силы во всем теле взаимосвязаны и все внутренние силы получаются из общего решения зада- чи.
Определению внутренних сил и посвящена значительная часть механики ДТТ и сопротивления материалов.
2. Статические и динамические. Статическими будем называть силы, ди- намическими эффектами от приложения которых, т.е. ускорениями масс, мож- но пренебречь, а динамическими все прочие силы.
|
|
|
MZ1 |
M Z 2 |
3. Сосредоточенные и распре- |
|
|
|
|
|
|
|
деленные. Строго говоря, все силы, |
|
|
|
|
|
|
|
|
|
|
|
|
|
прикладываемые к деформируемому |
|
|
|
|
|
|
твёрдому телу, являются распреде- |
|
|
|
|
|
|
|
|
|
|
Рис. 1.15 |
|
ленными, но если они распределены |
|
по малой части поверхности или объёма, их можно приближенно считать со- средоточенными. Сосредоточенные силы будем изображать, как обычно, в виде вектора. Помимо сил будут рассматриваться и сосредоточенные моменты. Два способа изображения этих моментов показаны на рис. 1.15. Первый способ по- зволяет точно указать поперечное сечение балки, в котором приложен момент, второй используется в случаях, когда место приложения момента очевидно. Напомним, что момент также является векторной величиной, его изображение в
- 12 -
виде вектора в отдельных случаях также будет использоваться.
В сопротивлении материалов встречаются три вида распределённой на- грузки. Это нагрузки, распределённые по объёму, поверхности и длине. Объём-
ными называются силы, приложенные к каждой материальной точке тела.
Это силы веса, инерционные, электромагнитные. Если объемная нагрузка по- стоянна (например, удельный вес материала) то её можно найти, поделив вес тела на его объем:
ρ = VP .
Если материал имеет не постоянную по объему плотность, то удельный вес будет меняться от точки к точке. Его среднее значение вблизи произвольно выделенной точки А можно сосчитать, разделив вес P малого объема, выде- ленного вблизи данной точки, на этот объем V (рис. 1.16):
VP .
Считая, что направление силы веса может не совпадать с направлением осей выбранной для задачи системы координат, вес тела представим в виде век- тора, у которого могут быть три проекции. Соответственно три проекции будет
иметь и рассматриваемая величина
r |
|
P |
|
|
|
|
|
||||
ρсреднее |
= |
|
, {ρx , ρy , |
ρz } , |
|
||||||
V |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||
где в фигурных скобках даны компоненты вектора (проекции). |
|||||||||||
Вместо удельного веса (характеристики свойств материала) получился |
|||||||||||
|
|
|
|
|
|
|
|
|
s |
вектор объемной силы (характеристика на- |
|
|
|
|
|
|
|
|
|
|
|
гружения конструкции). Математически |
|
|
|
|
|
F |
|
|
|
B |
объемная сила в точке (в числе удельный |
||
|
|
|
|
|
|
|
вес) определяется с помощью предела. |
||||
|
|
|
|
|
|
|
|
|
S |
Объем рассматриваемого элемента надо |
|
|
|
|
|
|
|
|
|
|
устремить к нулю, стягивая его к точке в |
||
|
A |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
V |
|
|||||
|
|
|
|
|
|
|
|
|
пределах этого элемента, например точке А, |
||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
в которой надо определить объёмную силу: |
|
P |
|
|
|
|
|
|
r |
P , {ρx , ρy , ρz}. |
|||
|
|
|
|
|
|
ρ = lim |
|||||
|
|
|
|
|
|
|
|
|
|
V → 0 |
V |
Рис. 1.16 |
V → т. А |
|
Полученная векторная величина име- |
||
|
||
ет то же направление, что и вектор P , поскольку получена делением на ска- |
||
ляр. Определение любой из составляющих вектора ρ записывается с помощью такого же предела, например:

- 13 -
ρz = lim |
Pz . |
V →0 |
V |
V →т. А |
|
Числитель и знаменатель этой дроби стремятся к нулю, а предел к хоро- шо знакомой нам величине – удельному весу: т.е. весу единицы объема мате- риала вблизи заданной точки. Единицы измерения этой величины – Н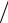 м3 (или
м3 (или
кгс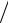 м3 ).
м3 ).
z |
|
|
|
Поверхностные силы – это, ко- |
0 |
|
r |
нечно, силы, приложенные к поверхно- |
|
x |
y |
|
st |
сти тела. Возникают они в результате |
|
||||
r |
|
r |
механического взаимодействия твердых |
|
|
sn |
r |
St |
тел, а также вследствие давления жид- |
|
r |
s |
|
|
|
Sn |
|
r |
костей или газов. Поверхностные силы |
|
|
|
||
|
|
|
S |
могут быть сосредоточенными и рас- |
|
Рис. 1.17 |
пределёнными. Рассмотрим распреде- |
||
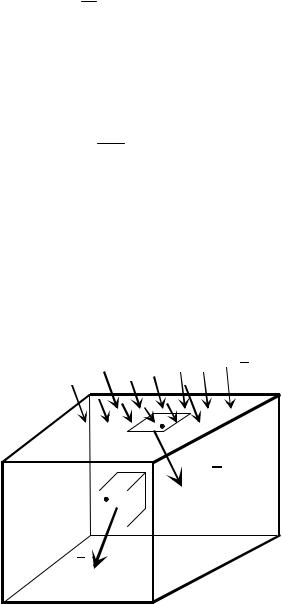
ленные поверхностные силы. Характеризуются такие силы давлением по по- верхности. В учебных курсах физики обычно изучают давление по нормали к поверхности. Однако давление может быть направлено под произвольным уг- лом к поверхности.
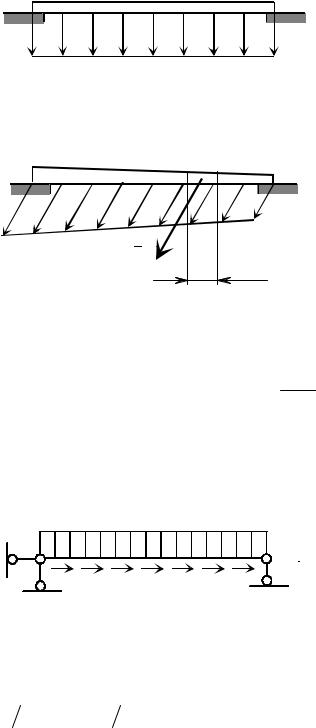
Давление же под произвольным углом к поверхности может возникать, например, при взаимодействии двух твердых тел с трением. На рис. 1.17 изо- бражен груз, лежащий неподвижно на наклонной плоскости. Сила воздействия груза на опору S может быть разложена на две составляющие: по нормали к по- верхности Sn и по касательной St . Если задана декартова система координат, в которой ось x направлена по нормали к наклонной плоскости, а две другие оси y и z параллельны наклонной плоскости (рис. 1.17, 1.18), то составляющая St может быть ещё раз разложена по направлению осей y и z: St = Sy + Sz . В итоге
|
|
|
|
|
|
сила S |
будет иметь три составляющие |
|||||||||
0 y |
|
|
r |
|
|
Sx = Sn , |
|
Sy , |
Sz , |
из которых две будут |
||||||
|
|
|
|
принадлежать наклонной плоскости. Для |
||||||||||||
r |
Sz |
|
|
|||||||||||||
z |
|
|
|
r |
каждой составляющей силы может быть |
|||||||||||
sz |
|
St |
||||||||||||||
|
|
|
|
r |
найдена |
средняя |
составляющая |
давле- |
||||||||
|
|
|
|
|
||||||||||||
|
|
|
r |
st |
|
ния. Имея в виду модули этих векторов, |
||||||||||
|
|
|
sy |
r |
|
|||||||||||
|
|
|
|
Sy |
|
запишем |
|
S y |
|
|
|
|
|
|||
|
|
|
|
|
|
sx ср = |
S |
x |
, sy ср = |
, sz ср = |
S |
z |
. |
|
||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
F |
|
|
|
|||||
|
Рис. 1.18 |
|
|
|
F |
|
|
F |
|
|||||||
|
|
|
Направления |
составляющих |
|
|
вектора |
|||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
- 14 - |
|
|
|
|
|
|
|
|
|
|
|
|
|
давления будет таким же, как у состав- |
|||||
|
|
|
|
|
|
|
ляющих вектора силы, поскольку со- |
|||||
|
|
|
|
|
|
|
ставляющие вектора давления получа- |
|||||
|
|
|
|
|
q |
|
ются |
делением |
соответствующих со- |
|||
|
|
|
|
|
|
ставляющих вектора силы на скаляр F . |
||||||
|
Рис. 1.19 |
|
|
|
||||||||
|
|
|
|
Для |
неравномерного |
давления |
||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
следует рассматривать малую площадку |
|||||
|
|
|
|
|
|
|
F на поверхности (рис. 1.16). Воздей- |
|||||
|
|
|
|
|
|
|
ствие на тело может возникать от того |
|||||
|
|
|
|
|
|
|
же груза. Можно считать, что на рис/ |
|||||
|
q |
Q |
|
|
|
|
1.16 – 1.18 изображено нагружение од- |
|||||
|
|
|
x |
|
ного и того же тела поверхностной на- |
|||||||
|
|
|
|
|
|
грузкой, которая в действительности |
||||||
|
|
|
|
|
|
|
||||||
|
Рис. 1.20 |
|
|
|
неравномерна. |
Перейдя к пределу для |
||||||
|
|
|
|
каждой составляющей по |
аналогии с |
|||||||
объёмной силой, получим |
|
|
||||||||||
|
Sy |
|
|
|
|
|
|
|||||
|
sx = lim |
S |
x , |
sy = |
lim |
, sz = |
lim |
|
S |
z . |
|
|
|
|
F |
|
|
|
|||||||
|
F →0 |
F |
|
F →0 |
|
F →0 |
|
F |
|
|||
|
F →т.В |
|
|
|
F →т.В |
|
|
F →т.В |
|
|
|
|
Это составляющие вектора давления по осям x, y, z в точке B, из которых снова |
||||||||||||
sx |
будет направлена по нормали к плоскости, а две других ( sy и sz ) лежат в |
|||||||||||
этой плоскости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогично |
записывается сам |
|
|
|
|
|
|
|
вектор давления вблизи данной точки В |
||
|
|
|
|
|
|
|||
|
|
|
q |
|
|
поверхности тела (рис. 1.16): |
||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
r |
S |
, |
|
|
|
||||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
s = lim |
F |
|
|
|
|
Рис. 1.21 |
F→0 |
|
|||
|
|
|
|
|
||||
|
|
|
|
|
|
F→т.В |
|
|
где F – площадь малого элемента вблизи данной точки, |
S – сила, прило- |
|||||||
женная к этой площади. Очевидно, |
что единицы |
измерения давления – |
||||||
Н м2 (или кгс м2 ). |
|
|
|
|||||
Забегая вперёд, скажем, что внутренние силы в твёрдом теле принято ха- рактеризовать такими же обобщенными давлениями, которые называются нор- мальными и касательными напряжениями.
В сопротивлении материалов рассматриваются объекты, два размера ко- торых значительно меньше третьего, – брусья, поэтому в сопротивлении мате- риалов рассматривается и нагрузка, распределённая по длине бруса.
Нагрузку, распределенную по длине бруса, называют ещё интенсивно-
- 15 -
стью нагрузки или погонной нагрузкой. Если стержень имеет постоянное попе-
речное сечение и нагружен собственным весом (рис. 1.19), то погонная нагруз- ка, т.е. нагрузка на единицу его длины, будет постоянной и составит
q = Q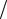 l .
l .
Если же, например, сечение бруса переменно по длине, то тогда, очевид- но, переменным окажется и q. Предположим, что направление силы веса не
|
|
|
|
совпадает с направлением осей коорди- |
|||||
|
|
|
|
нат (рис. 1.20). Взяв некоторый участок |
|||||
|
|
|
|
стержня длиной |
x и разделив его вес |
||||
|
|
|
|
Q на длину этого участка, получим |
|||||
mx |
|
|
|
среднюю |
погонную |
нагрузку |
на этот |
||
|
|
x |
участок от силы веса. Уменьшая длину |
||||||
|
|
|
|||||||
|
|
|
участка до бесконечности, придем к ма- |
||||||
|
|
Рис. 1.22 |
|||||||
|
|
тематическому |
определению |
понятия |
|||||
вектора распределенной нагрузки в данной конкретной точке оси бруса: |
|
||||||||
r |
= lim |
Q |
. |
|
|
|
|
|
|
q |
x |
|
|
|
|
|
|
||
|
x→0 |
|
Распределенная |
нагрузка |
также |
||||
|
|
|
|
||||||
|
|
|
|
может |
иметь |
три |
составляющие |
||
|
|
|
|
qx ,qy ,qz . Единицы измерения – Н/м. |
|||||
|
|
|
|
Распределенную нагрузку qy , на- |
|||||
|
|
|
|
правленную поперек оси бруса, будем изо- |
|||||
|
|
|
|
бражать так, как указано на рис. 1.19. Рас- |
|||||
mx |
|
|
M x |
пределенную нагрузку qx , |
направленную |
||||
|
|
|
вдоль оси бруса, будем изображать анало- |
||||||
|
|
|
x |
||||||
|
|
|
гично, но вместо вертикальных стрелок |
||||||
|
|
Рис. 1.23 |
будем дополнительно изображать стрелки |
||||||
h |
|
|
|
вдоль оси бруса, указывающие направле- |
|||||
|
|
|
|
ние действия нагрузки (рис. 1.21). Хотелось |
|||||
|
|
|
x |
бы подчеркнуть, |
что |
распределенная на- |
|||
|
|
|
грузка (интенсивность нагрузки) – это ве- |
||||||
|
|
|
qx |
||||||
|
|
x |
личина, отличная от просто нагрузки. Ана- |
||||||
|
|
|
|||||||
|
|
|
|
логично путь и скорость – это, по сути, |
|||||
|
|
Рис. 1.24 |
разные величины, которые не следует пу- |
||||||
|
|
|
|
тать друг с другом. |
|
|
|
||
Подобно погонной силовой нагрузке может существовать и погонная мо- ментная нагрузка. Это, например, аэродинамический крутящий момент, дейст-
- 16 -
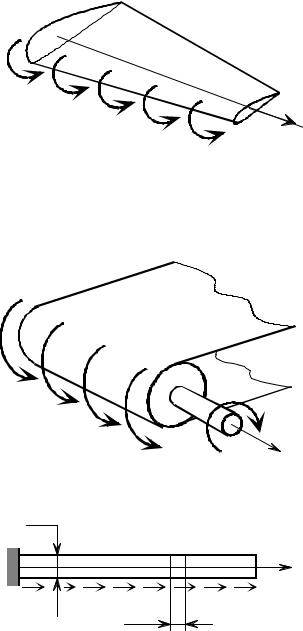
вующий на крыло (рис. 1.22), или момент сопротивления ленты транспортера, действующий на приводящий ее в движение валик (рис. 1.23).
Распределенная моментная нагрузка определяется в этом случае, как не- трудно видеть, формулой
mx = lim |
Mx . |
x→0 |
x |
Буквенный индекс в обозначениях моментов указывает на ось, относительно которой создает вращение данный погонный или обычный момент.
Переменность объемной нагрузки по высоте сечения или же распреде- ленные поверхностные силы, создающие момент относительно оси бруса, мо- гут приводить к появлению распределенных моментов mz . Например, участок бруса длиной x (рис. 1.24) будет подвержен действию момента
Mz = h2 qx x .
Распределённый момент в этом случае будет равен
mz = mz ср = |
M z |
= q x h |
, |
|
x |
||||
|
2 |
|
он не будет изменяться по длине стержня. В общем случае величина mz пере-
менна и определяется в точке формулой
mz = lim |
Mz . |
x→0 |
x |
Таким образом, очевидно, что распределенный момент тоже может быть вектором, имеющим три проекции:
m{mx ,my ,mz} .
Основные гипотезы, принимаемые в сопротивлении материалов.
Как и всякая наука, сопротивление материалов основывается на ряде ос- новополагающих гипотез, вытекающих из опыта, из практики. Рассмотрим их, не претендуя на полноту. Назовём только важные для понимания. Первые две гипотезы (или аксиомы) уже известны из курса теоретической механики.
1.Аксиома связей. Несвободное твердое тело можно рассматривать как свободное, на которое кроме заданных сил действуют реакции связей.
2.Принцип отвердевания. Предполагаем, что после того, как тело де- формировалось под действием нагрузки, равновесие тела и его частей можно рассматривать, считая тело уже абсолютно твердым. (Данная формулиров-
ка не является самой общей, она приспособлена к применению в данном курсе.)
-17 -
3.Принцип Сен-Венана. Принцип является скорее итогом решения задач механики деформируемого твердого тела (МДТТ) и сопротивления материалов,
|
чем гипотезой, закладываемой в основу |
|
q1 |
построения теории. Однако строгого |
|
|
доказательства на основе соотношений |
|
|
||
|
МДТТ он, по-видимому, пока не имеет. |
|
Q |
||
В то же время этот принцип во всех |
||
|
||
q2 |
случаях полностью подтверждается |
|
расчетом и экспериментом, имеет чет- |
||
|
||
|
кий физический смысл и очень важен |
|
|
||
Q |
для понимания характера распределе- |
|
Рис. 1.25 |
ния усилий в деформируемых твердых |
|
телах. Его формулировка вполне дос- |
||
|
тупна для восприятия и без предварительного изучения вопроса, поэтому приве- дем ее здесь. В определении использовано понятие локальной нагрузки, т.е. на- грузки, действующей по весьма малой части поверхности или объема тела.
Внутренние усилия в деформируемом твердом теле (ДТТ) вдали от точ- ки приложения локальной нагрузки не зависят от закона ее распределения, а
зависят только от ее главного вектора и главного момента. |
|
|
|||
|
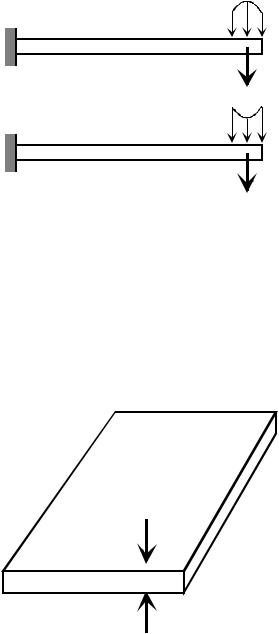
Смысл этой формулировки легко |
||||
|
пояснить на следующем примере: внут- |
||||
|
ренние усилия |
вблизи |
заделки |
на |
|
|
рис. 1.25 не будут зависеть от того, по |
||||
|
какому закону (q1 или q2 ) распределе- |
||||
Q |
ны усилия на конце консоли. Важно |
||||
|
лишь, чтобы равнодействующие этих |
||||
|
распределенных нагрузок Q в обоих |
||||
|
случаях совпадали. |
|
|
||
Q |
Принцип |
Сен-Венана имеет |
и |
||
другую формулировку, полностью эк- |
|||||
Рис. 1.26 |
|||||
вивалентную первой, но |
раскрываю- |
||||
щую другую важную особенность распределения усилий в ДТТ. Доказательст- во эквивалентности формулировок существует, но здесь не приведено.
Внутренние усилия в ДТТ быстро затухают при удалении от зоны при- ложения локальной взаимно уравновешенной нагрузки.
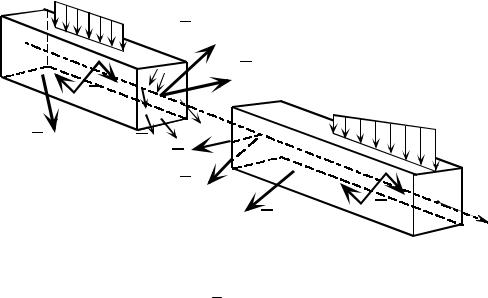
Поясним и вторую формулировку на простом примере. Если сжать плос- когубцами металлическую плиту (рис. 1.26), то внутренние усилия, возникаю- щие в ней от этой взаимно уравновешенной нагрузки, затухают на расстоянии
- 18 -
всего нескольких толщин (двух, трех или более в зависимости от требуемой точности расчета) от зоны приложения нагрузки. Весь остальной материал пли- ты практически не нагружается.
Важно отметить, что в формулировках принципа Сен-Венана речь идет о силах, а не о перемещениях точек ДТТ, последние могут быть значительными и
на бесконечно большом удалении от зоны приложения локальной взаимно уравновешенной нагрузки.
4.Принцип Д‘Аламбера. Используется при решении динамических задач. Его формулировку рассмотрим, в конце курса, когда будем изучать динамиче- ские задачи.
От названных выше гипотез отказаться невозможно. От последующих бу- дем в ряде случаев отказываться, оговаривая это всякий раз, когда нам придется так поступать. Укажем, что на отказе от этих гипотез построены многие важные разделы МДТТ, не входящие в наш курс.
5.Гипотеза сплошности. Предполагаем, что материал, из которого изго- товлены конструкции, является сплошным. Его молекулярная и кристаллическая структуры не учитываются. Эта гипотеза позволяет широко применять в сопро- тивлении материалов аппарат анализа бесконечно малых высшей математики.
6.Гипотеза однородности. Свойства материала конструкции во всех точках считаются одинаковыми.
7.Гипотеза изотропности. Свойства материала конструкции во всех на-
правлениях считаются одинаковыми. Материалы, обладающие этим свойством, называются изотропными. В первом приближении изотропными можно счи- тать металлы. Если материал имеет в разных направлениях разные свойства, то такой материал называют анизотропным. Примером явно анизотропных мате- риалов служат дерево и многие современные композиционные материалы. За- метим, что материалы могут быть анизотропными, но однородными или, на- пример, неоднородными, но изотропными.
8.Допущение о малости перемещений и деформаций (в данном курсе будут рассматриваться в основном твердые тела, которые деформируются очень мало).
Поскольку нами еще не рассмотрено математическое описание процесса де- формирования, то, видимо, нет смысла давать здесь точные количественные оценки понятия малости перемещений и деформаций. Мы будем, однако, с самого начала пользоваться этим понятием, опираясь просто на здравый смысл и жизненный опыт. Ведь очевидно, что большинство конструкций из металла, дерева деформируются под нагрузкой очень мало, практически незаметно для глаз (за исключением, напри- мер, пружин, деталей при штамповке, кузовов автомобилей при авариях). Не претен-
дуя на строгость, можно считать, что деформируются твердые тела мало, если
- 19 -
перемещения точек конструкции вследствие изменения её формы малы по сравне- нию с характерными линейными размерами конструкции.
Точные определения (новые понятия) для перемещений и деформаций, характеризующие изменение формы тела, будут введены далее. Эти величины и должны быть малыми при принятии данной гипотезы. Поэтому данное предпо- ложение назовём допущением о малости перемещений и деформаций.
Оно позволяет резко упростить построение теории и решение задач в МДТТ.
Упрощение заключается в том, что при малых перемещениях и деформациях задачу МДТТ в большинстве случаев без существенной потери точности можно линеари- зировать, т.е. упростить все уравнения, отбрасывая малые слагаемые, таким об- разом, что уравнения в результате становятся линейными. В этом заключается первое следствие допущения о малости перемещений и деформаций.
Напомним, что линейными называются уравнения, содержащие неиз- вестные или их производные (не обязательно первые) только в первой степени и не содержащие произведения неизвестных.
Из данного общего предположения о малости перемещений и деформаций следуют, по крайней мере, ещё два важнейших следствия, о которых необходимо сказать отдельно.
Во-первых, в случае малых перемещений и деформаций уравнения равновесия тела можно записывать для недеформированного состояния, т. е. для исходного состояния тела без нагрузки. Это следствие называют часто принципом начальных размеров. Использование его, по-видимому, не в меньшей степени, чем практическая потребность в результатах, продвинуло вперед построение науки и решение практи- ческих задач в 19-м веке, настолько принцип упростил задачу, существенно не сни- жая при этом в наиболее часто встречающихся случаях точности результата.
Во-вторых, линейность соотношений делает применимым принцип неза-
висимости действия сил (суперпозиции или наложения), всегда использовав-
шийся в теоретической механике для абсолютно твердых тел.
В МДТТ этот принцип теряет свою общность и оказывается справедли- вым лишь в случае малых перемещений и деформаций. Формулируется он в МДТТ так: результат воздействия на ДТТ системы сил при малых перемеще- ниях и деформациях равен сумме результатов воздействия тех же сил, при- кладываемых к телу последовательно и в любом порядке.
Таковы основные гипотезы, на которых основан данный курс сопротив- ления материалов.
- 20 -
ВНУТРЕННИЕ СИЛОВЫЕ ФАКТОРЫ В ПОПЕРЕЧНЫХ СЕЧЕНИЯХ СТЕРЖНЕЙ
Тема №2. Внутренние силовые факторы в стержне. Метод сечений
Внутренние силовые факторы в стержне
Рассмотрим стержень, находящийся в равновесии под действием внеш- ней нагрузки. Отнесем его, как уже было оговорено, к правой системе декарто- вых координат xyz, причем ось x направляем вдоль оси стержня, в качестве ко- торой выбрана линия центров тяжести поперечных сечений. (Считаем, что эта линия является неразрывной, например, как в случае постоянного по длине по- перечного сечения стержня.) Рассечем мысленно стержень произвольно вы- бранным сечением, перпендикулярным оси (поперечным сечением) на две час- ти (рис. 2.1). Ясно, что между частями тела в точках плоскости сечения дейст-
|
|
qk л |
Qл п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M j л |
|
|
|
Mл п |
|
||||
Pi л |
|
X |
л |
|
|
|
|
|
qk п |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|||||
|
Si |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||
|
Mп л |
|
X |
п |
|
|
||||
|
|
|
|
|||||||
|
|
|
|
|
||||||
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q п л |
|
|
|
|
M j п |
x |
|
|
|
|
|
|
Pi п |
|
|||
Рис. 2.1
вовали внутренние силы.
Рассмотрим, например, силы Si , действующие в каждой точке поперечного сечения с правой части на левую. Мы не знаем, как распределены эти силы по по- верхности сечения, их бесконечно много, но ясно, что данная система сил, соглас- но положениям теоретической механики, в сумме дает некоторый главный вектор Qпл и главный момент Mпл (рис. 2.1), который считаем приведенным к центру тяжести сечения, принимаемому, как было условлено, за точку оси стержня. По закону Ньютона, точно такая же система сил и такие же главный вектор и главный момент, но противоположного направления, действуют с левой части на правую:
Qлп = −Qпл , Mлп = − M пл . |
(2.1) |
Всех четыре вектора в формулах (2.1) нам неизвестны, поскольку неизвестны
