
Lectures part1
.pdf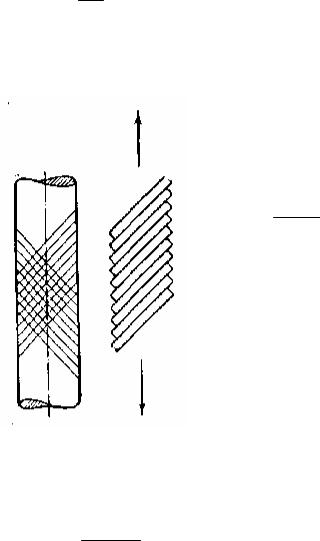
- 51 -
отсюда
m = 2EG - 1 .
Для характеристики пластических свойств материалов при растяжении определяют относительное удлинение после разрыва и относительное суже- ние площади после разрыва.
Относительное удлинение после разрыва δ –
это отношение приращения расчетной длины образца (lк − l0 ) после разрушения к начальной расчетной дли-
не l0 , выраженное в процентах, т.е.
d = lк − l0 ×100% , l0
где l0 – участок длины образца между нанесёнными
метками до испытания, на котором определяется уд- линение; lк – длина того же участка, но после разрыва
образца. Для измерения lк обе части образца по воз- можности плотно складывают, чтобы их оси образо- вывали прямую линию.
Относительное сужение площади после разрыва ψ – это отношение разности F0 и минимальной Fк
площади поперечного сечения образца после разруше- ния к начальной площади поперечного сечения образца F0 , выраженное в про-
центах:
y = F0 − Fк ×100% .
F0
Механизмы образования упругой и пластической деформации
Каков же механизм образования деформации на микроскопическом уровне? Механизм образования упругой деформации достаточно прост. Она воз- никает вследствие простого увеличения (или уменьшения при сжатии) рас- стояния между атомами и молекулами. По устранении внешних сил атомы сно-
ва занимают в кристаллической решетке свое строго определенное положение и геометрические размеры тела полностью восстанавливаются. Так объяс- няется свойство упругости.
Рассмотрим теперь процесс возникновения пластических деформаций. Опыт показывает, что образование пластических деформаций связано со сме- щениями сдвига в кристаллической решетке. Наглядное подтверждение этому
- 52 -
дает, в частности, наблюдение за поверхностью полированного образца при испытании на растяжение. В зоне общей текучести и упрочнения, т.е. при воз- никновении заметных пластических деформаций, поверхность образца покры- вается системой тонких линий (линии Людерса – Чернова) (рис. 5.7, слева). Эти линии преимущественно имеют направление, составляющее угол с осью стержня, близкий к 45°, что соответствует площадкам с наибольшим уровнем касательных напряжений. В результате соскальзывания по наклонным плоско- стям стержень удлиняется. Механизм образования этого удлинения показан в упрощенном виде на рис. 5.7 (справа).
Действительная картина более сложная, так как носит пространственный характер, и сдвиг происходит не только в одном семействе параллельных плос- костей, как это показано на рисунке, а вообще во всех семействах плоскостей, составляющих угол, близкий к 45°с осью стержня. Сдвиги происходят внутри отдельных кристаллов, и их направления в соседних кристаллах могут не сов- падать. Кроме того, смещение атомов при сдвиге происходит не по всей плос- кости одновременно, а путем последовательного перемещения начальных не- правильностей в кристаллах, которые называются дислокациями. Но в конеч- ном итоге всё же происходит сдвиг, скольжение слоёв материала друг по другу.
Поскольку пластическая деформация представляет собой последовательный процесс, а не единовременный, для её протекания требуется время. Если ско- рость деформирования увеличить, то пластические деформации не будут про- исходить в полном объёме и материал проявит более хрупкие свойства. Хруп-
костью называется свойство материалов разрушаться при малых деформа- циях.
При увеличении скорости нагружения на диаграмме исчезает площадка текучести; не образуется шейка на образце, поэтому исчезает участок падения на диаграмме; несколько повышается предел прочности; уменьшается удлине- ние при разрушении (штрихпунктирная линия на рис. 5.2). Все эти изменения соответствуют большей хрупкости материала.
При пластической деформации существует, очевидно, и упругая, связан- ная с изменением расстояний между атомами. При разгрузке искаженная фор- ма решетки восстанавливается, т.е. снимается упругая деформация. Пласти- ческая же деформация, представляющая собой проскальзывание слоев мате- риала, остается: без дополнительных сил скольжения в обратном направлении не происходит.
Весьма существенно, что процесс снятия упругой деформации происхо- дит по тем же законам, что и в начальной стадии нагружения образца. При сня- тии упругой деформации в обоих случаях сокращается расстояние между ато-
- 53 -
мами. Поэтому прямая разгрузки ZO1 (рис. 5.2) примерно параллельна прямой начального нагружения ОА.
При значительных растягивающих усилиях пластические деформации со- провождаются нарушением межкристаллических связей и связей между ато- мами, постепенно накапливаются повреждения, и образец разрушается.
Вспомним о том, что упомянутые механические характеристики и диа- грамма называются условными. Связано это с тем, что при их определении ис- пользовались данные о геометрии образца до испытания. Между тем, деформа- ции металлов перед разрушением могут достигать 20 %, 50 % и более. При этих деформациях нарушается допущение о малости перемещений и деформа- ций, и уже не безразлично, по каким размерам вычислять напряжения и дефор- мации. Истинные напряжения и деформации в материале могут значительно отличаться от условных, как и диаграмма, выражающая зависимость этих ве- личин и называемая истинной диаграммой растяжения. Получать истинную диаграмму много сложнее, и в технике пользуются именно условной диаграм- мой и соответствующими ей условными механическими характеристиками. При этом характеристики, определяемые при относительно небольших дефор- мациях (предел пропорциональности, предел текучести), незначительно отли- чаются от истинных величин. Предел же прочности (временное сопротивление) является, конечно, в полной мере условной величиной.
Заметим ещё, что свойства материалов существенно зависят от темпера- туры. Как правило, с увеличением температуры предельные напряжения пада- ют, а пластичность увеличивается, при снижении температуры наоборот. Но есть и исключения. Именно малоуглеродистая сталь при повышении темпера- туры сначала становится более хрупкой (охрупчивается) и только затем её по- ведение становится таким же, как у других материалов. Подробнее эти вопросы изучаются в курсе материаловедения.
Диаграмма растяжения дюраля и чугуна. Условный предел текучести.
Другим распространенным конструкционным материалом является дю- раль – сплав алюминия прежде всего с медью и магнием. Это уже не черный, а цветной металл.
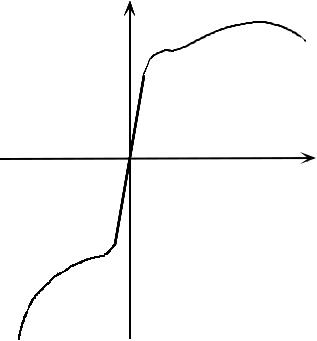
Машинная диаграмма растяжения дюраля представлена на рис. 5.8. Зна- чение предела прочности этого материала приближаются к значениям малоуг- леродистых сталей. Модуль упругости у него Е = 0,7×105 МПа, что примерно в три раза меньше, чем у сталей: Е = 2,0×105 МПа. Длина диаграммы много меньше, чем у малоуглеродистых сталей. Кроме того, диаграмма имеет и каче-

- 54 -
ственные отличия: во-первых, на диаграмме нет площадки текучести, во- вторых, нет заметного падения нагрузок перед разрушением, а значит, что на образце перед разрушением не образовывалась шейка. Всё свидетельствует о том, что это более хрупкий материал, чем малоуглеродистая сталь.
О начале процесса значительного пластическо-
го деформирования стали можно судить по площадке текучести. У дюраля ее нет, и по диаграмме не ясно, когда начинаются эти процессы. Наличие площадки текучести характерно для относительно чистых ме- таллов, её нет у легированных сталей и многих дру-
 гих сплавов, а для сплавов вообще характерна мень- l шая пластичность и отсутствие площадки текучести.
гих сплавов, а для сплавов вообще характерна мень- l шая пластичность и отсутствие площадки текучести.
Это объясняется различием в диаметрах атомов, что обычно мешает взаимному проскальзыванию слоев кристаллической решетки.
Чтобы получить представление о моменте начала значительных пласти- ческих деформаций материалов, не имеющих реальной, физической площадки текучести, вводят понятие условного предела текучести (ГОСТ 1497-84):
Предел текучести условный с допуском на величину пластической де- формации при нагружении σ0,2 – это напряжение, при котором пластическая
деформация образца достигает 0,2 % от рабочей длины образца (рабочая дли-
на образца это часть образца с постоянной площадью поперечного сечения между его головками или участками для захвата).
P |
|
|
|
Для получения условного предела текучести |
|
|
|
|
следует на оси удлинений машинной диаграммы рас- |
|
|
|
|
тяжения (рис. 5.8) отложить от начала координат с |
|
|
|
|
учётом масштаба отрезок, равный остаточному удли- |
|
|
|
|
нению образца, соответствующему допуску на вели- |
|
|
|
|
чину пластической деформации. Затем, проведя пря- |
Ο |
|
|
|
мую, параллельную прямолинейному участку закона |
|
|
|
l Гука на диаграмме, определить нагрузку, которая вы- |
|
Рис. 5.9 |
зовет такое остаточное удлинение. После чего услов- |
|||
|
|
P0,2 |
|
ный предел текучести определяется по формуле |
σ0,2 |
= |
. |
|
|
|
|
|||
|
|
F0 |
|
|
Стандарт предусматривает также другие, отличные от 0,2 % допуски на вели- чину пластической деформации. Возможны и другие методики определения условных пределов текучести (такие условные пределы текучести по-другому обозначаются).
- 55 -
Диаграмма растяжения чугуна (рис. 5.9) еще короче, чем у дюраля. Это хрупкий материал. Прямолинейный участок диаграммы чугуна, как и у боль- шинства хрупких материалов, выражен нечетко, так что закон Гука выполняет- ся весьма приближенно. Очевидно, что чугун ещё более хрупкий и менее пла- стичный материал, чем дюраль.
Диаграммы растяжения других металлов также имеют свои особенности. Материалы другой физической природы, пластмассы, композиционные мате- риалы имеют еще более яркие отличия.
Диаграммы сжатия металлов. Особенности испытаний на сжатие
Условные диаграммы сжатия металлов обычно мало отличаются от диа- грамм растяжения до предела пропорциональности, но далее различия стано- вятся существенными.
P |
Это обусловлено, во-первых, |
|
тем, что при сжатии площадь попе- |
|
речного сечения увеличивается, ус- |
|
ловные напряжения, вычисленные по |
|
первоначальной площади поперечных |
|
сечений, оказываются больше истин- |
|
ных. В результате условная диаграм- |
lма сжатия располагается выше ис- тинной диаграммы и, следовательно, выше условной диаграммы растяже- ния, если напряжения сжатия рас- сматривать по абсолютной величине.
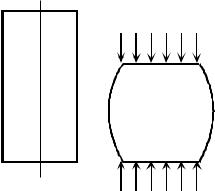
Пластичные материалы при
сжатии могут вообще не разрушаться, сплющиваясь под действием нагруз- ки; естественно, отсутствует шейка,
как правило, плохо выражена площадка текучести (рис. 5.10).
Хрупкие материалы разрушаются обычно от сдвигов под углом около 45° к оси образца. Для этих материалов характерно, что предел прочности на сжа- тие оказывается у них значительно выше предела прочности на растяжение, хотя разрушаются они также при относительно малых деформациях. Напри- мер, для чугуна предел прочности на сжатие выше, чем на растяжение, в 3 раза и более. Диаграмма же сжатия хрупких материалов по форме похожа на диа- грамму их растяжения (рис. 5.9).
- 56 -
При сжатии невозможно исключить трение по поверхностям, к которым прикладывается сжимаю- щая нагрузка. В результате в процессе нагружения
образец принимает бочкообразную форму (рис. 5.11), а напряженное состояние материала вблизи поверх- ности с нагрузкой явно перестает быть простым сжа- тием. На сжатие невозможно испытывать длинные
образцы, поскольку они теряют устойчивость при сжатии и изгибаются, тогда особенности напряжен-
ного состояния распространяются на весь образец и искажают результаты испытаний. Таким образом, для испытаний на сжатие характерна меньшая точность по сравнению с испыта-
ниями на растяжение.
Расчет на прочность по допускаемым напряжениям и расчеты на жесткость при растяжении-сжатии.
Вполне очевидно, что напряжения в конструкции не должны превышать значений, приводящих к разрушению. Однако в зависимости от обстоятельств разрушающими можно считать разные напряжения. Например, напряжения, вызывающие разрушение материала в той точке, где они действуют. Но в большинстве случаев конструкции предназначены для многократного исполь- зования. Тогда разрушающими можно считать напряжения, вызывающие большие пластические деформации. Напряжения, которые нельзя превышать, разрушающие напряжения, называют предельными (σпред ). Исходя из этого, в
качестве предельных принимают обычно предел прочности (σв ) для хрупких материалов и предел текучести (σт или σ0,2 ) для пластичных. Очевидно, что не при σв происходит разрушение, и не только при достижении σт и σ0,2 начи-
наются пластические деформации, но эти величины легко определяются из экс-
перимента и вполне могут служить и служат для оценки момента наступления опасных состояний материала.
Таким образом, ограничение по напряжениям может быть записано так:
σ < σпред , |
(5.1) |
или же |
|
σmax < σпред |
(5.2) |
Однако приближаться к ограничениям вплотную нельзя по нескольким причинам:
1) для конструкций обычно недопустимы даже малые пластические де-

- 57 -
формации, поэтому необходимо, чтобы реально действующие в конструкции напряжения были в области действия закона Гука;
2)данные о материале, о величине и характере предполагаемых нагрузок всегда имеют погрешность;
3)расчетная модель и метод расчета всегда приблизительны.
Чтобы гарантировать прочность конструкции в этих условиях, вводится коэффициент запаса прочности n, с помощью которого вычисляется допускае-
мое напряжение [σ] по формуле |
|
||
[σ]= |
σпред |
. |
(5.3) |
|
|||
|
n |
|
|
Вкачестве условия прочности при расчете по допускаемым напряжениям
взадачах растяжения принимается
σ max ≤ [σ] , |
(5.4) |
где σmax - максимальное напряжение в конструкции.
В задачах, где встречаются и растяжение, и сжатие, часто принимают, особенно для пластичных материалов, одинаковые допускаемые напряжения на растяжение и сжатие. Тогда условие прочности принимает такой вид:
≤ [σ] .
Когда допускаемые напряжения на растяжение и на сжатие разные, то соответ- ственно усложняется и условие прочности.
Если принято, что σпред = σв , то коэффициенты запаса прочности прини- маются обычно выше, чем в случае, когда σпред = σт . Причины достаточно
очевидны: за пределом прочности следует разрушение, за пределом текучести
– искажение формы конструкции, к тому же в первом случае до уровня напря- жений линейной задачи дальше, чем во втором. Поэтому различают коэффици-
ент запаса по пределу прочности (nв) и коэффициент запаса по пределу теку-
чести (nт ). Значения коэффициентов в зависимости от задачи принимают обычно в пределах nв = 2...6 , nт =1,5 ... 5 . Величина каждого из коэффициентов запаса nв и nт зависит от срока службы создаваемой конструкции, её ответст-
венности (учитываются последствия, к которым может привести ее разруше- ние), от характера нагрузок (статические или динамические), от жесткости тре- бований к весу и других параметров.
Подчеркнем, что коэффициенты запаса всегда берутся такими, чтобы на- пряжения  σ
σ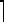 , а следовательно, и σ max конструкции, т.е. эксплуатационные на-
, а следовательно, и σ max конструкции, т.е. эксплуатационные на-
пряжения в конструкции (σэкс ), были меньше предела пропорциональности.
Это оправдывает расчет конструкций в линейной постановке и обеспечивает неизменность формы конструкции в эксплуатации.

- 58 -
Порядок расчета на прочность по допускаемым напряжениям следующий. 1. Назначают σпред для данной задачи и материала с учетом нормативных
требований или справочных данных и эксперимента.
2. Задают коэффициент запаса n с учетом особенностей задачи по отрас- левым или иным нормам или просто из опыта, после чего находят
 σ
σ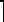 = σпредn .
= σпредn .
Примечание. В конкретных задачах, особенно для распространенных материалов, зна- чение [σ] бывает известно заранее, поскольку оно может быть определено для большого чис- ла родственных задач.
3.Рассчитывают напряженное состояние и определяют максимальные напряжения в конструкции.
4.На основании сравнения σmax с допускаемым значением (требуется, чтобы σ max ≤ [σ] ) дают заключение о прочности.
Примечание. В заключении о прочности часто указывают расчетный запас прочности конструкции по допускаемым напряжениям, который вычисляют по формуле
n[σ] = [σ] |
|
σ |
|
max . |
(5.5) |
|
|
||||
Очевидно, этот коэффициент запаса отличается от nв |
и nт . Чем он ближе к единице, тем |
||||
лучше спроектирована конструкция.
При расчёте сжатых стержней следует учитывать возможность потери стержнем устойчивости (устойчивой формы равновесия). Об этом скажем в конце курса.
Помимо расчета прочности часто приходится проверять жесткость. Ясно, что перемещения и другие параметры деформированного состояния точек кон- струкции могут быть ограничены, например для исключения возможности воз- никновения колебаний, обеспечения сборки под нагрузкой или по другим при- чинам. Здесь также можно указать некоторые предельные значения uпред , от-
носительно которых задаются новые коэффициенты запаса k, отличные от за- пасов по прочности, с помощью которых вычисляются допускаемые переме- щения [u]. Условие жесткости может иметь такой вид, например:
u max ≤ [u] = uпред .
k
Запасы по жесткости также учитывают возможные неточности в решении задачи. Задачи расчета жесткости часто встречаются на практике, (регламентации в этих вопросах обычно меньше, чем при расчете прочности). В отличие от на-
пряжений перемещения могут быть ограничены как сверху, так и снизу, а усло-
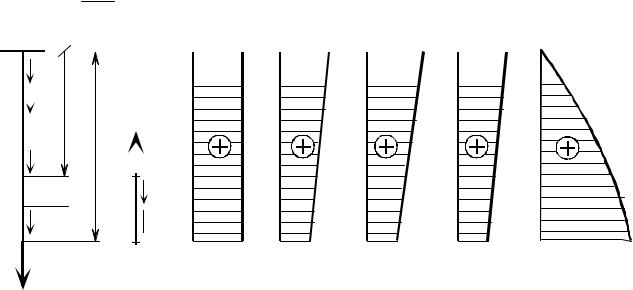
вие жесткости может иметь вид
[u]1≤ u ≤ [u]2 ,
- 59 -
что может быть необходимо, например, для обеспечения монтажа конструк- ции.
Растяжение стержня с учетом собственного веса.
Рассмотрим данный случай в качестве примера решения задачи на растя- жение. Стержень постоянного поперечного сечения нагружен силой P и собст- венным весом (рис. 5.12). Если ρ – удельный вес материала, dV – объем беско- нечно короткого участка стержня длиной dx, F – площадь поперечного сечения стержня, вес участка стержня длиной dx составляет
dQ = ρdV = ρFdx ,
то погонная осевая нагрузка запишется так qx = dQdxx = ρF = const .
|
|
|
Эпюры: |
|
qx (x) |
|
N (x) |
|
σ (x) |
|
ε (x) |
A |
u(x) |
|||
|
|
|
A |
A |
A |
A |
||||||||||
A |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||
X
B
 qx
qx
l  x
x
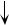 xd
xd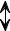
N (x)
X 
qx
B  B B B B B
B B B B B  P
P
Рис. 5.12
Применим метод сечений и найдем внутренние силы в сечениях (в дан-
ном случае это осевые силы). Из равновесия нижней части стержня BX найдем
åPxi = 0 = −N(x)+ P + qx (l − x),
тогда
N(x) = P + qx (l − x) . |
(5.6) |
По осевой силе легко найти напряжения, а затем, с помощью закона Гука, и ли- нейные деформации:
|
|
N |
|
|
P |
|
|
q |
|
|
|
|
|||||
σ = |
|
|
|
= |
|
|
|
+ |
|
|
x |
(l − x), |
|
(5.7) |
|||
|
F |
|
F |
|
|
F |
|
||||||||||
|
σ |
|
|
N |
|
|
|
|
P |
|
q |
(l − x) . |
|
||||
ε = |
|
= |
|
= |
|
|
+ |
x |
(5.8) |
||||||||
E |
|
EF |
|
EF |
EF |
||||||||||||
Перемещения определятся из общей зависимости между деформациями и пе-
ремещениями

- 60 -
u(x)= òx edx + u(xн ).
|
|
|
xн |
|
|
|
|
= 0 (рис. 5.10), а также u(xн ) = 0 |
|
|
Поскольку в данном случае xн |
(в этой точке |
|||||||||
расположена опора), то, проинтегрировав выражение для e, получим: |
||||||||||
|
) |
|
|
P |
|
qx |
æ |
x2 |
ö |
|
u x |
= |
|
|
x + |
|
çlx - |
|
÷ . |
(5.9) |
|
|
EF |
|
2 |
|||||||
( |
|
|
|
EF è |
ø |
|
||||
Все основные величины (напряжения, деформации и перемещения), ха- рактеризующие деформированный стержень, найдены. Теперь можно прове- рить прочность по допускаемым напряжениям и жёсткость. Легко видеть, что
максимальное нормальное напряжение достигается в верхнем сечении у опоры:
= FP + qFx l .
Его и следует сравнить с допускаемым напряжением.
Если задано какое-либо ограничение по жесткости, например ограниче- ния на перемещения точек оси стержня, то можно проверить и их выполнение.
Следует отметить, что формулы для каждого из полученных парамет- ров НДС (5.6) – (5.9) состоят из двух слагаемых, в каждое из которых в виде мно- жителя входит по одной из нагрузок. Это множители P и qx . Очевидно, что каж-
дое из слагаемых представляет собой часть решения от соответствующего силово- го фактора, от силы на конце стержня и от веса самого стержня, которые могут быть найдены независимо. Решение же от действия двух силовых факторов, дей- ствующих одновременно, получается сложением (суперпозицией, наложением) отдельных решений, что соответствует принципу суперпозиции линейных систем.
Система уравнений для задачи растяжения-сжатия стержня
К решению задачи можно подойти и с иной точки зрения. Имеется систе-
ма дифференциальных и недифференциальных уравнений: |
|
|||||||
ìdN |
|
= -qx , |
|
|||||
ï |
|
|
|
|||||
|
|
|||||||
ï dx |
|
|
|
|
|
|
||
ïN = sF , |
|
(5.10) |
||||||
í |
|
|
|
|
, |
|||
ïs = Ee |
|
|||||||
ï |
|
|
du |
|
|
|
||
ïe = |
|
|
|
. |
|
|||
|
dx |
|
||||||
î |
|
|
|
|
|
|||
Дифференциальные уравнения дополняются граничными условиями |
|
|||||||
u(x = x A ) = 0, |
(5.11) |
|||||||
N(x = xB ) |
= P . |
|||||||
|
||||||||
