Lectures part1

- 21 -

внутренние усилия в точках поперечного сечения. Однако векторы несложно определить, если вспомнить, что мы рассматриваем стержень, находящийся в состоянии равновесия. В этом случае, очевидно, в равновесии находится и любая часть стержня, в том числе и обе части, изображенные на рис. 2.1. Ус- ловиями равновесия левой части, согласно теоретической механике являются равенства нулю главного вектора и главного момента сил, приложенных к этой части:

записи уравнений (2.2), (2.3) заменяются равнодействующими, поэтому соот- ветствующие этим нагрузкам слагаемые из общих сумм отдельно не выделены. Символом momX ( P) обозначены моменты сил P относительно точки X.

В уравнениях (2.2), (2.3) каждое равенство содержит по одной неизвест- ной векторной величине. Каждая такая величина в этом случае может быть найдена из уравнения, в которое она входит. Таким образом, из уравнений (2.2), (2.3) следует, что искомые векторы Qпл и Mпл могут быть найдены из

равновесия левой части рассеченного стержня, а векторы Qлп и Mлп из равно- весия правой части. Последние отличаются от Qпл и Mпл только знаком. Та- ким же способом векторы Qпл , Mлп , Qпл , Mпл могут быть найдены и в любом другом сечении. Так что принципиально задача определения внутренних сил и моментов в поперечных сечениях решается просто. Заметим, что она в точно- сти также может быть решена и для трехмерного тела, однако знание сил и мо- ментов, передающихся через все сечение для трехмерного тела, практически мало полезно. Иначе обстоит дело, как увидим, в случае стержней.

Правило знаков сопротивления материалов. Метод сечений

В практических расчетах неудобно иметь дело с двумя парами векторов, отличающихся только знаком. Для того чтобы решение задачи определения внутренних усилий было однозначным, будем называть векторами внутренних интегральных силовых факторов в сечении только векторы Qпл и Mпл , т.е.

- 22 -

факторы, действующие с правой части на левую. Интегральными (т.е. суммар- ными) эти силовые факторы называем потому, что они представляют собой суммы бесконечного числа внутренних сил, действующих на каждую матери- альную точку сечения. Различают и площадки поперечного сечения. Основной (или положительной) является площадка, из которой исходит ось х, вторая площадка, в которую входит ось х, считается отрицательной.

Каждый из векторов Qпл {Qx*,Q*y ,Qz*} и Mпл {Mx*, M *y , Mz*} имеет по три

составляющих вдоль координатных осей. Название величин, совпадающих с точностью до знака с составляющими этих векторов, соответствуют той де-

Величины в левой части равенств (2.4), (2.5): Qx , Qy , Qz , M x , M y , M z , –

называются внутренними интегральными силовыми факторами в сечении. Оп-

ределение "интегральные" обычно опускают, называя их просто внутренними силовыми факторами (ВСФ), слова "силовые факторы" указывают одновре- менно на силы и моменты. Если учесть, что в каждое векторное равенство вхо- дит по три скалярных, то число уравнений в (2.2), (2.3) утроится и будет по- прежнему совпадать с числом неизвестных, что позволяет, очевидно, находить из (2.2), (2.3) ВСФ.

Замечание. Положительные направления для ВСФ на основной площадке (т.е. при от- брасывании правой части стержня), вообще говоря, могут быть выбраны произвольно, что и сделано ранее. Но, конечно, логичнее было бы принять за положительные направления со- ставляющие векторов, помеченные звездочкой.

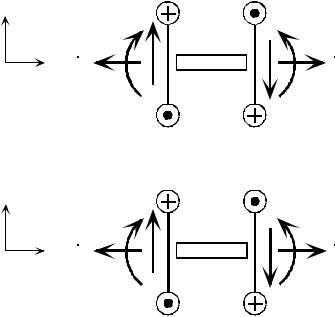
На рис. 2.2 и 2.3 в сечениях, соответствующих отброшенной правой части стержня, изобразим введенные формулами (2.4), (2.5) положительные направле- ния ВСФ для плоскостей xOy и xOz. Однако, из равновесия правой части стержня (при отбрасывании левой его части) получим величины, отличающиеся от ВСФ знаком. Для того чтобы из равновесия правой части получить те же самые величи- ны, что и из равновесия левой части, в сопротивлении материалов (и во всей меха- нике ДТТ) и принимаются противоположные (разные) положительные направле- ния для неизвестных ВСФ при рассмотрении равновесия левой и правой части. Тогда знак еще раз поменяется, вследствие чего из равновесия и левой и правой части (уравнения (2.2) – (2.3)) будут получаться одни и те же неизвестные величи- ны. Положительные направления ВСФ при отбрасывании левой части также изо-

- 24 -

риалов: используется в большинстве учебников и учебных пособий по данной дисциплине, к нему привыкли инженеры. Следует иметь в виду, что данное правило знаков, как будет видно, не согла- совано с правилом знаков для напряжений (величин, характеризующих внутренние силы в точках ДТТ), что ведет к появлению не вполне логичных знаков минус в ряде соотношений. Выбрав иное правило знаков, можно было бы избавиться от них.

4. Принятое правило знаков не увязано и с векторным представлением моментов, со- гласно которому требуется, чтобы положительные составляющие моментов создавали вра- щение относительно своих осей по правилу правого винта. Чтобы перейти к векторному представлению указанных величин, нужно убрать знак минус в формулах перехода (2.5). Но тогда надо принять разные правила знаков для плоскостей xOy и xOz, что, видимо, еще менее удобно.

В ходе вывода соотношений для определения ВСФ в стержне использо- вался метод рассуждений, применяемый далее всюду в данном курсе, да во всей механике ДТТ и называемый методом сечений. Согласно этому методу для определения ВСФ в данном сечении необходимо:

1.Разрезать мысленно стержень поперечным сечением в точке оси стерж- ня, где мы хотим определить ВСФ.

2.Отбросить одну из частей стержня. Отбрасывать удобнее часть, где больше сил. Важно лишь, чтобы внешние силы, действующие на остающуюся часть стержня, были известны.

3.Заменить действие отброшенной части неизвестными ВСФ, которые прикладываются в рассматриваемом сечении в положительном направлении, определяемом специальным правилом знаков для ВСФ.

4.Записать уравнения равновесия оставшейся (рассматриваемой) части стержня, определить из них ВСФ в сечении.

Для облегчения запоминания этого алгоритма метод сечений называют ме- тодом РОЗУ по первым буквам слов: разрезать, отбросить, заменить, уравнения.

При проверке прочности необходимо знать эпюры ВСФ во всех сечениях конструкции. ВСФ, меняющиеся вдоль оси стержня, будут функциями про- дольной координаты x. Графики этих функций, построенные на оси стержня, называются эпюрами ВСФ. Эпюры удобны тем, что дают наглядную информа- цию о ВСФ в различных поперечных сечениях балки. На эпюрах не изобража- ют оси координат. Эпюры строят с соблюдением масштаба, их принято штри- ховать перпендикулярно продольной оси стержня, указывать на них знак и ха- рактерные значения ВСФ.

- 25 -

Тема №3. Построение эпюр внутренних силовых факторов в стержне

Алгоритм построения эпюр ВСФ в стержне

Порядок действий (алгоритм) при построении эпюр ВСФ включает в себя следующие этапы.

1. Определить реакции опор методами теоретической механики.

Замечание. Данный пункт можно не выполнять для консольных стержней, если рассматривать равновесие части стержня, не содержащей опору.

2. Разбить стержень на участки. Границами участков следует считать а) начало и конец стержня; б) точки приложения сосредоточенных сил и мо- ментов; в) начало и конец распределенной нагрузки, изменяющейся по одному закону.

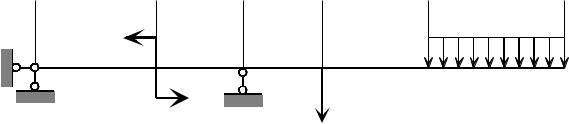
Например, в случае балки, изображенной на рис. 3.1, таких участков бу- дет пять. Точка С на рисунке также является границей участков, поскольку в этой точке приложена сосредоточенная сила опорной реакции.

Рис. 3.1

Замечание. Необходимость построения эпюр отдельно по участкам обусловле- на тем, что затруднительно написать единое соотношение для искомого ВСФ, спра- ведливое для всей длины стержня. На каждом участке, как увидим, для данного ВСФ получается свое аналитическое соотношение.

3. Применить метод сечений для каждого отдельного участка стержня и получить из уравнений равновесия аналитические выражения для ВСФ.

Замечания.

1.При записи уравнений равновесия после указания направления искомых ВСФ можно пользоваться как общей для всего стержня системой координат, так и любыми другими, например, локальными системами координат для каждого отдельного участ- ка. Это обусловлено тем, что условия равновесия выполняются для всех систем коор- динат, и если направление сил задано, то результат получится одинаковый для всех систем координат.

2.Рассматривается равновесие всей конструкции по одну сторону от сечения, а не только части участка, в пределах которого выбрано сечение. Это очевидно из само-

- 26 -

го метода сечений, согласно которому конструкция делится сечением на две части, а затем рассматривается равновесие одной из частей в целом.

4. Составить таблицы характерных значений эпюр на каждом участке.

Замечание. Данный пункт необходимо выполнять только в случае, если анали- тические выражения для ВСФ оказываются достаточно сложными.

5.Используя полученные аналитические выражения и таблицы значений, построить в некотором масштабе, обеспечивающем удобное прочтение, эпюры ВСФ.

Схему конструкции с нагрузкой и эпюры следует изображать друг под другом на отдельном листе.

6.Проверить правильность построения эпюр по соответствующим прави-

лам.

Примеры построения эпюр можно найти в пособии по построению эпюр [2, 3].

Дифференциальные уравнения равновесия участка стержня беско-

нечно малой длины

Рассмотрим брус под нагрузкой, находящийся в равновесии. Для просто- ты рассматривается прямой брус (стержень).

пределах выделенной части стержня сосредоточенных силовых факторов нет, поскольку в зоне их действия дифференциальные зависимости нарушаются. На рис. 3.2 изображены все внешние и внутренние силовые факторы для плоско- сти x0y, которые могут действовать на выделенную часть стержня в плоской задаче.

Неизвестные внутренние силы и моменты для поперечного сечения в точке X + считаем положительными. Тогда для сечения X те же силы и момен- ты, по закону Ньютона о действии и противодействии, следует направлять в противоположные стороны, поскольку в точке X + – это действие правой части

- 27 -

на левую, а в точке X левой части стержня на правую почти в том же сечении. Если бы сечения X и X + совпадали, то модули силовых факторов были бы равны. В случае непрерывной задачи для бесконечно близких сечений на рас- стоянии dx модули будут отличаться на бесконечно малую величину. Но по- скольку нами приняты для площадки в точке X обратные направления поло- жительных силовых факторов, это будут значения тех же функций, что и для сечения в точке X + , поэтому можно записать для непрерывной дифференци-

руемой задачи

Переменность погонных величин по координате х можно не учитывать, по- скольку это приводит к появлению малых слагаемых в уравнениях равновесия, которые все равно в дальнейшем придется отбросить.

Названные внутренние и внешние нагрузки могут в общем случае дейст- вовать в плоской задаче на элемент стержня длиной dx. Они должны находить- ся в равновесии, а потому выполняются три независимых уравнения равнове-

Моментное уравнение (3.4) может быть записано относительно любой точки. Выбрана точка X + на оси стержня (рис. 3.2), поскольку форма уравне- ния в этом случае наиболее проста. Пренебрегая в соотношении (3.4) слагае- мым, содержащим квадрат дифференциала, как бесконечно малым (более вы- сокого порядка малости по сравнению с другими слагаемыми), из уравнений

(3.2) – (3.4) получим

Соотношения (3.5) – (3.7) уже представляют собой дифференциальные уравнения равновесия элемента стержня бесконечно малой длины. Физический смысл слагаемых, входящих в эти соотношения, очевиден: это – приращения соответствующих величин на длине элемента. Обычно, однако, эти уравнения

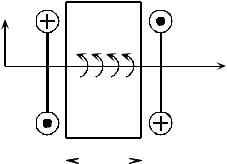
Вновь рассмотрим тот же бесконечно короткий элемент (рис. 3.3), но отобразим на рисунке только силовые факторы, создающие вращение относи- тельно оси x (не показаны на рис. 3.2, чтобы не перегружать изображение).

Аналогично предыдущему запишем условие равновесия моментов отно-

В результате получается следующая система дифференциальных уравне- ний равновесия элемента стержня бесконечно малой длины (объединены урав-

нения (3.8), (3.10) – (3.12)):

Уравнений, конечно, получается шесть, по числу степеней свободы абсолютно твердого тела в пространстве: три уравнения проекций на оси координат и три моментных уравнения. Несоответствия в знаках для уравнений проекций сил

обусловлены несовершенством традиционного правила знаков сопротивления материалов, несоответствия в знаках моментных уравнений – более серьезны- ми причинами, о которых говорилось ранее.

- 29 -

Распределенные моменты my и mz в практических приложениях встре- чаются редко. Поэтому при использовании для плоской задачи обозначений

причем уравнения (3.16) относятся к задаче изгиба стержня. Последние соот-

ношения приобрели форму простых дифференциальных зависимостей между интенсивностью изгибающей нагрузки q перерезывающей силой Q и изгибаю- щим моментом M.

Проверка правильности построения эпюр

Мы часто говорим, что людям свойственно ошибаться. Но лучше всего это знают те, кто составлял большие программы для вычислительных машин. Особенность этой работы в том, что в программе не должно быть ни одной ошибки, иначе программа работать не будет. Программисты хорошо знают, что в новой программе, текст которой больше одной страницы, непременно есть ошибка, причем у человека любой, даже самой высокой квалификации. И пе- ред тем как программа начнет работать, ее надо отлаживать.

Знают об этом, конечно, не только программисты, но и профессионалы- расчетчики. В практике расчетных бригад конструкторских бюро сложные рас- четные работы часто поручали вести двум разным людям (или разным брига- дам) параллельно, а полученные результаты сверяли. Результату можно дове- рять еще в большей степени, если он получен разными способами.

Таким образом, длинные последовательные расчеты, в том числе и по- строение эпюр ВСФ, надо тщательно проверять (расчет этот не слишком слож- ный, но студенты делают его впервые, что, конечно, увеличивает вероятность ошибок).

При построении эпюр не используется значительная часть информации о решении, которой удобно воспользоваться для проверки. Прежде всего это дифференциальные уравнения равновесия (дифференциальные зависимости). Одна группа правил проверки основана на этих уравнениях и на геометриче- ском смысле производной. Другая группа правил проверки основана на урав- нениях равновесия тела в целом и значительных его частей, т.е. на уравнениях равновесия в интегральной форме.

Правила проверки эпюр можно прочесть в пособии по построению эпюр [2].