
Lectures part1
.pdf- 61 -
Вместе соотношения (5.10), (5.11) образуют разрешимую систему уравнений. Эта система уравнений очень проста, она допускает разные пути решения. Выше мы ее решали следующим образом. Сначала при построении эпю-
ры N(x) интегрировали первое из уравнений (5.10) с использованием второго
граничного условия (5.11). Затем, из второго уравнения (5.10) нашли ε, после чего, интегрируя четвёртое из уравнений (5.10), нашли u.
Можно эту систему решать и по-другому, вначале записать силу в сече-
нии через перемещение |
|
||
N = EF |
du |
. |
(5.12) |
|
|||
|
dx |
|
|
Заметим, что полученное соотношение является обобщением соотношения, вы- текающего из равенства (4.9)
N = EF |
u(x) |
, |
(5.13) |
|
x |
||||
|
|
|
||
которое справедливо для стержня, растянутого силой на конце. |
|
|||
Подставив (5.12) в уравнение равновесия и приняв, что EF = const , при- дём к дифференциальному уравнению второго порядка относительно переме-
щений
EF |
d 2u |
= −qx . |
(5.14) |
|
dx2 |
||||
|
|
|
Известно, что для решения дифференциального уравнения второго порядка требуется два граничных условия. Столько граничных условий мы и имеем, но второе граничное условие следует переписать для осевого перемещения:
u(x = x A ) = 0 , EF du |
|
= P . |
(5.15) |
||
dx |
|
x=xB |
|
) |
|
|
|
|
|||
В итоге получаем замкнутую дифференциальную задачу для функции u x |
, ко- |
||||
|
( |
|
|
||
торая в данном случае легко решается. Затем по функции u(x) можно найти все
прочие величины задачи.
Последовательность действий, когда вначале находятся перемещения, представляет собой один из общих путей решения задач механики деформи- руемых тел – решение в перемещениях. Первый же из рассмотренных путей решения применим прежде всего к простым системам уравнений для брусьев, которые рассматриваются в сопротивлении материалов.
- 62 -
ОСНОВНЫЕ СООТНОШЕНИЯ ТЕОРИИ УПРУГОСТИ
Тема №6. Напряженное состояние в точке твердого тела. Дифференци-
альные уравнения равновесия
|
Напряженное состояние в точке твердого тела |
|||
|
q |
|
Экспериментальных и теоре- |
|
y |
|
А |
|
тических данных, которые получе- |
|
|
|
ны при изучении растяжения, доста- |
|
|
|
|
|
точно для того, чтобы получить об- |
|
|
|
|
|
|
|
|
|
щие соотношения теории упруго- |
|
|
|
||
z |
|
x |
|
сти. Затем из них можно будет по- |
|
|
лучать частные результаты. Кроме |
||
|
Рис. 6.1 |
|
||
|
|
|
того, почти все общие соотношения |
|
потребуются в нашем курсе, хотя в нем и изучаются в основном задачи для тел частного вида, для стержней.
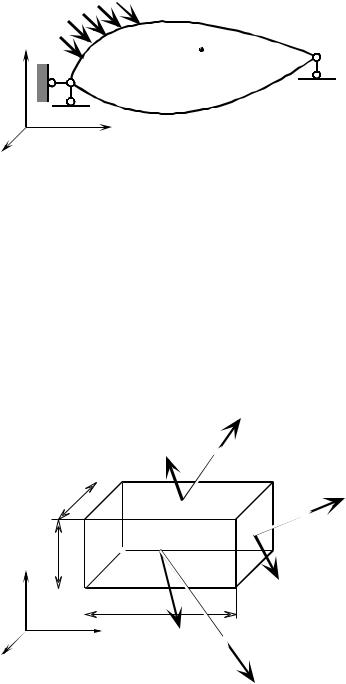
Рассматривается твердое тело под действием произвольной внешней на- грузки (рис. 6.1). Пусть само тело и все его части находятся в равновесии. От- несем тело к прямоугольной системе декартовых координат x, y, z. Вырежем мысленно из тела по методу сечений (шестью последовательными сечениями) бесконечно малый прямоугольный параллелепипед со сторонами dx, dy, dz вблизи произвольной точки А так, чтобы грани были перпендикулярны осям x, y, z декартовых координат (рис. 6.2).
|
|
|
r |
|
|
|
|
r |
Nz |
|
|
|
|
Mz |
r |
|
|
|
|
σ z |
r |
||
|
|
|
r |
Ny |
|
dx |
|||||
σ y |
|
||||
dz |
A |
r |
|
z |
|||
|
My |
|
|
|
dy |
|
|
O |
|
r |
r |
|
|
|
|
||||
y |
Mx |
|
|||
x |
σ |
x r |
|||
|
|
|
|
|
Nx |
|
|
|
Рис. 6.2 |
|
|
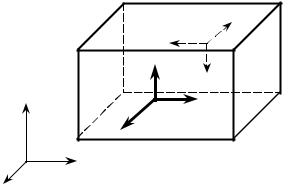
Каждая грань представляет собой бесконечно малую пло- щадку. По граням выделенного параллелепипеда будут действо- вать система сил со стороны от-
брошенного остального тела в каждой точке грани. Известно,
что система сил приводится к силе и моменту. Последний зави- сит от выбора точки приведения. Пометим векторы силы и момен- та индексом, указывающим ось,
которой перпендикулярна данная

- 63 -
площадка. Например, для бесконечно малой площадки со сторонами dy и dz сила и момент также бесконечно малы и обозначены на рисунке N x и M x .
Если каждая пара материальных точек соседних сечений воздействуют друг на друга только силой, но не моментом, то суммарный момент на малой площадке (например Mx , момент на площадке перпендикулярной оси x) будет вычисляться как сумма произведений силы, действующей на материальную точку, на бесконечно малое плечо, не превосходящее размера площадки (точка приведения выбирается внутри площадки). В этом случае очевидно, что мо- мент Mx будет величиной следующего порядка малости по сравнению с силой. И тогда моментами Mx , M y , Mz (рис. 6.2) внутренних сил на малых площад-
ках пренебрегают.
Только если каждая пара материальных точек соседних сечений взаимо- действует не только с силой, но и с моментом, то суммарные моменты окажут- ся того же порядка малости, что и силы. Тогда их следует учитывать, но это необходимо делать только в особых случаях, которые не рассматриваются в классической теории упругости. Не рассматриваются они и в данном курсе.
Выше уже говорилось, напряжением называется давление между слоями материала, поэтому вектор напряжения вводится (определяется), как и вектор давления на поверхности. Разделив вектор силы, например N x , на площадь грани, получаем вектор напряжения на площадке, направленный также, как
вектор силы
|
r |
|
|
= N x |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
(6.1) |
|
|
σ |
x |
|
dydz |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
σzz |
= σz |
|
Поскольку размеры пло- |
||||||||||
|
|
|
|
σ zx = τzx |
|
|
|
σzy = τzy |
|
щадки |
предполагается |
бес- |
|||||||||
|
|
|
|
|
|
||||||||||||||||
σxz = τxz |
|
|
|
|
|
|
|
|
|
σyz |
= τyz |
конечно малыми, предельный |
|||||||||
|
|
|
|
|
|
|
|
|
переход считается уже вы- |
||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
σ yy |
= σ y |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
полненным. Вектор напряже- |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ния также помечен индексом, |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
σyx = τyx |
указывающим |
ось, которой |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
перпендикулярно выбранное |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сечение. |
На |
координатных |
|
|
|
|
|
|
|
|
|
|
|
|
σxy = τxy |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
площадках получаются |
три |
||||||||
x |
|
y σ xx |
= σ x |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
вектора |
|
напряжений |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Рис. 6.3 |
|
σx , σ y , σz |
|
|
||||||||
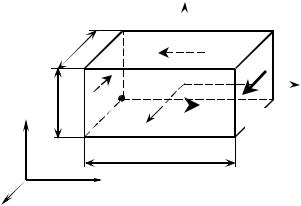
Разложив векторы напряжений на составляющие:
|
σx {σxx ,σxy ,σxz }, |
|
- 64 - |
|
|
|
|
|
|
|
|
|
|
|
|
|
σ y {σyx ,σyy ,σyz }, |
|
|
|
|
|
(6.2) |
|
σz {σzx , σzy , σzz } , |
|
|
|
|
|
|
получим сводку напряжений на координатных площадках (всего их девять). |
|||||||
Именно так обозначаются компоненты напряжений в математической литера- |
|||||||
туре. |
Из рис. 6.3 нетрудно видеть, что напряжения со смешанными индексами |
||||||
|
|||||||
представляют собой касательные напряжения. В технической литературе их |
|||||||
обычно обозначают буквой τ, а одинаковый индекс у нормальных напряжений |
|||||||
не повторяют. Запись векторов напряжений и их составляющих приобретает |
|||||||
тогда следующий вид |
|
|
|
|
|
|
|
|
σx {σx ,τxy ,τxz }, |
|
|
|
|
|
|
|
σ y { τyx ,σy ,τyz }, |
|
|
|
|
|
(6.3) |
|
σz { τzx , τzy , σz }. |
|
|
|
|
|
|
|
|
σx |
Как мы видим, первый индекс |
||||
|
τxy |
касательного |
напряжения |
указывает |
|||
|
τ+xz |
|
ось, которой перпендикулярна пло- |
||||
|
τxz |
щадка с касательным напряжением, |
|||||
z |
|
второй индекс – направление каса- |
|||||
|
τ+xy |
тельного напряжения |
|
|
|||
0 |
σ+ |
|
Векторы напряжений действуют в |
||||
|
общем случае на все шесть граней бес- |
||||||
|
x |
|
|||||
x |
y |
|
конечно |
малого |
параллелепипеда. |
||
|
Рис. 6.4 |
|
(рис. 6.2). Когда это необходимо, будем |
||||
|
|
отмечать напряжения на площадках, у |
|||||
|
|
|
|||||
которых внешняя нормаль совпадает с направлением соответствующей оси коорди- |
|||||||
нат, крестиком (плюсом), как это сделано на рис. 6.4, у таких же напряжений на |
|||||||
противоположных площадках этого знака ставить не будем. (Изображены положи- |
|||||||
тельные напряжения только на двух противоположных гранях, чтобы не загромож- |
|||||||
дать рисунок). Величины без верхнего индекса плюс и с ним, |
например: σx и |
||||||
σ+x ,– это два значения одной и той же функции, взятые в соседних точках (на |
|||||||
соседних гранях). Они получаются при проведении бесконечно близких сече- |
|||||||
ний, но отбрасывается в одном случае левая, а в другом случае правая часть |
|||||||
тела (относительно начала координат). И по закону Ньютона они были бы рав- |
|||||||
ны по величине, если бы сечение проходило через одну и ту же плоскость. В |
|||||||
данном же случае величины этих напряжений отличаются на бесконечно ма- |
|||||||
лую величину. |
|
|
|
|
|
|
|
- 65 -
По закону Ньютона они должны были бы отличаться знаком, но в меха-
нике деформируемого твердого тела принимаются обратные положительные направления для отрицательных площадок, в результате эти значения в полной мере оказываются значениями одной и той же функции. Так было и при рас- смотрении бесконечно короткого участка балки при выводе дифференциаль- ных уравнений равновесия стержня.
Таким образом, вблизи точки нагруженного тела действуют много раз- ных напряжений. Эти напряжения называют параметрами напряженного со- стояния в точке твердого тела, а само это физическое явление называют на- пряженным состоянием в точке. На координатных площадках их девять (три вектора напряжений), но напряжения действуют и на любых других площад- ках, проходящих через рассматриваемую точку. Очевидно, что напряжённое состояние около точки, представляет собой весьма сложное явление.
Еще раз подчеркнем, что напряжение – это обобщенное давление, кото- рое возникает, например, и на поверхности контакта двух твердых тел при уче- те сил трения. Отличие в том, что давление действует на поверхности твердых тел, а напряжениями называют величины, действующие внутри твердого тела. Есть еще отличие в правилах знаков для напряжений и давлений, в остальном эти понятия совпадают.
Уравнения равновесия бесконечно малого элемента трехмерного тела
1. Закон парности касательных напряжений
|
|
|
|
|
|
|
|
|
|
z1 |
|
|
|
|
Поскольку все тело находится в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
dx |
|
τxy |
|
|
|
|
|
|
равновесии, то и любая его часть тоже в |
|||||
|
|
|
|
|
|
|
|
равновесии, в том числе и бесконечно |
|||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y1 малый элемент этого тела. В трехмер- |
|
dz |
|
τyx A |
|
ц. т. |
τ+ |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
τ+yx |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
ном пространстве он должен удовлетво- |
|||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
x |
|
|
|
|
|
|
рять шести уравнениям равновесия. |
|||||
z |
|
|
|
|
1 |
|
|
xy |
|
|
|
|
|||
|
|
|
|
|
dy |
|
|
|
|
|
Составим сначала три моментных |
||||
O |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
уравнения. Они могут быть записаны |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
относительно различных осей. Выберем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Рис. 6.5 |
|
|
|
|
|
для записи уравнений равновесия оси |
|||||||
|
|
|
|
|
|
|
x1 , y1 , z1, параллельные осям x, y, z и |
||||||||
проходящие через центр тяжести элемента (рис. 6.5). Начнем с уравнения мо- ментов относительно оси z1 .
Изобразим на рис. 6.5 только те напряжения, которые дадут момент от- носительно оси z1 . Нетрудно видеть, что компоненты напряжений, действую-
щие на площадках, перпендикулярных оси z1 , момента не дают, поскольку σz
- 66 -
параллельно оси z1, а τzx и τzy могут дать момент относительно этой оси,
только если учесть их переменность. Но это приведёт к появлению малых сла- гаемых в уравнении равновесия, и эти малые слагаемые всё равно придётся от- бросить. По тем же причинам не дают момента и напряжения на боковых пло- щадках, перпендикулярных осям x1 и y1 , кроме указанных на рисунке каса-
тельных напряжений τ+xy ,τ+yx ,τxy ,τ yx .
Запишем теперь моментное уравнение равновесия относительно оси z1 .
Умножая соответствующее напряжение на площадь грани, по которой оно дей- ствует, получаем силу, которую затем умножаем на плечо относительно оси z1 .
Суммируя моменты от различных напряжений, получим: |
|
|
|||||
åM z |
|
= τxydydz dx |
+ τ+xy dydz dx |
− τyxdxdz dy |
− τ+yxdxdz dy |
= 0 . |
(6.4) |
|
1 |
2 |
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
От объемной нагрузки момент не записываем, поскольку объёмная сила
приложена в центре тяжести элемента и момента относительно этой точки дать не может.
На величину 0,5dxdydz равенство (6.4) можно сократить.
Выразим величины с индексом «+» через те же величины без этого ин- декса. Возьмем для примера напряжение τxy . Если на грани с отрицательной
нормалью действует τxy , то на одноименной площадке с положительной нор- малью действует τ+xy = τxy + ∂x τxy , несколько измененное значение, так как τ+xy взято в сечении, бесконечно близком к первому. Через ∂xτxy обозначен так на-
зываемый частный дифференциал τxy |
при смещении на величину dx вдоль оси |
||||||||||||
x. Можно использовать и другую форму записи этого дифференциала: |
|
||||||||||||
|
∂xτxy = |
|
∂τxy |
dx , |
|
|
|
(6.5) |
|||||
|
|
|
|
|
|
|
|||||||
|
∂τxy |
|
|
∂x |
|
|
|
|
|||||
где |
– частная производная функции τxy , поэтому |
|
|||||||||||
∂x |
|
||||||||||||
|
|
|
|
∂τxy |
|
|
|
|
|
|
|
||
|
τ+xy = τxy + |
dx . |
|
|
|
(6.6) |
|||||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
∂x |
|
|
|
|
|||
|
Подставив это равенство и аналогичное для τ+yx , в моментное уравнение |
||||||||||||
равновесия, получим |
|
|
|
|
|||||||||
|
åM z |
= τxy + τxy + |
∂τxy |
dx − τyx |
− τyx − |
∂τyx |
dx = 0 . |
(6.7) |
|||||
|
|
|
|||||||||||
|
|
1 |
|
|
|
|
|
∂x |
|
∂y |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В это соотношение вместе с дифференциалами функций входят и сами функции. В этом случае дифференциалами следует пренебречь, в результате
чего придем к равенству
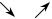
- 67 - |
|
τxy − τyx = 0 . |
(6.8) |
Аналогично можно получить и два других соотношения, которые нахо- |
|
дятся из моментных уравнений равновесия относительно осей x1 и |
y1 .Таким |
образом |
|
τxy = τyx , τyz = τzy , τzx = τxz , |
(6.9) |
которые, однако, проще записать формально с помощью циклической переста- новки индексов:
x  z
z
y |
(6.10) |
|
|
Соотношения (6.9) выражают закон парности (или взаимности) каса- |
|
тельных напряжений. Формулируется этот закон следующим образом. |
|
На каждых двух взаимно перпендикулярных площадках, проходящих че- |
|
рез данную точку тела, компоненты касательных напряжений, перпендику- лярные к линии пересечения этих площадок, равны по величине и направлены оба либо к линии пересечения, либо от нее.
Закон доказан для площадок, связанных с системой координат, но сама система координат была выбрана произвольно, поэтому для произвольной па- ры взаимно перпендикулярных площадок всегда можно указать систему коор- динат, для которой справедливы проведенные рассуждения.
Таким образом, напряженное состояние в окрестности точки для выбран-
ной системы декартовых координат описывается только шестью компонентами
напряжения |
|
σx ,σy ,σz ,τxy ,τyz ,τzx , |
(6.11) |
а таблица напряжений (6.3) оказывается симметричной относительно главной диагонали.
Итак, моментные уравнения равновесия бесконечно малого параллелепи- педа приводят к закону парности касательных напряжений.
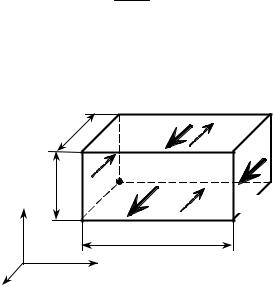
2. Дифференциальные уравнения равновесия бесконечно малого паралле-
лепипеда Рассмотрим теперь три уравнения равновесия того же параллелепипеда
(рис. 6.6) в проекциях на оси. Изобразим на параллелепипеде только напряжения, дающие проекцию на ось x. Умножая напряжения на площади площадок, по кото- рым они действуют, получаем силы, приложенные к параллелепипеду и дейст- вующие в направлении оси х. Кроме них в направлении оси х может действовать составляющая объемной силы, которая, конечно, вычисляется умножением соот- ветствующей проекции удельной объемной силы (γ x ) на объем параллелепипеда.
|
|
|
|
|
|
|
- 68 - |
|
|
|
Силы должны удовлетворять уравнению равновесия для этой оси: |
|
|||||||||
s+x dydz - sxdxdz + t+yxdxdz - tyxdxdz + t+zxdxdy - tzx dxdy + rx dxdydz = 0. |
(6.12) |
|||||||||
Выражая |
снова напряжения с индексом «+» через |
напряжения без этого |
||||||||
индекса, получим: |
|
|
|
|
|
|||||
|
æ |
¶s |
x |
|
ö |
|
|
|
|
|
|
çsx + |
|
|
dx÷dydz - sxdxdz + |
|
|
|
|||
|
è |
¶x |
|
ø |
|
|
|
|
||
|
æ |
|
¶tyx |
ö |
|
|
|
|
||
|
ç |
+ |
|
|
|
÷ |
- tyxdxdz + |
|
|
(6.13) |
|
+ çtyx |
|
¶y |
dy÷dxdz |
|
|
||||
|
è |
|
|
ø |
|
|
|
|
||
|
æ |
+ |
¶t |
zx |
ö |
|
|
|
|
|
|
+ çtzx |
|
|
dz÷dxdy - tzxdxdy + rxdxdydz = 0 . |
|
|
||||
|
è |
|
|
¶z |
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда видно, что слагаемые с напряже- |
||
|
dx |
|
|
|
|
+ |
sx |
ниями взаимно уничтожаются (в отличие |
||
|
|
|
|
|
τzx |
|
от моментных уравнений) и уравнение |
|||
dz |
tyx |
|
|
|
τ |
|
записывается для приращений (частных |
|||
A |
|
zx t+yx |
дифференциалов |
напряжений). |
После |
|||||
z |
|
|
|
s+x |
сокращения на величину объема парал- |
|||||
|
|
|
|
|
|
dy |
|
|||
|
|
|
|
|
|
|
лелепипеда приходим к уравнению рав- |
|||
O |
|
|
|
|
|
|
|
|||
y |
|
|
|
|
|
новесия. Аналогичным путем (проекти- |
||||
x |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
руя силы на оси y и z) или циклической |
|||
|
|
|
Рис. 6.6 |
|
||||||
|
|
|
|
перестановкой символов получаем еще |
||||||
два дифференциальных уравнения равновесия бесконечно малого элемента трехмерного тела:
¶s |
x |
+ |
|
∂τyx |
+ |
|
¶t |
zx |
+ rx = 0, |
|
||||
|
|
¶y |
|
|
|
|||||||||
¶x |
|
|
|
|
¶z |
|
|
|||||||
∂σ y |
+ |
|
∂τzy |
+ |
|
∂τxy |
+ ry = 0 , |
(6.14) |
||||||
¶y |
|
¶z |
|
¶x |
||||||||||
|
|
|
|
|
|
|||||||||
¶s |
z |
|
+ |
¶t |
xz |
|
+ |
∂τyz |
|
+ rz = 0. |
|
|||
¶z |
|
¶x |
|
¶y |
|
|||||||||
|
|
|
|
|
|
|||||||||
В эти уравнения входят шесть неизвестных величин, а уравнений только три. Исходя из одних уравнений равновесия задача не решается. Такие задачи называются статически неопределимыми. О них подробнее поговорим позже. А здесь просто отметим, что уравнения теории упругости внутренне статически неопределимы.
- 69 -
Тема №7. Напряженное состояние в точке твердого тела. Напряженное
состояние на площадках различной ориентации
Виды напряженного состояния в точке деформируемого твердого тела
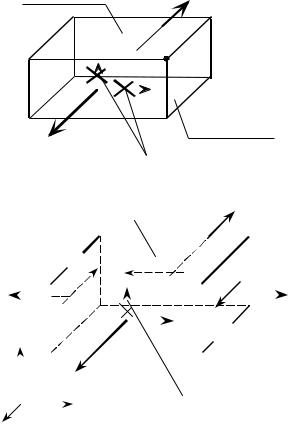
Различают три вида напряженных состояний, которые могут иметь место вблизи материальной точки твердого тела.
|
|
σ = 0, τ = 0 |
|
|
|
|
|
|
|
|
|
σ |
1. Напряженное состояние |
в |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
точке называется одноосным, если че- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рез данную точку тела можно провес- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
ти две взаимно перпендикулярные плос- |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кости, на которых вблизи данной точ- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ки нет напряжений. |
|
|
|
|
|
σ+ |
|
|
|
|
|
|
τ = 0 |
σ = 0, τ = 0 |
Допустим, что вблизи произволь- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ной точки А нет напряжений на двух |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Рис. 7.1 |
|
|
|
|
|
|
|
взаимно перпендикулярных площадках |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(σ = 0 и τ = 0 ) (рис.7.1). В этом случае |
||||||||
|
|
|
σ = 0, τ = 0 |
|
|
|
|
σx |
||||||||||||||||
|
|
|
|
|
|
|
на третьей площадке возможно только |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
одно нормальное напряжение σ, а каса- |
|
|
|
|
|
|
τ |
|
|
τyx |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
xy |
|
|
|
|
|
|
|
тельное напряжение τ также будет ну- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
левым в силу закона парности каса- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
σy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ+y |
||||||
|
|
|
|
|
|
|
|
|
|
τ+xy |
|
|
|
тельных напряжений. |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
z |
|
|
|
|
|
|
|
|
|
|
|
|
τ+yx |
2. Напряженное состояние в точ- |
||||||||||
|
|
|
|
σ+x |
|
|
|
|
|
|
|
τ = 0 |
|
|
|
ке называется плоским или двухосным, |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
O |
|
|
|
|
|
|
|
|
|
|
|
|
если через неё можно провести только |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
одну плоскость, на которой вблизи дан- |
|||
x |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
Рис. 7.2 |
|
|
|
|
|
|
|
ной точки нет напряжений (σ = 0 |
и |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ = 0 ) (рис. 7.2). На рис. 7.2 произволь- |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ная система декартовых координат взята так, чтобы ось z была перпендикулярна плоскости без напряжений. В силу закона парности в данном случае на двух других координатных площадках будут действовать не все компоненты касательных на- пряжений. На них отличны от нуля только напряжения σ x , σ y , τxy = τ yx .
3. Напряженное состояние в точке называется трехосным или объем- ным, если через неё нельзя провести ни одной плоскости, на которой вблизи данной точки нет напряжений.
- 70 -
Одноосное напряженное состояние. Напряжения на наклонных площадках.
|
|
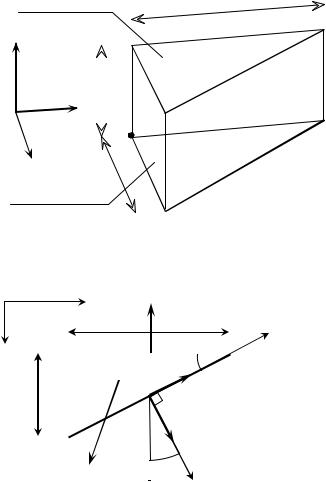
Допустим, что вблизи некоторой точки А в теле, находящемся в равнове- |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сии, |
действует |
одноосное |
напря- |
||||||
|
σ = 0, τ = 0 |
|
|
|
|
|
|
dy |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
женное состояние. Пусть, например, |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на гранях, перпендикулярных осям y |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и z, σ = 0 |
и |
τ = 0 |
(рис. 7.3). Такое |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
dz |
|
|
|
|
|
|
|
|
|
|
|
напряженное состояние, как извест- |
||||||||||||
O |
|
y |
|
A |
|
|
|
|
но, |
возникает, в частности, |
для то- |
||||||||||||||||
|
|
|
|
|
|
|
чек растянутого стержня. Вырежем |
||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
мысленно |
из |
тела |
вблизи |
точки А |
||||||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
бесконечно |
малую |
прямую тре- |
|||||||||
|
σ = 0, τ = 0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
угольную призму, две боковые гра- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
Рис. 7.3 |
|
|
|
|
ни которой перпендикулярны осям x |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и y, а нормаль к третьей, напряже- |
|||||||||
ние на которой будем определять, составляет угол α с осью x (рис. 7.4). |
|
||||||||||||||||||||||||||
|
|
|
y |
|
|
|
σx |
|
|
|
|
Введем новую систему координат |
|||||||||||||||
x |
|
A |
|
|
|
|
|
dy |
|
|
|
ξ и η, связанную с этой гранью так, как |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
η |
показано на рисунке. На грани АВ, со- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
α |
C |
гласно условию, напряжений не будет. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
τξη |
|
|
|
||||||||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
На грани |
ВС предположим |
наличие и |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
нормальных, и касательных напряжений |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
и установим их из уравнений равновесия |
||||||||||||||
|
|
B |
|
|
|
|
α ξ |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
ρ |
|
|
|
|
|
|
выделенного |
элемента |
|
относительно |
|||||||||||
|
|
|
|
|
|
|
Рис. 7.4 |
|
|
|
осей ξ и η, считая известными напря- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
жения |
σx |
на |
грани |
АС. |
Обозначим |
|||||
Fx = dxdz площадь грани |
АС, Fξ |
– площадь грани |
ВС, |
тогда |
Fx |
= Fξ cosα , |
|||||||||||||||||||||
ρξ - объемная сила в направлении оси ξ , например вес материала. Запишем уравнение равновесия относительно оси ξ :
åξi = σξ Fξ − σ x Fx cos α − ρξ |
dx |
Fξ cos α = 0 . |
(7.1) |
|
|||
2 |
|
|
|
Пренебрегая последним слагаемым с бесконечно малым множителем dx |
|||
по сравнению с остальными слагаемыми, получим |
|
||
σξ = σx cos2 α . |
(7.2) |
||
Здесь и далее не будем учитывать объемные силы при выводе формул для напряжений на наклонных площадках, так как во всех случаях ими можно пре-
