
Lectures part1
.pdf
- 151 -
следует определить площадь контакта тел Fк , вызывающих появление силы, и,
поделив на эту площадь величину приложенной силы, определяют среднее кон- тактное напряжение σy сред , т.е. напряжение смятия. Сравнивая полученное на-
пряжение с допускаемым на смятие, можно оценить возможность разрушения
от местных контактных напряжений
σy сред = σсм = P ≤ [σ]см . (13.17)
Fк
Влиянием этих напряжений на другие величины задачи при расчёте на смятие пренебрегают. Существуют и уточнённые методики учёта этих напря- жений.
|
|
Концентрация напряжений |
||
σx |
|
|
|
|
σx ном |
|
d |
σx спл |
|
Q |
|
|
b |
Q |
|
|
|
|
|
σx max |
|
|
|
|
y |
|
|
|
|
0 |
x |
|
|
|
|
σx ном |
Рис. 13.9 |
σx спл |
|
|
|
|||
|
0,5Q1 |
|
0,5Q |
|
|
|
|
|
1 |
|
0,5Q1 |
|
0,5Q1 |
|
y |
|
′ |
|
A |
|
A |
|
||
0 |
x |
B′ |
|
B |
|
|
|
Рис. 13.10 |
|
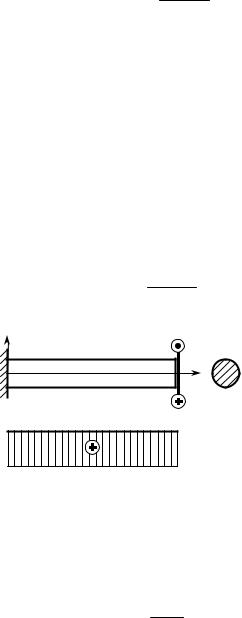
Напряжения в поперечном сечении листа, ослабленном отверстиями, как уже говорилось, будут отличаться от номи- нальных. Истинная картина распределе- ния напряжений по сечению с отвер- стиями выглядит примерно так, как пока- зано на рис. 13.9 (изображена часть лис- та, мысленно выделенная двумя сече- ниями поперек линии действия силы Q).
Перераспределение напряжений в зоне отверстия неизбежно должно происхо- дить, поскольку sx ном ¹ sx спл . Это пере-
распределение и приводит к появлению пиков напряжений σx по границам от-
верстий.
Действительно, мысленно выделим вблизи отверстия элемент листа, как по- казано на рис. 13.10. Ширину элемента возьмём такой, чтобы приложенная к элементу сила, являющаяся равнодейст- вующей напряжений, была равна Q1 –
силе, действующей на одну заклёпку. Силы, приложенные к половинам этого элемента, равны половинам силы Q1, но действовать они будут не по одной ли-
нии, и можно заметить, что элемент листа около отверстия нагружается так, что происходит изгиб, в результате чего края отверстия в поперечном сечении

- 152 -
(вблизи точек A и A′, B и B′) должны разойтись. Препятствовать такой дефор- мации должны бòльшие` нормальные напряжения σx по краю отверстия.
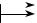
Около отверстия меняется и характер напряженного состояния: из одно- осного в данном случае оно превращается в плоское. Мысленно выделим оди- наковые «продольные волокна» с частью отверстия (рис. 13.11). Можно заме- тить, что такие «волокна» будут изгибаться в сторону отверстия из-за того, что растягивающая сила Q в ослабленном сечении «волокна» перестаёт быть осе-
вой. Препятствовать изгибу будут дополнительные нормальные напряжения σy , и напряженное состояние становится плоским. В общем случае концентра-
ция напряжений может сделать напряженное состояние и объёмным.
Картину распределения напряже-
Q |
Q |
Q




 Q
Q
σx спл |
σx спл |
y |
|
0 x
Рис. 13.11
ний около отверстий можно получить методами теории упругости или экспе- риментально. Поскольку номинальное напряжение σx ном представляет собой
среднее напряжение по сечению, а сумма сил от напряжений σx должна давать ту
же самую внешнюю нагрузку Q, значе- ние напряжения σx (рис. 13.9) будет
всюду несколько меньше номинального,
кроме небольшой зоны у края отверстия:
Q = σx ном Fослаб = òσxdF ,
Fослаб
тогда, если на части сечения напряжения больше средних (номинальных), то на остальной части они будут меньше средних.
Такое перераспределение напряжений и называется концентрацией на-
пряжений.
Важно отметить, что при уменьшении диаметра отверстия пик напряже- ния σx возрастает. Согласно решению теории упругости, в пределе при умень-
шении диаметра отверстия до нуля значение этого напряжения втрое превосхо- дит номинальное. Вводят так называемый теоретический коэффициент кон-
центрации напряжений по формуле
α = σx max .
кт σx ном
В указанном случае αкт = 3.
Концентраторами напряжений являются не только отверстия, но и тре- щины, раковины, инородные включения, канавки, выточки, входящие углы,
- 153 -
риски, царапины, переходы диаметров, сварные швы и т.д. Самые сильные концентраторы напряжений – трещины.
При проверке прочности конструкций из хрупких материалов концентра- цию напряжений необходимо учитывать. От больших нормальных растяги- вающих напряжений в них могут появиться трещины, которые быстро или даже мгновенно разрушат конструкцию. Однако для пластичных материалов концен- трация напряжений при однократном и постоянном нагружении не опасна. Она приводит к небольшим пластическим деформациям в зонах концентраторов, общего же разрушения конструкции при этом не происходит. Практически не меняется от концентрации напряжений и разрушающая нагрузка, поскольку перед разрушением в пластической зоне пики напряжений сглаживаются, все напряжения достигают значения предела текучести и дальше растут мало.
Только при многократно повторяющихся нагрузках концентрацию напряжений приходится учитывать и для пластичных материалов.
|
|
- 154 - |
Тема №14. КРУЧЕНИЕ СТЕРЖНЕЙ |
||
Основные гипотезы, принимаемые при кручении круглого стержня. |
||
В предыдущих темах рассмотрены уже три вида деформаций стержня: |
||
растяжение-сжатие, изгиб и сдвиг. Остался последний вид деформаций – |
||
кручение. Направим ось x как всегда вдоль линии центров тяжести сечений, |
||
т.е. вдоль оси симметрии стержня. Кручением называется вид деформаций |
||
стержня, вызванный моментами относительно его продольной оси. Крутящий |
||
момент будем обозначать |
M x (x) |
или Mкр (x). Изучение вопроса естественно |
начинать с простейших задач. Таковой в данном случае является задача о кру- |
||
чении круглого стержня. Существует аналитическое решение этой задачи на |
||
основе соотношений теории упругости. Но здесь рассмотрим решение этой за- |
||
дачи непосредственно на основе эксперимента и введения гипотез (именно так |
||
оно впервые было получено). Заметим, что в технике стержень, передающий |
||
вращение и крутящий момент, называют валом. |
||
y |
|
Пусть прямой стержень имеет круг- |
x |
|
лое поперечное сечение. Будем считать, |
|
что левое сечение стержня защемлено, а к |
|
y |
M x |
правому его концу прикладывается внеш- |
|
|
ний крутящий момент M x (рис. 14.1). До |
x |
|
приложения нагрузки на его поверхности |
|
нанесена равномерная сетка взаимно пер- |
|
dx |
|
|
Рис. 14.1 |
|
пендикулярных линий, аналогично случа- |
|
ям растяжения-сжатия и изгиба. На пра- |
|
вом торце тоже нанесём сетку линий, как показано на рисунке. О характере де- |
||
формаций после приложения момента судим по изменениям этой сетки. |
||
При малых перемещениях и деформациях заключаем следующее: |
||
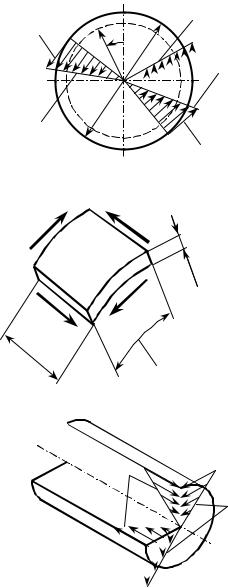
1)следы поперечных сечений остаются окружностями;
2)все прямые углы между линиями сетки изменяются одинаково (на один и тот же угол);
3)сетка линий на торце стержня не деформируется;
4)длина стержня почти не меняется;
5)ось стержня остаётся прямой линией.
Заметим, что пространственные кривые, получающиеся из образующих, представляют собой винтовые линии.
На основании этих наблюдений была сформулирована для данного случая гипотеза плоских сечений (использовалась и для других видов деформации

- 155 -
стержня), а также другие гипотезы:
1)материальные точки стержня, до деформации находившиеся в одной плоскости поперечного сечения, после деформации остаются в одной плоско- сти, и эта плоскость остаётся перпендикулярной продольной оси стержня;
2)поперечное сечение не деформируется в своей плоскости;
3)ось стержня остаётся прямой линией и не меняет своей длины.
Другими словами, считаем, что поперечные сечения ведут себя как жест-
кие диски, насаженные на недеформирующуюся ось стержня.
Гипотезы являются кинематическими (или геометрическими), поскольку
в них говорится только об особенностях деформированного состояния и ничего об усилиях.
|
|
Часть этих результатов экспери- |
|
γ |
|
мента можно было ожидать: в условиях |
|
|
|||
|
|
осевой симметрии ось стержня должна |
|
|
|
||
Рис. 14.2 |
оставаться прямой; образующая при кру- |
||
чении несколько меняет свою длину, но |
|||
|
|
||
при малых перемещениях и деформациях это отличие примерно такое же, как у гипотенузы треугольника с его большим катетом (рис. 14.2). Если угол между гипотенузой и катетом мал, то и указанное отличие очень малое.
Решение этой задачи на основе соотношений теории упругости показыва- ет, что все гипотезы выполняются точно, кроме, естественно, неизменности
длины стержня. Отметим ещё, что при больших` |
перемещениях и деформациях |
|||||||||
длина стержня уменьшается. |
|
|||||||||
|
|
|
|
Кинематические соотношения при кручении круглого стержня |
||||||
α |
|
|
|
|
|
|
|
|
Отнесём стержень к цилиндрической системе |
|
|
ϕ |
|
ϕ + dϕ |
координат x, r, α, в которой ось x снова направлена |
||||||
|
|
|||||||||
r |
|
a |
||||||||
|
вдоль оси стержня. Мысленно выделим из стержня |
|||||||||
|
a |
* |
|
|
|
|
||||
|
|
|
|
|
|
|
|
под нагрузкой двумя бесконечно близкими сечения- |
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
x |
|
C |
b |
* |
b |
|
|||
|
|
|
ми элемент длиной dx (рис. 14.1) и изобразим его с |
|||||||
|
|
C+ |
||||||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
необходимым искажением пропорций в увеличен- |
|||
|
|
|
|
|
|
|
|
|
ном масштабе (рис. 14.3). Обозначим углы поворота |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
dx |
|
|
|
r |
поперечных сечений |
стержня через ϕ(x), поворот |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
сечения в произвольной точке C оси стержня че- |
|||
|
|
|
|
|
|
|
|
|||
|
|
Рис. 14.3 |
рез ϕ. Поворот бесконечно близкого к нему сечения |
|||||||
|
|
|
|
|
|
|
|
|
в точке C + в непрерывной дифференцируемой зада- |
|
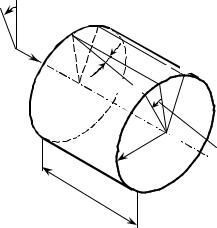
че можно записать, как и в других подобных случаях: ϕ(xC + ) = ϕ + dϕ .
- 156 -
Тогда правое сечение выделенного элемента повернется относительно левого на угол dϕ . Выбранная произвольно образующая поверхности цилиндра ab займет
α |
|
|
|
|
|
после деформации |
положение |
a*b* . |
В |
|
c* |
с |
|
|
|
плоскости сечения |
получается |
полярная |
|||
r |
|
|
|
|||||||
|
|
|
система координат r и α. Продольным ци- |
|||||||
0 |
x |
γxα |
|
* d′ |
d |
линдрическим сечением радиуса r выделим |
||||
d |
из первоначального |
элемента длиной |
dx |
|||||||
|
C |
|
||||||||
|
|
|
|
другой цилиндрический элемент меньшего |
||||||
|
|
|
|
|
|
|||||
|
|
|
|
C+ |
dϕ |
радиуса, но той же длины и рассмотрим его |
||||
|
|
|
r |
деформацию (рис. 14.4). Масштаб изобра- |
||||||
|
|
dx |
|
|
жения на рисунке ещё раз увеличен. |
|
||||
|
|
|
|
|
|
|||||
|
|
|
|
|
Произвольная образующая cd по- |
|||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
верхности элемента при деформации по- |
||||
|
Рис. 14.4 |
|
вернется и займет положение c*d* . Про- |
|||||||
|
|
|
|
|
|
ведём по поверхности вспомогательную |
||||
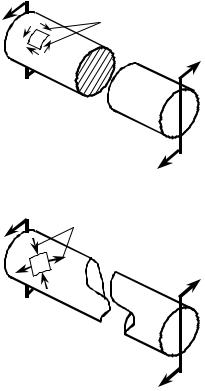
образующую c*d′. Прямой до деформации угол c*cd уменьшится в результате деформации на угол γ xα , который, по определению, является углом сдвига, но в
цилиндрической системе координат. Причем в силу гипотезы плоских сечений этот сдвиг однороден (постоянен) в окружном направлении.
В секторе C +d′d* дуга d′d* = rdϕ, в треугольнике c*d′d* приблизительно
та же дуга (при малых перемещениях и деформациях) запишется |
так: |
||
′ |
|
||
d d* = γ xαdx . Поэтому rdϕ = γ xαdx . Следовательно, получим: |
|
||
γxα = |
dϕ |
r . |
(14.1) |
|
|||
|
dx |
|
|
Нетрудно видеть, что другие линейные и угловые деформации в цилинд- |
|||
рической системе координат согласно принятым гипотезам равны нулю |
|
||
εx = εr = εα = γ xr = γrα = 0 . |
(14.2) |
||
Из перемещений отличным от нуля получится только перемещение в направле- нии угла α.
Соотношение упругости и формулы для определения напряжений при кручении круглого стержня
Деформация сдвига связана формулой закона Гука для сдвига (обобщен- ного закона Гука) с касательными напряжениями, поэтому с помощью форму- лы (14.1) получаем
τxα = Gγxα = G |
dϕ |
r . |
(14.3) |
|
|||
|
dx |
|
|
- 157 -
Входящая в эту формулу производная представляет собой угол закручивания, приходящийся на единицу длины в данной точке. Эту величину называют от- носительным углом закручивания (интенсивностью угла закручивания или по- гонным углом закручивания). Она представляет собой в общем случае функ-
цию продольной координаты x. Обозначим её так: |
|
|
|
||||||||||||||||||
ξ(x)= |
dϕ |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(14.4) |
|||
|
|
|
|
|
|
|
|||||||||||||||
|
|
dx |
|
|
|
Для каждого фиксированного сечения это |
|||||||||||||||
τxα max |
|
|
|
|
|
|
|
|
|
|
|
|
|
τxα |
|||||||
r |
α |
одно число, константа, поэтому формула |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τxα |
(14.3) позволяет судить о законе распреде- |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ления касательных напряжений по сече- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
D |
|
|
|
||||||||||||||||
|
|
|
|
|
нию, хотя определить сами значения каса- |
||||||||||||||||
τxα |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ |
тельных напряжений ещё невозможно, по- |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
скольку не знаем величину ξ(x). |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xα max |
|||||
|
|
Рис. 14.5 |
|
|
|
Касательные напряжение, как вид- |
|||||||||||||||
|
|
|
|
|
но из формулы (14.3), меняется по ли- |
||||||||||||||||
τxα |
|
|
|
ταx |
|
|
|
||||||||||||||
|
|
|
|
|
|
нейному закону по радиусу r и не меня- |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ется по |
окружной |
координате α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dr |
(рис. 14.5). |
Максимальное |
напряжение |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
достигается в сечении вблизи внешней |
|||||
|
|
|
|
|
τxα |
|
|
|
|||||||||||||
ταx |
|
|
|
|
|
|
поверхности |
стержня. |
Никаких других |
||||||||||||
|
|
|
|
|
|
|
|
rdϕ |
|
|
|
напряжений, кроме касательных τxα и |
|||||||||
dx |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
парных им ταx , на площадках цилиндри- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Рис. 14.6 |
|
|
|
ческой системы координат не возникает, |
|||||||||||||||
|
|
|
|
|
что следует из обобщенного закона Гука. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поскольку |
площадки |
цилиндрической |
|
|
|
|
ταx |
|
|
|
системы координат, как и декартовой, |
||||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τxα |
взаимно перпендикулярны, то, по опре- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
делению, напряжённое состояние в мате- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
риале является чистым сдвигом. На ма- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
лый прямоугольный элемент, мысленно |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вырезанной с поверхности элемента на |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Рис. 14.7 |
|
|
|
рис. 14.4 дополнительными |
сечениями, |
||||||||||||||
|
|
|
|
|
действуют только касательные напряже- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ния чистого сдвига (рис. 14.6). Распределение этих же напряжений внутри стержня иллюстрирует рис. 14.7.
Напомним, что на площадках, повёрнутых на 45° к площадкам сдвига (с максимальными касательными напряжениями), действуют только нормаль-
- 158 -
ные напряжения (равные касательным): одни на растяжение, другие на сжатие.
|
|
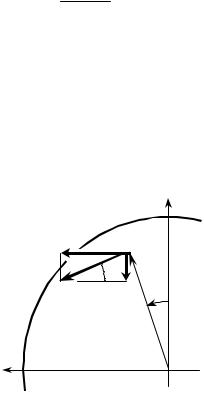
Такое распределение напряжений объяс- |
|||
τ |
|
няет характер разрушения различных ма- |
|||
Mкр |
|
териалов при кручении круглых стерж- |
|||
|
ней. |
Пластичные металлы срезаются по |
|||
Mкр |
|
поперечному сечению от действия наи- |
|||
|
больших |
касательных |
напряжений |
||
|
|
||||
|
|
(рис. 14.8). Хрупкие металлы разруша- |
|||
|
|
ются от отрыва в направлении наиболь- |
|||
Рис. 14.8 |
|
ших нормальных напряжений (рис. 14.9). |
|||
|
На рис. этих рисунках напряжения и на- |
||||
σ = τ |
|
||||
|
грузки изображены условно. Они дейст- |
||||
|
|
||||
|
|
вовали до разрушения. По ГОСТу харак- |
|||
|
Mкр |
тер разрушения металла при кручении |
|||
|
(срез или отрыв) считается его механиче- |
||||
Mкр |
|
||||
|
ской |
характеристикой. |
Анизотропная |
||
|
|
древесина (кругляк) при кручении вокруг |
|||
|
|
оси ствола растрескивается в направле- |
|||
Рис. 14.9 |
|
нии |
действия касательных напряжений |
||
|
ταx , |
поскольку дерево оказывается наи- |
|||
|
|
||||
менее прочным на данный вид напряжений.
Найдём формулы для вычисления относительного угла закручивания и касательных напряжений. Силы в сечении, порождаемые касательными напря- жениями, в сумме дают внутренний крутящий момент в сечении:
i=∞ |
i=∞ |
Fi = òτxαrdF . |
|
||
M x (x)= å |
(τxαi |
Fi )ri = å |
τxαiri |
(14.5) |
|
i=1 |
|
i=1 |
|
F |
|
Здесь, как и раньше в подобных случаях, бесконечная сумма заменена интегра- лом. Значение момента M x (x) в сечении можно определить построением эпюр.
Подставим в полученное равенство выражение для касательного напря- жения. Учитывая постоянство величин G и ξ по сечению, получим
M x (x)= òGξr 2 dF = Gξò r 2 dF . |
(14.6) |
|
F |
F |
|
Входящий в формулу интеграл является по определению полярным моментом инерции, поэтому
M x (x)= GI pξ = GI p |
dϕ |
. |
(14.7) |
|
|||
|
dx |
|
|
Это соотношение упругости, которое связывает внутренний момент в сечении с компонентами перемещений, в данном случае с углом поворота сечений. Из
- 159 -
соотношения упругости можно вычислить относительный угол закручивания:
ξ = |
M x (x) |
. |
(14.8) |
GI p |
Подставив ξ в (14.3), получим формулу для вычисления касательных на- пряжений при кручении круглого стержня:
τxα = |
M x (x) |
r . |
(14.9) |
||
I p |
|
||||
|
|
|
|||
Из формулы видно, что, как и в других случаях деформирования стержня, на- пряжения в нём не зависят от свойств его материала. Полученное касательное
|
|
y |
|
τxz |
|
r |
|
|
α |
||
τxα |
α |
||
τxy |
|||
z |
|
0 |
|
|
Рис. 14.10 |
||
напряжение изменяется по координате x как момент, зависимость от r уже рас- смотрена, так что в общем случае τxα – функция двух переменных τxα = τxα (x,r).
Однако |
в |
задаче |
на |
рис. 14.1 |
M x (x)= M x = const и |
τxα = τxα (r), т.е. |
|||
касательные |
напряжения по |
длине |
||
стержня не менялись.
Напряжения найдены в цилиндри- ческой системе координат. По ним не-
сложно найти напряжения в привычной декартовой системе координат. Как
видно из рис. 14.10: |
|
M x (x) |
|
||||
τxy = −τxα sin α = −Gξr sin α = −Gξz = − |
z , |
||||||
|
I p |
|
|||||
|
|
|
(14.10) |
||||
τxz = τxα cosα = Gξr cosα = Gξ y = |
M x (x) |
|
|
||||
y . |
|
||||||
I p |
|
|
|
||||
|
|
|
|
|
|
||
Напомним, что при кручении справедливо уравнение равновесия, которое решается (интегрируется) в процессе построения эпюры крутящих моментов
dM x (x) |
+ mx = 0 . |
(14.11) |
||
dx |
|
|||
|
|
|||
Перемещения при кручении
Перемещения точек при кручении круглого стержня полностью опреде- ляются, как нетрудно видеть, углами поворота поперечных сечений ϕ(x). Дей-
ствительно, эти углы определят положение жестких дисков поперечных сече- ний, а следовательно, и всех точек внутри этих дисков. Углы ϕ(x) можно найти
интегрированием соотношения упругости при кручении (14.7):
- 160 -
x dϕ(x) |
x |
M |
x |
(x) |
|
||||
ò |
|
dx = ò |
|
|
|
|
dx , |
||
dx |
GI |
p |
|||||||
xн |
xн |
|
|||||||
|
|
|
|
|
|||||
откуда
ϕ(x)− ϕ(xн )= òx M x (x)dx ,
xн GI p
или
ϕ(x)= ϕ(xн )+ |
x |
M x (x) |
dx . |
|
||
ò |
|
|
|
(14.12) |
||
GI |
p |
|||||
|
xн |
|
|
|
||
Итак, получена общая формула для вычисления углов поворота сечений при кручении стержней. В большом числе практически важных задач распреде- ленный крутящий момент отсутствует ( mx = 0 ), тогда из уравнения равновесия (14.11) следует, что M x (x)= const . Если жесткость на кручение тоже постоян- на, то эти величины выйдут из-под знака интеграла и углы поворота сечений
выразятся соотношением
ϕ(x)= ϕ(xн )+ |
M x (x)(x − xн ) . |
|
|
(14.13) |
|||
|
|
GI p |
|
|
|
|
|
y |
|
M x |
В |
случае, |
изображенном |
на |
|
|
рис. 14.1 и 14.11, |
в сечении заделки |
|||||
|
|
|
|||||
|
|
x |
xн = 0, |
угол поворота в этом сечении |
|||
Эпюра M x (x) |
M x |
также равен нулю: ϕ(xн )= 0 ; внутренний |
|||||
момент |
M x (x) в любом сечении равен |
||||||
|
|
||||||
|
|
|
внешнему моменту M x , приложенному к |
||||
|
Рис. 14.11 |
концу стержня. Поэтому предыдущее со- |
|||||
|
отношение примет вид: |
|
|||||
|
M x x , |
|
|
||||
ϕ(x)= |
|
|
|
(14.14) |
|||
|
GI p |
|
|
|
|
|
|
угол поворота свободного конца стержня запишется:
ϕк = ϕ(x = l)= M xl .
GI p
Последнее соотношение можно переписать и так:
M x = GI p ϕк 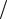 l .
l .
(14.15)
(14.16)
Соотношения (14.15), (14.16) связывают приложенный внешний момент с углом поворота того же сечения для стержня на рис. 14.11. Заметим, что соотношение (14.16) является частным случаем соотношения (14.7) для задачи на рис. 14.11.
