
Lectures part1
.pdf- 131 -
стант шесть C1, D1, C2 , D2 , C3 , D3 . Для их определения снова можно записать
условия опирания балки, которые дают два уравнения для определения кон- стант:
v(x = l2 )= 0, v(x = l3 )= 0 . |
(12.27) |
Очевидно, что этих уравнений недостаточно. Нужно найти ещё четыре условия, чтобы задача определения констант интегрирования стала разрешимой. Такими условиями являются условия стыковки участков (их ещё можно назвать усло- виями неразрывности деформаций или перемещений). Балка рассматривается до разрушения, поэтому можно утверждать, что на границах участков функции прогиба балки v(x) и угла поворота поперечных сечений θ(x) должны быть не- прерывны. Иными словами, прогибы балки слева и справа от точки стыка, как и углы поворота поперечных сечений, должны быть равны. Так что для стыка в
точке x = l1 : |
|
vI (x = l1 )= vII (x = l1 ) , |
(12.28) |
θI (x = l1 )= θII (x = l1 ) , |
(12.29) |
для стыка в точке x = l2 : |
|
vII (x = l2 )= vIII (x = l2 ) , |
(12.30) |
θII (x = l2 )= θIII (x = l2 ) , |
(12.31) |
где римскими цифрами отмечены номера участков.
Теперь количество констант и уравнений для их определения совпадают, и константы могут быть найдены из полученной системы линейных алгебраи- ческих уравнений. Однако если вести расчет вручную, решение системы шести уравнений с шестью неизвестными будет весьма трудоёмкой задачей.
Задача будет разрешимой и для балки с произвольным числом участков. Действительно, стыков будет на единицу меньше числа участков, тогда усло- вий стыковки участков будет на два меньше числа неизвестных констант. Не-
достающие два условия всегда можно получить из условий закрепления всей балки.
Когда определены константы, формулы углов поворота сечений и проги- бов становятся вычисляемыми выражениями и задачу определения перемеще- ний в балке можно считать решенной.
Метод уравнивания произвольных постоянных интегрирования (метод начальных параметров, метод Клёбша)
Число констант при интегрировании уравнения изогнутой оси можно све- сти всего к двум, если специальным образом записывать соответствующие со- отношения. Тогда для определения констант придется решать систему уравне-
- 132 -
ний максимально всего двух уравнений. Соответствующие приёмы (правила записи соотношений) проще ввести, а затем показать на примере, почему они приводят к результату.
Соотношения следует записывать так, чтобы все слагаемые предыдущих участков без изменения входили бы в выражения для последующих участков, а
дополнительные слагаемые последующих участков обращались бы в нуль на границе с предыдущим участком. Такая структура соотношений получится, ес- ли выполнить следующие правила (правила Клёбша):
1.Отсчет абсцисс всех участков должен вестись от одного начала коорди- нат – крайней левой (или правой) точки оси балки, т.е. для всей балки вводится единая глобальная система координат.
2.При записи уравнений равновесия всегда должна использоваться часть балки с началом координат.
3.Выражение изгибающего момента от сосредоточенной пары M следу-
ет записать в виде M (x − a)0 , где a - абсцисса сечения, в котором приложен момент M .
4.Если при последовательном рассмотрении участков балки в порядке, соответствующем возрастанию координаты x , обнаруживается, что появляю- щаяся на каком-либо участке распределенная нагрузка не продолжается на по- следующих участках, то ее следует искусственно продолжить до конца балки, а
для исключения действия добавленной нагрузки приложить нагрузку той же интенсивности, но противоположного направления.
5.Интегрирование дифференциального уравнения изогнутой оси балки должно вестись без раскрытия скобок.
Когда выражения для моментов, углов поворота и прогибов получены, следует проконтролировать получение требуемой структуры соотношений.
|
P =15 кН |
M* = 50 кНм |
|
q = 30 кH/м |
A |
B |
q = 30 кH/м |
|
|||
|
l1= 2м |
l2= 4м |
l3= 3м |
|
|
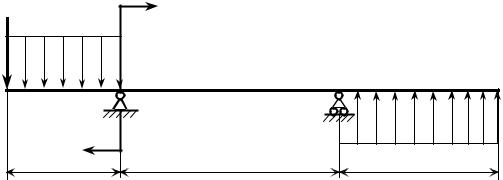
Рис. 12.3 |
|
- 133 -
Рассмотрим пример на рис. 12.3. Введем для рассматриваемой балки еди- ную глобальную декартову систему координат 0xyz следующим образом. Со- вместим начало координат − точку 0 с левым торцом балки (рис. 3.5). Ось 0x совместим с осью балки, а ось 0y направим вертикально вверх. Тогда ось 0z, дополняющая координатную систему до правой системы координат, своим ост- рием будет направлена на читателя (рис. 12.4).
Применим обычный алгоритм построения эпюр. Первый пункт алгоритма (определение опорных реакций) выполняется обычным способом. В данной за-
даче
RA =118,75 кН, |
RB = −133,75 кН . |
|
|
|
|||
|
y |
q |
RA |
M* |
RB |
|
|
P |
|
|
|
|
|||
|
|
|
|
|
|
|
|
0 |
|
|
|
A |
B |
|
С |
|
|
x |
X1 |
X2 |
|
X3 |
q |
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
q |
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
a1 = 2 м |
|
|
|
|
|
|
|
|
|
a2 = 6 м |
|
|
|
|
|
|
|
a3 = 9 м |
|
|
|
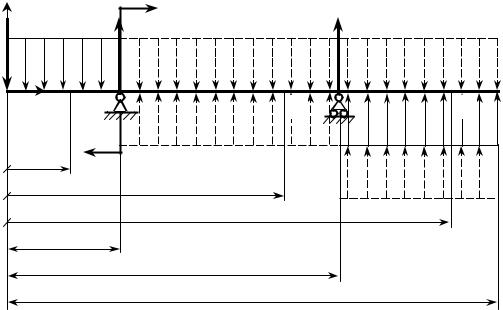
Рис. 12.4
При выполнении второго пункта (разбиении балки на участки) следует искусственно продолжить распределенную нагрузку, как показано на рис. 12.4. Кроме того, лучше заменить все продольные размеры балки размерами, изме- ренными от начала координат.
В третьем пункте алгоритма (при записи уравнений равновесия отсечён- ной части) следует рассматривать равновесие части балки с началом координат. Сосредоточенный момент следует умножить на множитель (x − a)0 . Получен- ные выражения изгибающего момента следует дважды проинтегрировать, не раскрывая скобок. Константы интегрирования будем пока считать разными на разных участках и докажем их равенство.
Участок 1 [0А]: 0 ≤ x1 ≤ a1 . Запишем уравнения равновесия отсечённой части:
- 134 -
åPy i = 0 = -P - q × x1 - Qy (x) ,
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
åM X1 j = 0 = Px1 + q |
|
|
+ M z (x). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
Отсюда находим аналитические выражения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Qy (x)= −P − qx1 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
(x)= EI |
|
|
d |
2v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
M |
z |
|
z |
|
|
|
1 |
|
|
= -Px - q |
1 |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
dx2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
1 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
q (x)= C - P × |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
EI |
|
1 |
|
|
|
- q |
1 |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
z |
|
1 |
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
v (x)= D + C x - P |
x3 |
|
|
|
|
|
|
|
x |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
EI |
|
|
|
|
1 |
|
- q |
|
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
z |
|
1 |
|
|
|
|
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
Участок 2 [АB]: a1 ≤ x2 ≤ a2 . Уравнения равновесия: |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
åPy i = 0 = −P − qa1 + RA − Qy (x) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− a )2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
å |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x |
2 |
|
|
|
|
|
|
(x |
|
|
|
− a )0 + M |
|
(x) . |
||||||||||||||||||||||
M |
|
|
= 0 = Px |
|
+ q |
|
|
|
2 |
− R |
|
|
|
(x |
|
|
|
− a ) − q |
|
|
|
|
|
|
1 |
|
|
|
− M |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
X |
2 j |
2 |
|
|
|
|
|
A |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
z |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||||||||||
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
Аналитические выражения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
Qy (x)= -P - q × a1 + RA , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
(x)= EI |
|
|
d 2v(x) |
= −Px |
|
|
|
|
− q |
|
x2 |
|
+ R |
|
|
|
|
|
|
− a ) + q |
(x |
2 |
− a )2 |
+ M (x |
|
− a )0 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
M |
z |
z |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
A |
(x |
|
|
|
|
|
|
|
1 |
|
|
|
|
, |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
dx2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
||||||||||||||
|
|
|
|
|
|
(x)= C |
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
(x |
2 |
- a )2 |
|
|
|
(x |
2 |
|
- a )3 |
+ M (x |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
EI |
z |
q |
2 |
2 |
+ P |
2 |
|
|
|
- q |
|
|
2 |
|
|
+ R |
A |
|
|
|
|
|
|
|
1 |
|
|
|
+ q |
|
|
|
|
|
|
1 |
|
|
|
2 |
- a ) , |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
EI z v2 (x) = D2 - C2 x2 - P × |
|
x3 |
|
|
|
|
|
|
x |
4 |
|
|
|
|
|
|
|
(x |
2 |
- a )3 |
|
|
|
|
|
(x |
2 |
- a )4 |
|
(x |
2 |
- a )2 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
- q |
|
2 |
|
|
+ RA |
|
|
|
|
|
1 |
|
|
+ q |
|
|
|
1 |
|
+ M |
|
|
|
1 |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
6 |
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
|
|
|
|
|
2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
Участок 3 [BC]: a2 ≤ x2 ≤ a3 . Уравнения равновесия: |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
åPy i = 0 = -P - qa1 + RA + RB + q(x3 - a2 )- Qy (x) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- a )2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
åM X 3 j = 0 = Px3 + q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x |
3 |
- M (x3 - a1)0 - |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
3 |
|
|
|
- RA (x3 - a1) - q |
|
|
|
|
|
|
1 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
- q |
(x3 - a2 )2 |
|
- RB (x3 - a2 )+ M z (x)= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Аналитические выражения:
Qy (x)= −P − qa1 + RA − RB + q(x3 − a2 ) ,

- 135 -
|
|
|
(x) = EI |
|
d |
2v |
3 |
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x |
3 |
- a )2 |
|
|
|
|
|
|
|
|
|
||||||||||||
M |
|
|
|
|
|
|
|
= -Px |
|
- q |
3 |
|
|
+ R |
|
|
(x |
|
- a ) + q |
|
|
|
|
1 |
|
|
+ M (x |
|
- a )0 |
+ |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
z |
|
|
|
|
z dx2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
3 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ q |
(x3 − a2 )2 |
|
|
+ R |
B |
(x − a |
2 |
) |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
(x)= C |
|
|
|
|
|
|
x2 |
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
(x − a ) |
2 |
|
|
|
|
|
(x |
3 |
− a )3 |
+ M (x |
|
|
|
|
||||||||||||||||||||||||
EI |
z |
θ |
3 |
3 |
− P |
|
|
3 |
− q |
|
3 |
+ |
R |
A |
|
|
|
|
3 |
|
|
|
|
|
1 |
|
+ q |
|
|
|
|
1 |
|
|
|
3 |
− a ) + |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
1 |
|
|
||||||||||
|
|
|
|
|
|
|
+ q |
(x3 − a2 )3 |
|
|
+ RB |
|
|
(x3 − a2 )2 |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
v (x)= D + C |
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
x4 |
|
|
|
|
|
|
|
(x − a )3 |
|
|
(x |
3 |
− a )4 |
+ M |
(x − a )2 |
|||||||||||||||||||||||||||||||
EI |
|
|
x − P |
3 |
− q |
|
|
|
3 |
+ R |
A |
|
|
3 |
|
|
|
1 |
|
|
+ q |
|
|
|
1 |
|
3 1 |
+ |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
z |
3 |
|
3 |
|
|
|
|
3 |
3 |
|
|
|
|
|
6 |
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
24 |
|
|
|
|
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
+ q |
(x3 − a2 )4 |
+ RB |
(x3 − a2 )4 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
Можно видеть, что желаемая структура соотношений получена. Заметим, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
что скобка (x − a)0 даёт при x = a |
|
неопределенность вида 00 . К противоречиям |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
это не ведет, если доопределить в этой задаче данное выражение так: 00 = 0 .
Условие стыковки первого и второго участков по углу поворота сечений
имеет вид:
EIzθ1(x = a1)= EIzθ2 (x = a1) .
Подстановка сюда соотношений для углов поворота приводит к равенству
|
a2 |
|
a3 |
|
|
a2 |
a3 |
|
|
(a − a )2 |
||
C − P |
1 |
− q |
1 |
= C |
2 |
− P |
2 |
− q |
2 |
+ R |
A |
1 1 |
|
|
|
|
|
||||||||
1 |
2 |
|
6 |
|
|
2 |
|
6 |
|
2 |
||
|
|
|
|
|
|
|
|
|||||
из которого следует, что C1 = C2 = C .
Условие стыковки участков по прогибам
EIzv1(x = a1 )= EI zv2 (x = a1 )
приводит к равенству
+ q (a1 − a1)3 + M (a1 − a1) , 6
|
a3 |
|
|
a4 |
|
|
a3 |
|
a4 |
|
×0 + q ×0 + M ×0 , |
|||
D + Ca - P |
1 |
|
- q |
1 |
= |
D - Ca - P |
1 |
- q |
1 |
+ R |
A |
|||
|
|
|
|
|
||||||||||
1 |
1 |
6 |
24 |
|
2 |
1 |
6 |
24 |
|
|
||||
из которого следует D1 = D2 = D . |
|
|
|
|
|
|
||||||||
|
Точно так же записываются условия стыковки второго и третьего участка: |
|||||||||||||
|
EIzθ2 (x = a2 )= EI zθ3 (x = a2 ) , |
|
|
|
|
|
||||||||
|
EIzv2 (x = a2 )= EI zv3 (x = a2 ) , |
|
|
|
|
|
||||||||
откуда следует, что C2 = C3 = C , D2 = D3 = D . |
|
|||||||||||||
|
Таким образом, |
C1 = C2 = C3 = C , D1 = D2 = D3 = D , что и требовалось |
||||||||||||
доказать. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Видно, |
что равенство констант обеспечивается специальной структурой |
||||||||||||
выражений для углов поворота сечений и прогибов, когда все слагаемые пре-
- 136 -
дыдущих участков без изменения входят в выражения для последующих участ- ков, а дополнительные слагаемые последующих участков обращаются в нуль на границе с предыдущим участком.
В результате в выражениях для углов поворота сечений и прогибов со- держится всего две константы, которые необходимо найти из условий опирания всей балки, в данном случае из условий равенства нулю прогибов балки на опо-
рах (рис. 12.4)
v1(x = a1 )= 0 , v2 (x = a2 )= 0 .
Подстановка в эти условия функций EIzv1(x) и EIzv2 (x) при x = a1 и x = a2 со-
ответственно приводит к уравнениям:
ìD + Ca - P |
a13 |
|
- q |
a14 |
|
= 0 , |
|
|
|
||||
|
|
|
|
|
|
||||||||
ï |
1 |
|
6 |
|
|
24 |
|
|
|
|
|
||
ï |
|
|
|
|
|
|
|
|
|
||||
í |
|
|
|
a3 |
|
|
a4 |
|
(a |
|
- a )3 |
||
ï |
|
|
|
|
|
|
2 |
||||||
|
|
2 |
|
|
2 |
|
|
|
1 |
||||
ïD + Ca2 |
- P |
|
|
|
- q |
|
|
|
+ RA |
|
|
|
|
6 |
|
24 |
|
|
6 |
||||||||
î |
|
|
|
|
|
|
|
||||||
|
(a |
2 |
- a )4 |
+ M |
(a |
2 |
- a )2 |
|
+ q |
|
1 |
|
1 |
, |
|||
|
|
24 |
|
|
2 |
|||
|
|
|
|
|
|
|
которые образуют систему двух уравнений с двумя неизвестными относительно констант интегрирования C и D. Подстановка исходных данных приводит к
системе
ìD + 2C = 40 , íîD + 6C =173,44 ,
откуда находим С = 33,36 кН × м2 , D = -26,72 кН × м3 . После определения кон-
стант полученные соотношения становятся вычисляемыми и можно построить эпюры величин θ(x)и v(x) для данной задачи. Более подробно данный пример
рассмотрен в пособии по выполнению расчетно-графических работ.
Заметим, что слагаемые соотношений для основных величин задачи Qy (x), M z (x), θ(x), v(x) записываются по определенным законам, а из соотно-
шений для последнего участка отбрасыванием слагаемых получаются соотно- шения для всех других участков. Очевидно, что если положить, что скобка (x − ai )≡ 0 при x ≤ ai , то несложно записать общее выражение для любой из
этих величин. Например, так запишется общий вид уравнения изогнутой оси балки (функции прогибов):
EIzv(x)= EIzv0 - EIzq0x2 + åMi |
(x - a )2 |
+ åPj |
(x - a j )3 |
+ åqk |
(x - a )4 |
|
|
i |
|
k |
, (12.32) |
||||
2 |
6 |
24 |
|||||
i |
j |
k |
|
где учтены формулы (12.23) и (12.24) для констант интегрирования. Формулой (12.32) и ей подобными возможно не слишком удобно пользо-
ваться при ручном счёте, зато они весьма полезны при программировании.

|
|
|
|
- 137 - |
|
|
|
|
Проверка прочности и жесткости при изгибе. Подбор поперечных |
||||
|
|
сечений |
|
|
|
|
M z (x) |
|
y |
Эп. σx (y) Эп. τxy (y) |
Рассмотрим |
напряженное |
со- |
|
|
стояние в балке, подвергающейся попе- |
||||
|
|
|
|
речному изгибу. Для прямоугольного |
||
h |
|
|
|
поперечного сечения законы распреде- |
||
|
|
|
ления нормальных |
и касательных |
на- |
|
z |
|
Qy (x) |
||||
|
пряжений, а также и внутренние сило- |
|||||
|
|
|||||
|
|
|
|
вые факторы, связанные с этими на- |
||
|
|
|
σx max τxy max |
пряжениями показаны на рис. 12.5. |
|
|
|
b |
|
Вблизи верхней и нижней по- |
|||
|
|
|
Рис. 12.5 |
верхности балки действуют максималь- |
||
|
|
|
ные в сечении (по модулю) нормальные |
|||
|
|
|
|
|||
напряжения, а касательные в этой зоне – нулевые или близкие к нулю. Других |
||||||
напряжений в материале нет, если принять гипотезу ненадавливания продоль- |
||||||
ных волокон. Поэтому напряженное состояние здесь близко к одноосному. |
||||||
Вблизи нейтральной линии, напротив, нормальные напряжения нулевые или |
||||||
близки к нулю, зато действуют максимальные (по модулю) касательные напря- |
||||||
жения. Такое напряженное состояние, по определению, близко к чистому сдви- |
||||||
гу в материале. В других зонах сечения действуют нормальные напряжения σx , |
||||||
зависящее от изгибающего момента, и на тех же площадках действует каса- |
||||||
тельное напряжение τxy , зависящее от перерезывающей силы. Других напря- |
||||||
жений, в том числе σy , в материале нет или они малы. Поскольку нормальное и |
||||||
касательное напряжения напрямую не связаны, то это разновидность плоского |
||||||
напряженного состояния в плоскости x0y. |
|
|
||||
В зоне одноосного напряженного состояния прочность можно проверять |
||||||
как при осевом растяжении-сжатии. Если считать, что материал одинаково со- |
||||||
противляется растяжению и сжатию, то условие прочности запишется так: |
|
|||||
σx max ≤ [σ]раст . |
|
(12.33) |
||||
Случай разных ограничений на растяжение и сжатие достаточно часто встреча- |
||||||
ется в расчетах, но здесь не рассматривается. |
|
|
||||
В зоне чистого сдвига прочность принято проверять по касательным на- |
||||||
пряжениям. Условие прочности для них записывается так же, как для нормаль- |
||||||
ных напряжений: |
|
|
|
|||
τxy |
max |
≤ [τ]сдвиг . |
|
(12.34) |
||
|
|
|
|
|
||
Назначение допускаемых касательных напряжений может производиться |
||||||

- 138 -
примерно по той же методике, что и для нормальных напряжений. Но возмож- но их назначение и как доли от допускаемых касательных напряжений. Напри- мер, при осевом растяжении-сжатии ограничение максимальных нормальных напряжений означает ограничение и максимальных касательных напряжений, поскольку в этом случае τ max = 0,5σ max . Если считать, что при разных напря-
женных состояниях должны быть одинаковые ограничения по напряжениям,
тогда следует принять
[τ]сдвиг = 0,5[σ]раст . |
(12.35) |
Для стальных балок обычно принимают |
|
[τ]сдвиг = (0,5...0,6)[σ]раст , |
(12.36) |
Для хрупких материалов коэффициент увеличивают, для анизотропных мате- риалов, плохо сопротивляющихся сдвигу, его уменьшают.
В зоне плоского напряженного состояния напряжения не достигают мак- симальных значений, поэтому обычно считают, что в данном случае разруше- ния не должно происходить, и ограничиваются проверками прочности по мак- симальным нормальным и касательным напряжениям. Практика показывает, что обычно это оправданно.
Условие прочности в сечении (12.33) с учетом формулы для нормальных
напряжений при изгибе приводит к соотношению
|
σx |
|
max |
= |
|
M z (x) |
|
|
≤ [σ]раст |
, |
(12.37) |
||||
|
|
|
|
||||||||||||
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Iz |
|
y |
|
max |
|||||||||
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||
где обозначают
Wz = yIz . (12.38)
max
В результате условие прочности по нормальным напряжениям для всей балки принимает вид:
|
σ |
x |
|
|
= |
|
|
M z (x) |
|
max |
≤ [σ] |
, |
(12.39) |
|
|
|
|
|
|
||||||||
|
|
|
|||||||||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
max |
|
|
|
|
|
|
раст |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
Wz |
|
|
|||
где учтено, что максимальное нормальное напряжение во всей балке возникнет в сечении с наибольшим изгибающим моментом. Величину Wz называют осе-
вым моментом сопротивления сечения.
Проверку прочности балки (решение прямой задачи) начинают с проверки выполнения данного условия. Если оно выполняется, то дополнительно проверя- ют условие прочности по касательным напряжениям. Для прямоугольных и мно- гих других сечений, особенно если балка с малой относительной толщиной, каса- тельные напряжения много меньше нормальных. Тогда проверка по касательным напряжениям не обязательна, но для двутаврового сечения, а также материалов,

- 139 -
слабо сопротивляющихся сдвигу, и в некоторых других случаях она необходима.
Касательное напряжение может быть грубо определено как среднее по сечению. Тогда условие прочности по касательным напряжениям принимает
вид
t |
xy |
|
|
= |
|
Qy (x) |
|
max |
£ [t] |
. |
(12.40) |
|
|
|
|
||||||||
|
|
||||||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
||||||
|
|
max |
|
|
F |
|
сдвиг |
|
|
||
|
|
|
|
|
|
|
|||||
Однако погрешность вычислений по этой формуле слишком высока, поэтому предпочтительно пользоваться формулой Журавского, что приводит к следую- щему условию прочности:
|
|
|
|
|
Qy (x) |
|
æ |
~ |
ö |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||||
txy |
|
|
= |
|
|
|
max ç |
Sz (y) |
÷ |
£ [t]сдвиг . |
(12.41) |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
ç |
b(y) |
÷ |
||||
|
max |
|
Iz |
|
||||||||
|
|
|
|
|
||||||||
|
|
|
|
|
è |
ømax |
|
|
||||
Максимум геометрической характеристики в круглых скобках для симметрич- ных по высоте сечений достигается на оси симметрии (нейтральной линии) се- чения; тогда условие прочности по касательным напряжениям запишется так:
|
|
|
|
|
|
Qy (x) |
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
txy |
|
|
= |
|
|
max |
Sz max |
£ [t]сдвиг , |
(12.42) |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|||||
|
|
max |
|
Izb0 |
|
||||||
|
|
|
|
|
|
|
|
||||
~ |
|
~ |
|
|
= b(y = 0) . |
|
|||||
|
|
|
|
|
|
|
|||||
где Sz max = Sz (y = 0), b0 |
|
||||||||||
Балку обычно считают прочной, если выполняются условия прочности по нормальным и касательным напряжениям (12.39) и (12.42). Однако могут по- требоваться и дополнительные проверки прочности: по касательным напряже- ниям τxz (формула (11.29)), напряжениям надавливания продольных волокон σy , а также проверки прочности, учитывающие сложный характер напряжен-
ного состояния.
Поперечное сечение выбирается (обратная задача) по максимальному нормальному напряжению σx во всей балке. Условие для подбора сечения по-
лучается из неравенства (12.39)
Wz ³ |
|
M z (x) |
|
max |
. |
(12.43) |
|
|
|||||
|
|
|
||||
|
|
|
|
|||
|
|
[s]раст |
|
|||
Однако из одного условия можно подобрать только один параметр поперечного сечения. Если балка выполнена из стандартного прокатного профиля, необхо- димый номер профиля можно определить из этого неравенства по ряду значе- ний Wz в таблице стандартных профилей. Следует выбирать профиль ближай- ший, превосходящий требуемую величину по значению Wz , чтобы не перетя-
желять балку.
Для прямоугольного сечения

|
|
|
|
|
|
|
|
|
|
= bh3 12 = bh2 |
|
- 140 - |
||||
W = |
|
|
|
Iz |
, |
(12.44) |
||||||||||
|
|
|
|
|||||||||||||
|
z |
|
|
|
y |
|
|
|
|
h 2 |
6 |
|
|
|||
|
|
|
|
|
|
max |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
поэтому условие (12.43) примет вид |
|
|||||||||||||||
|
bh |
2 |
³ |
|
|
M z (x) |
|
max |
, |
|
|
(12.45) |
||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
6 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
[s]раст |
|
|
|
||||||
откуда видно, что невозможно подобрать прямоугольное сечение только из это- го условия, поскольку геометрия прямоугольного сечения, в том числе момент сопротивления, определяется двумя параметрами (b и h), а используется только одно неравенство.
Условие прочности по касательным напряжениям (12.42) для подбора се- чений не принято использовать, поскольку поперечный размер сечения, полу- ченный с его использованием, оказывается обычно слишком малым, неприем- лемым по другим причинам. Один из размеров может быть выбран из иных со- ображений: например, ширина сечения может быть обусловлена толщиной лис- та заготовки, а высоту можно подобрать с помощью условия (12.45). В других случаях может быть задано соотношение между b и h: h = kb . Тогда из (12.45) снова можно найти размеры сечения:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b = 3 |
6 |
|
M z (x) |
|
max |
|
, h = kb . |
(12.46) |
|||||
|
|
|
|||||||||||
|
|
|
|
|
|||||||||
|
k2[s] |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
раст |
|
|
|
|
|
|
|
||
При подборе полых сечений, например трубы, момент сопротивления вы- |
|||||||||||||
числяется по формуле |
|
|
|
|
|
|
|
||||||
Wz = (I z сплошное - I z отверстие ) |
|
y |
|
max , |
(12.47) |
||||||||
|
|
||||||||||||
|
|
|
|||||||||||
поскольку моменты инерции относительно одной и той же оси можно склады- вать, т.е. они обладают свойством аддитивности. Следует иметь в виду, что мо- мент сопротивления этим свойством не обладает, поскольку это не просто ин- теграл, а более сложная величина. Действительно
Wz сплошное -Wz отверстие = |
|
|
Iz сплошное |
- |
|
|
Iz отверстие |
¹ Wz . |
(12.48) |
||||
|
|
y |
|
max сплошное |
|
|
y |
|
max отверстие |
||||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||
Если необходимо, полученное сечение проверяют по касательным напря- жениям. Изредка это условие может не выполняться. Тогда сечение усиливают, например, выбирают следующий по номеру профиль. Обычно ближайший про- филь удовлетворяет данному условию. Если же нет, то операцию повторяют до тех пор, пока оно не выполнится.
При проверке жесткости выясняется, не выходят ли параметры деформи- рованного состояния балки за пределы допускаемых значений. В отличие от ограничений по прочности ограничения по жесткости могут быть весьма раз-
