Lectures part1

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский национальный исследовательский технический университет им. А. Н. Туполева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

вать уравнение изогнутой оси балки

= M z (x),

.pdf

Скачиваний:

Добавлен:

12.03.2015

Размер:

1.35 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1813 14 15 16 17 18 > Следующая >>>

- 121 -

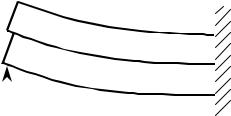
будем считать, что сечение балки несимметрично относительно оси z. Тогда нейтральный слой и плоскость x0z проходят не в середине высоты её сечения. На рис. 11.5 изображен этот элемент, его поперечное сечение, а также. нор- мальные напряжения, действующие от отброшенных левой и правой частей стержня (показаны истинные направления их действия в задаче на рис. 11.1), значения которых вычисляются по формулам чистого изгиба:

sx (x, y)= - MIzz(x()+y), (11.6) sx (x+ , y)= - M zIzx y .

На некотором уровне y проведем ещё одно, горизонтальное сечение CDD3C3 (параллельно плоскости x0z) и рассмотрим равновесие части элемента

балки выше рассматриваемого уровня (рис. 11.6).

Вычислим силы N(x, y) и N (x+ , y), вызванные нормальными напряже- ниями от изгиба σx (x, y) и sx (x+ , y) (рис. 11.5). Обозначим площадь отсечен-

ной части сечения:
FDD		~	(11.7)
	D D = F
3	2	1

Если сечение не меняется по длине стержня, то такая же площадь и у части се- чения CC3C2C1. Поскольку определенный интеграл представляет собой беско-

нечную сумму, получим с учетом (11.6)

M z (x)

N(x, y)= òsx (x, y)dF

= -

y÷dF

(x+ )

N(x

, y)= òsx (x

, y)dF

y÷dF

	M z (x)			~
			ò ydF ,
			ò ydF ,
	Iz F
			~
		M z (x+ )				~
= -					ò ydF .
= -		Iz			ò ydF .
		Iz			F
					~

(11.8)

(11.9)

Интеграл, входящий в эти формулы, представляют собой по определению ста-

тический момент площади F относительно оси z. Обозначим статический мо- мент отсечённой части сечения DD3D2 D1:

	отс	~			ò~ ydF ,
S		= Sz (y)=			ò~ ydF ,				(11.10)
				F
тогда осевые силы (11.8) , (11.9) запишутся так:
			M z		(x) ~
N(x, y)= -							Sz (y) ,		(11.11),
N(x, y)= -				Iz			Sz (y) ,		(11.11),
N(x+ , y)= -				Iz		(x+ )~
				M	z	(x+ )~
					z			Sz (y).	(11.12)
								Sz (y).	(11.12)
					Iz

На рис. 11.6 изображены истинные направления этих сил в задаче на рис. 11.1.

- 122 -

Входящие в соотношения (11.11) , (11.12) моменты M z (x) и M z (x+ ) при поперечном изгибе не равны. Следовательно, не равны и силы N(x, y) и N (x+ , y). Уравновесить разницу этих сил могут только касательные напряжения

на нижней площадке, связывающей рассматриваемую часть с остальным мате- риалом элемента балки. Эти касательные напряжения τ yx также изображаем на

рис. 11.6 действующими в их истинном направлении. Считаем, что они равно- мерно распределены по площадке CDD3C3 .

Запишем условие равновесия отсеченной части в направлении оси x:

å Xi = 0 = N(x, y)− N(x+ , y)+ τyxb(y)dx .			(11.13)
	i
Подстановка сюда (11.11), (11.12) дает
	M z (x+ )− M z (x) ~
		Sz (y)+ τyxb(y)dx = 0.	(11.14)

	Iz
В непрерывной дифференцируемой задаче значения функций в бесконеч-
но близких точках также бесконечно близки, поэтому
	M z (x+ )= M z (x)+ dM z (x).		(11.15)

Тогда, рассматривая равенство τyx , получаем

		~
τyx = −	dM z (x) Sz (y)			.

	dx		Izb(y)

(11.14) как уравнение, из которого можно найти

(11.16)

Учитывая закон парности касательных напряжений и уравнение равнове- сия (11.1), приходим к формуле, которую называют формулой Журавского:

~
τxy (x, y)= τyx (y, x)= −	Qy (x)Sz (y)	.	(11.17)

	Izb(y)

Для задач в плоскости x0y , если не указывать индексы и функциональные за- висимости, формулу можно записать проще:

~
	τ = −	Q S	.	(11.18)
	τ = −		.	(11.18)
		I b
				(Для облегчения запоминания её называ-
				ют формулой «турксиб», в этом слове
				звучат все буквы, составляющие форму-
				лу).
P				Касательные напряжения в попе-
				речном сечении τxy нами найдены с по-
				речном сечении τxy нами найдены с по-
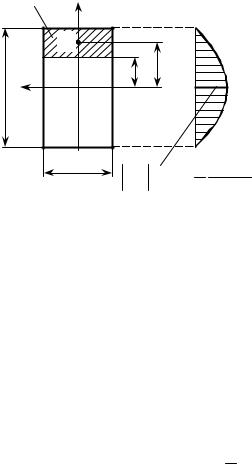
		Рис. 11.7		мощью парных им напряжений τyx . По-

- 123 -

ясним появление последних напряжений при поперечном изгибе. Если балка состоит из двух частей, как показано на рис. 11.7, то её торцевое сечение обра- зует уступ, и соприкасающиеся поверхности частей балки проскользнут друг по другу. В сплошной балке этим скольженьям препятствовали касательные на- пряжения τ yx . При чистом изгибе такие напряжения не возникают.

	Как и нормальны, касательные напряжения не зависят от свойств мате-
риала. При прочих равных условиях напряжения в резиновой и стальной балке
при малых перемещениях и деформациях одинаковы.
	Полученная формула Журавского не слишком проста и наглядна. Можно
~					видеть, что касательные напряжения, вы-
~					численные по этой формуле, принимают
F (y)		y	Эпюра txy (y)		численные по этой формуле, принимают
F (y)		y	Эпюра txy (y)		нулевые значения вблизи верхней и ниж-
		C			нулевые значения вблизи верхней и ниж-
		C			ней кромок сечения. Действительно, ста-
			c		ней кромок сечения. Действительно, ста-
h			y y		тические моменты нулевой площади на
					тические моменты нулевой площади на
	z				верхней кромке и статический момент
	z				верхней кромке и статический момент
					всего сечения относительно его цен-
		b	3 Qy (x)		тральной оси у нижней кромки равны
		b	3 Qy (x)		нулю, что и обнуляет напряжения. Но
			txy max = 2	F	закон изменения касательных напряже-
		Рис. 11.8			ний по высоте сечения не очевиден.
		Касательные напряжения в балке прямоугольного сечения при по-
		перечном изгибе

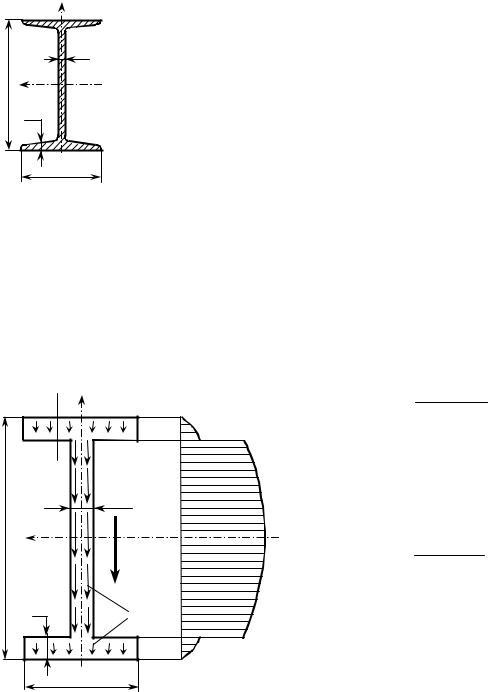
Получим закон изменения касательных напряжений по высоте прямо- угольного сечения. Для этого найдем сначала выражение для статического мо-

мента (рис. 11.8):
~	~	æ h	öé	1 æ h			öù
Sz (y)= F		(y)yc = bç	- y÷êy +		ç		- z ÷ú	=
						2
		è 2	øë	2 è			øû

	b	æ h	öæ h		ö
=		ç	- y÷ç		+ y÷
	2			2
		è 2	øè		ø

æ h2		ö
ç		- y2 ÷.	(11.19)

ç	4	÷
è		ø

Подставим полученное выражение в формулу Журавского

æ h2

(y)

- y2 ÷

ç 4

= -

- y2 ÷.

(11.20)

Izb

è 4

Отсюда видно,

что закон распределения касательных напряжений по высоте

- 124 -

сечения – квадратная парабола. Если y = ±0,5h , то τxy = 0. Если y = 0, тогда

txy

=1,5

txy ср

(11.21)

max

2 bh

где F – как обычно, площадь всего поперечного сечения.

Таким образом, максимальное касательное напряжение в прямоугольном поперечном сечении в полтора раза превышает среднее значение, вычисленное по простейшей формуле.

Не вполне очевидно, что полученные касательные напряжения в сумме дают перерезывающую силу. В этом легко убедиться, если проинтегрировать (просуммировать) все силы от касательных напряжений. Действительно:

0,5b 0,5h 6Q

æ h2

òtxydF = -

- y

÷dydz =

−0,5b −0,5h bh

æ 0,5b

öé0,5h æ

0,5h

= -

òdz

÷ê ò

ç 4

- y

÷dyú

= -

b ê

y -

3 û

è−0,5b

øë0,5h è

−0,5h

= -

6Qy éh3

h3 ù

= -Qy ,

(11.22)

ë12

12 û

что и требовалось доказать.

	Двутавровое поперечное сечение. Касательные напряжения в бал-
	ках с таким сечением
y	Эп.σx (y)	В прямоугольном сечении слишком
y	Эп.σx (y)	много материала в области малых нор-
		много материала в области малых нор-
		мальных напряжений вблизи нейтрального
z	x	слоя (рис. 11.9). На уровне самого ней-
z	x	трального слоя их нет вообще. Естествен-
		но следует убрать материал из этой зоны и
		добавить в зону действия наибольших
	Mz (x)> 0	нормальных напряжений. Но совсем уб-
	Mz (x)> 0	рать перемычку нельзя. Нечему будет вос-
	Рис. 11.9	принимать касательные напряжения и на-
	Рис. 11.9	пряжения взаимного надавливания про-
		пряжения взаимного надавливания про-
дольных «волокон». Получается характерная форма сечения, изображенная на
рис. 11.9 штриховой линией, – такие сечения называются двутавровыми.
При поперечном изгибе касательные напряжения прямоугольного сече-
ния оказываются, как правило, значительно меньше нормальных. Для воспри-

- 125 -

ятия перерезывающих сил достаточно относительно тонких стенок двутаврово-

го поперечного сечения.

Металлургическая промышленность выпускает стан-

дартный прокат с двутавровой формой сечения. Пропорции

этого симметричного сечения показаны на рис. 11.10. Най-

дем закон распределения касательных напряжений по вы-

соте этого сечения с помощью формулы Журавского. При

этом упростим форму реального двутаврового поперечного

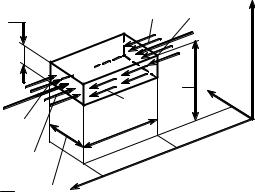
сечения, заменив её тремя прямоугольниками (рис. 11.11).

Использование формулы Журавского не вполне

Рис. 11.10

обосновано для сечения со ступенчато переменной толщи-

ной. Полученный ниже результат следует рассматривать

лишь как оценку закона распределения касательных напряжений.

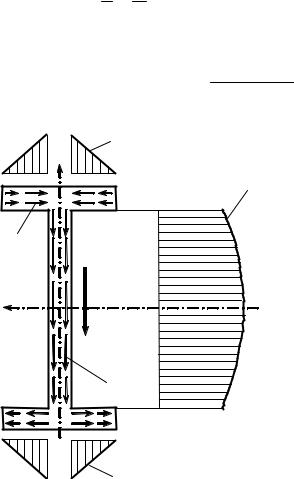
На уровне 1 касательные напряжения получаются нулевыми, поскольку

равна нулю отсеченная площадь (площадь выше рассматриваемого уровня) и

статический момент отсеченной части сечения. До уровня 2 закон будет пара-

болический, если мы считаем, что от уровня 1 до уровня 2 сечение прямоуголь-

ное. На уровне 2 касательное напряжение равно

Эп. τxy (y)

D2 D1

τxy = −

Qy Sz (y2 )

Iz B

D3 D

При переходе из точки 2 в точ-

ку 3

ширина сечения меняется скач-

ком. Касательное напряжение в точке 3

выражается формулой

τxy = −

QySz (y2 )

Qy (x)

Izb

которая

отличается

от

предыдущей

τxy

только заменой B на b в знаменателе. От

этого значение касательного напряже-

ния

возрастает

во столько

же раз, во

сколько B больше b. Ниже точки 3 сече-

Рис. 11.11

ние вновь прямоугольное, поэтому за-

кон изменения τxy

– вновь квадратная парабола, но изменение статического мо-

мента замедляется, поскольку здесь сечение значительно ýже, а следовательно,

уменьшается и наклон параболы. Максимум касательного напряжения по форму-

ле прямоугольного сечения будет при y = 0 на уровне 4. Значение максимального

касательного напряжения зависит, в частности, от толщины стенки двутавра. При

- 126 -

уменьшении этой толщины оно может стать сколь угодно большим, поэтому про-

верка прочности двутавров по касательным напряжениям необходима.

sx (x) C1

Помимо

касательных

напряже-

ний,

по Журавскому, в двутавровом

C 2

N(x, z)

поперечном сечении возникают и дру-

N (x

, z)

гие

касательные напряжения. Будем

рассуждать точно так же,

как и при

tzx

выводе формулы Журавского. Из эле-

мента балки с двутавровым сечением,

sx (x

)

подвергающейся поперечному изгибу,

X +

мысленно выделим элемент XX+ дли-

- z÷

ной dx (рис. 11.1). Затем вертикальным

Рис. 11.12

сечением DD1

(рис. 11.11)

выделим

часть полки DD1D2 D3 и рассмотрим напряжения и силы, действующие на вы-

деленную части полки (рис. 11.12).

Считаем, что t << h . Тогда нормальные напряжения в полке можно счи- тать постоянными в каждом из сечений CC1C2C3 и DD1D2 D3 , а в соседних се-

чениях с координатами x и x+ их можно записать так:

sx (x) = -

M z (x)

sx (x

) = -

M z (x+ )

(11.23)

Умножив напряжения на площадь, по которой они приложены, найдем осевые силы, действующие на выделенную часть полки в направлении оси x

N(x, z)= -

(x)

æ B

(x+ , z)

æ B

× ç

- z ÷t , N(x+ , z) = -

× ç

- z ÷t . (11.24)

è 2

Направления напряжений и сил на рис. 11.12 соответствуют случаю нагруже- ния на рис. 11.1.

Поскольку при поперечном изгибе моменты M z (x) и M z (x+ ) не равны, то не равны и силы N(x, z) и N(x+ , z) . Равновесие выделенного элемента возмож- но только за счёт касательных напряжений τzx в сечении DCC1D2 . Уравнение

равновесия в направлении оси x примет вид
å Xi = 0 = -N(x+ , z)+ N(x, z)+ tzxtdx .						(11.25)
i
Подстановка осевых сил N даёт
dM z (x)		h	æ B	ö
Iz	×	2	×ç	- z ÷t + tzxtdx = 0	,	(11.26)

			è 2	ø

откуда с учетом уравнения равновесия (11.1) находим

	Qy (x)éh			- 127 -
tzx (x, z)= txz (x, z)= -				æ B	ö ù
		ê		× ç	- z ÷tú .	(11.27)
	Izt		2
		ë		è 2	ø û

Если учесть, что выражение в квадратных скобках есть статический момент площади CC1C2C3 или DD1D2 D3 относительно оси z, то, введя для статиче-

ского момента обозначение
ˆ		h	æ B	ö	(11.28)
Sz (z)=		2	×ç	- z ÷t ,	(11.28)
		2	è 2	ø
получим формулу, похожую на формулу Журавского
				ˆ
tzx (x, z)= txz (x, z)= - Qy (x)Sz (z) .					(11.29)
				Izt
			Эп. txz (z)		В отличие от формулы Журав-
	y		Эп. txz (z)		ского статический момент этой форму-
	y			Эп. txy (y)	ского статический момент этой форму-
				Эп. txy (y)	лы изменяется по координате z и меня-
					ется вдоль неё по линейному закону,
					как видно из (11.28). Напряжения τxy
τxz					малы в полках; если пренебречь ими по
z					сравнению с τxz , то распределение ка-
z					сательных напряжений по двутаврово-
	Qy (x)				му сечению принимает вид, показан-
	Qy (x)				ный на рис. 11.13.
					ный на рис. 11.13.
		txy			В стандартных стальных двутав-
		txy			ровых балках напряжения τxz меньше
					напряжений τxy . Но в других случаях
					(например для балки с нестандартным
			Эп.τxz (z)		сечением), напряжения τxz также мо-
			Эп.τxz (z)		гут быть опасны для прочности балки.
		Рис. 11.13			гут быть опасны для прочности балки.
		Рис. 11.13			Из рисунка видно, что касатель-
					Из рисунка видно, что касатель-

ные напряжения как бы обегают тонкостенный контур сечения. Для касатель- ных напряжений в тонкостенных конструкциях характерно, что они действуют вдоль контуров этих сечений. Происходит это потому, что вследствие закона парности касательных напряжений они не могут иметь составляющих, перпен- дикулярных к границе сечения.

- 128 -

Тема №12. Определение перемещений при плоском изгибе стержней. Система дифференциальных уравнений изгиба балки. Про-

верки прочности и жесткости при изгибе

Интегрирование уравнения изогнутой оси балки для определения прогибов и углов поворота поперечных сечений

Для определения перемещений при плоском изгибе следует интегриро-

где v0 (x) – прогибы балки. Индекс 0, использовавшийся для обозначения точки

оси стержня, далее опускаем, поскольку далее рассматриваем перемещения по оси y только этой точки. В этом соотношении v(x) – это единственная неиз- вестная функция, если считать, что эпюра моментов M z (x) уже найдена, а так-

же известна жесткость сечения на изгиб, которую будем для простоты считать постоянной ( EIz = const ).

Так как при малых перемещениях и деформациях
	dv(x)	= θ(x),	(12.2)

	dx
где θ(x) – углы поворота поперечных сечений, то соотношение (12.1)			может

быть записано и так:

EIz dθ(x) = M z (x). (12.3) dx

Интегрирование этого соотношения позволяет с точностью до константы определить углы поворота поперечных сечений балки θ(x):

EIzθ(x)= C + òM z (x)dx .

(12.4)

Подобная операция рассматривалась в задаче чистого изгиба балки. Здесь же рассматривается общий случай плоского изгиба.

Повторное интегрирование даёт прогибы балки v(x)с точностью до двух

констант:
EIzv(x)= D + Cx + ò(òM z (x)dx)dx .	(12.5)

Чтобы точно определить функции θ(x) и v(x), необходимо найти кон- станты интегрирования. Для их определения недостаточно знать производные функций. Нужна дополнительная информация о решении, дополнительные уравнения. Такие уравнения (они называются граничные условия) дают усло- вия опирания балки.

- 129 -

Граничные условия зависят от конкретной задачи. Для балки на плоско- сти с одним участком число вариантов опирания ограничено.

Рассмотрим в качестве примера один из них – балку, изображенную на рис. 11.1. До решения задачи можно записать следующие граничные условия (простейшие уравнения), накладывающие ограничения на искомые функции

перемещений
v(x = l)= 0 ,	(12.6)
θ(x = l)= 0 ,	(12.7)

поскольку в сечении заделки нет прогиба (оно не перемещается вдоль оси y) и нет поворота поперечного сечения. Для задачи на рис. 11.1 выражение изги- бающего момента, получающееся при построении эпюр, имеет вид

M z (x)= Px .

(12.8)

Формулы (12.4) и (12.5) после интегрирования данного выражения для момента будут выглядеть так:

EIzq(x)= C +							Px2			,							(12.9)
EIzq(x)= C +							2			,							(12.9)
							2				Px3
EIzv(x)= D + Cx +											Px3				.		(12.10)
EIzv(x)= D + Cx +															.		(12.10)
												6
Формула (12.9) должна удовлетворять и равенству (12.7), поэтому
EIzq(x = l)= 0 = C +													Pl2			,	(12.11)
EIzq(x = l)= 0 = C +												2				,	(12.11)
												2
откуда находим константу C:
C = -			Pl	2	,												(12.12)
C = -		2			,												(12.12)
		2
Аналогично формула (12.10) должна удовлетворять равенству (12.6):
EIzv(x = l)= 0 = D + Cl +																	Pl3	.
EIzv(x = l)= 0 = D + Cl +																	6	.
																	6
Учтём значение константы C и получим отсюда значение константы D:
D =	Pl2			l -		Pl	3	=	Pl			3		.			(12.13)
D =		2		l -		6		=	3					.			(12.13)
		2				6			3

Окончательные выражения для углов поворота сечений и прогибов балки (рис. 11.1) получаются после подстановки значений констант в (12.9) и (12.10):

q(x)=

(x2 - l2 ) ,

(12.14)

2EIz

EIz è

(2l3 - 3l2x + x3 ) .

v(x)=

x +

(12.15)

6EIz

EIz è

- 130 -
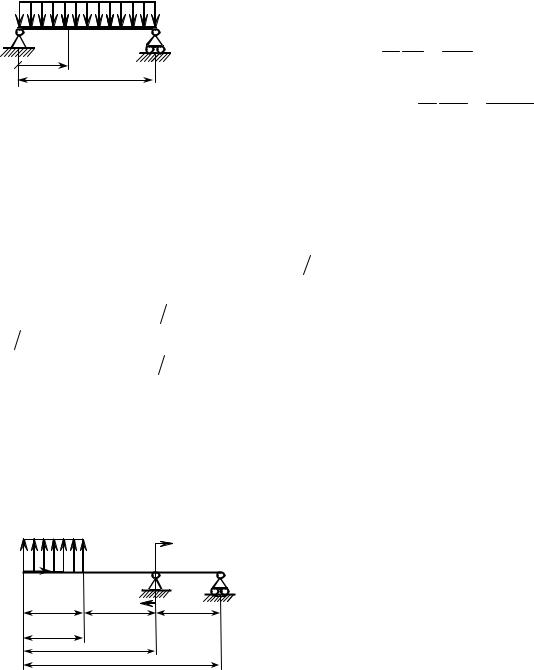
Несколько другие граничные условия получаются для балки, показанной
на рис. 12.1. Прогибы балки на опорах должны быть равны нулю:
v(x = 0)= 0 ,	(12.16)
v(x = l)= 0 .	(12.17)

Оба этих условия накладываются на одну и ту же функцию. Однако и в данном случае несложно найти константы, получающиеся после интегрирования соот- ношения для изгибающего момента в этой задаче:

q	M z (x)= ql x - qx2		,					(12.18)
	2	2
x	EIzq(x)= C + ql x2		- qx3		,			(12.19)
l	2	2	2 × 3
Рис. 12.1	EIzv(x)= D + Cx + ql x3			-		qx4	4	. (12.20)
Рис. 12.1			2 2 ×3			2 ×3×	4

Потребовав, чтобы формула (12.20) удовлетворяла условиям (12.16) и (12.17),

получаем значения констант

EIzv(x = 0)= 0 = D + C × 0 + 0 - 0,

Þ D = 0 ,

(12.21)

EIzv(x = l)= 0 = 0 + Cl +

ql4

Þ C = - ql3 .

(12.22)

2 × 3 × 4

2 2 ×

Нетрудно видеть, что величина C EIz есть угол поворота поперечного се-

чения в точке оси, где размещалось начало координат

q0 = q(x = 0)= C EI z ,

(12.23)

а D EIz – прогиб балки в том же сечении

v0 = v(x = 0)= D EI z .

(12.24)

Можно и по-другому ввести константы при интегрировании (12.3)

q(x)= C +

òM z

(x)dx ,

(12.25)

EIz

ò(òM z (x)dx)dx ,

v(x)= D + Cx +

(12.26)

EIz

тогда

C и D – угол поворота и прогиб в

	q	M
x
I	II	III
l1	l 2
	l 2	l 3
		l 3
	Рис. 12.2

левом торце балки.

Но если в балке несколько участ- ков, то задача существенно усложняется. На каждом участке будет своё выраже- ние для изгибающего момента, а при ин- тегрировании на каждом из участков по- лучится по две константы. Например, в задаче на рис. 12.2 участков три, а кон-

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1813 14 15 16 17 18 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.08.2019341.5 Кб1Lection 3.doc
#
18.08.2019195.58 Кб3Lection 5.doc
#
18.08.2019239.1 Кб2Lection 6.doc
#
04.11.2018179.83 Кб6lections.docx
#
15.04.2019980.99 Кб4lecton.DOC
#
12.03.20151.35 Mб41Lectures part1.pdf
#
12.03.20151.33 Mб21Lectures part2.pdf
#
26.04.20191.77 Mб5lekcii_po_nachertatelnoy_geometrii.doc
#
16.04.201983.46 Кб1Lektsia_16 (1).doc
#
15.08.201959.39 Кб1lektsia_1_Sistema_stimulirovania_kak_chast_sist...doc
#
16.04.201958.88 Кб4Lektsia_23 (1).doc