2.2. Передаточные функции

2.2.1. Символическая запись дифференциальных уравнений и передаточных функций

Уравнение (2.8) удобнее записывать в символической форме, вводя алгебраизированный оператор дифференцирования p=d/dt. Тогда любая производная уравнения (2.8) может быть выражена символьной формулой

(2.9)

а уравнение (2.8) примет вид:

(2.10)

Считая условно оператор дифференцирования p=d/dtалгебраической величиной, преобразуем уравнение (2.10) к виду:

(2.11)

где

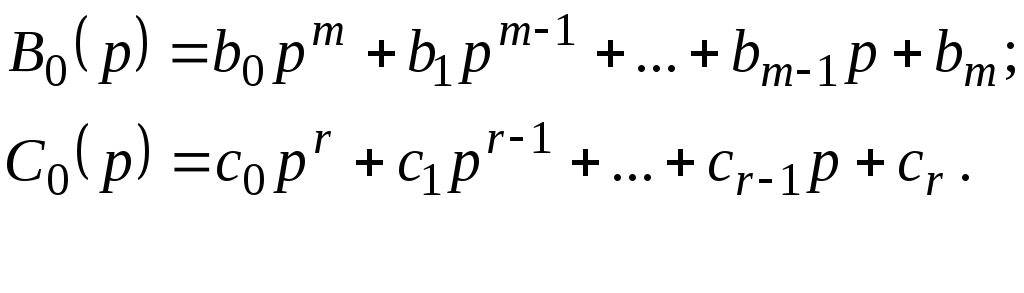
Полином A₀(p) представляет собой характеристический полином исследуемой системы (или её отдельного звена). Он характеризует свободное движение системы, т.е. её движение приu=0 иf=0 под влиянием ненулевых начальных значенийвызванных, например, исчезнувшим к моменту времениt=0 возмущающим воздействиемf(t). В зависимости от знаков вещественных частей корней уравненияA₀(p) система может быть устойчивой или неустойчивой.

Полином B₀(p) определяет влияние управляющего воздействияu(t) на характер изменения управляемой величиныy(t).

Полином C₀(p) определяет влияние возмущающего воздействияf(t) на характер изменения управляемой величины.

Решим уравнение (2.11) относительно выходной величины:

(2.12)

Выражения

(2.13)

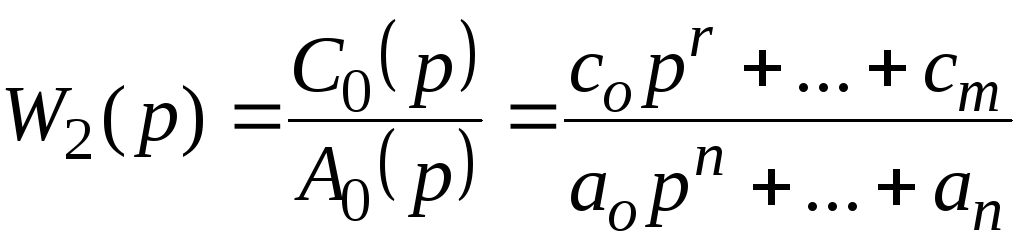(2.14)

называются в теории автоматического управления передаточными функциями.

Выражения (2.10), (2.11), (2.12) представляют собой символическую запись дифференциального уравнения (2.8). Переменные в этих уравнениях остаются функциями времени. Чтобы подчеркнуть это, выражение (2.12) можно записать так:

(2.15)

Передаточные функции (2.13), (2.14) вводятся для сокращения символической записи дифференциальных уравнений. Более строго передаточная функция определяется через изображения Лапласа.

2.2.2. Определение передаточных функций через изображения Лапласа

Преобразованием Лапласа или изображением переменной x(t), такой, чтоиназывается комплекснозначная функция, определяемая интегралом

(2.16)

где - комплексная переменная, вещественная часть которойσпредставляет собой так называемую абсциссу абсолютной сходимости. Для большинства функций, с которыми приходится иметь дело в управлении, абсцисса абсолютной сходимости равна нулю.

Функцию времени x(t) по которой найдено изображениеназывают оригиналом.

Отыскание изображения функции x(t) с помощью интеграла (2.16) называют прямым преобразованием Лапласа и условно обозначают его выражением

(2.17)

Умножим уравнение (2.8) на функцию и проинтегрируем его по времени от нуля до бесконечности.

Преобразование Лапласа обладает свойством линейности:

(2.18)

поэтому в левой и правой частях уравнения (2.8) будут суммы интегралов:

(2.19)

Согласно формуле (2.16) обозначим:

(2.20)

Найдем изображение первой производной.

(2.21)

Применим к (2.21) правило интегрирования по частям. Обозначим: Тогда(2.22)

Применяя такой же метод для нахождения изображения второй производной, получим формулу:

(2.23)

Для изображения k- ой производной на основании формул (2.22) и (2.23) нетрудно найти выражение

(2.24)

Полагая все начальные условия нулевыми, запишем уравнение (2.19) в виде:

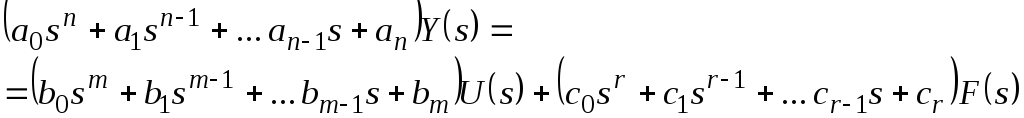(2.25)

Уравнение (2.25) можно записать как и уравнение (2.11) в виде

где полиномы имеют такой же смысл, как и полиномы.

Решим уравнение (2.25) относительно изображения выходной величины:

(2.26)

где 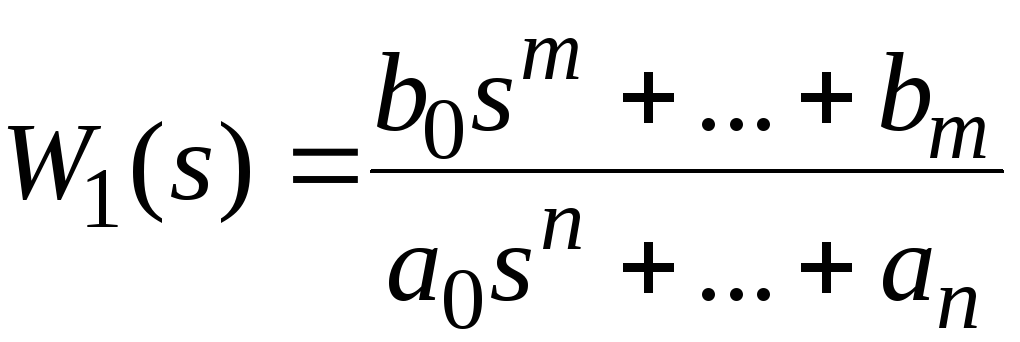(2.27)

• передаточная функция САУ по отношению к входной величине u(t);

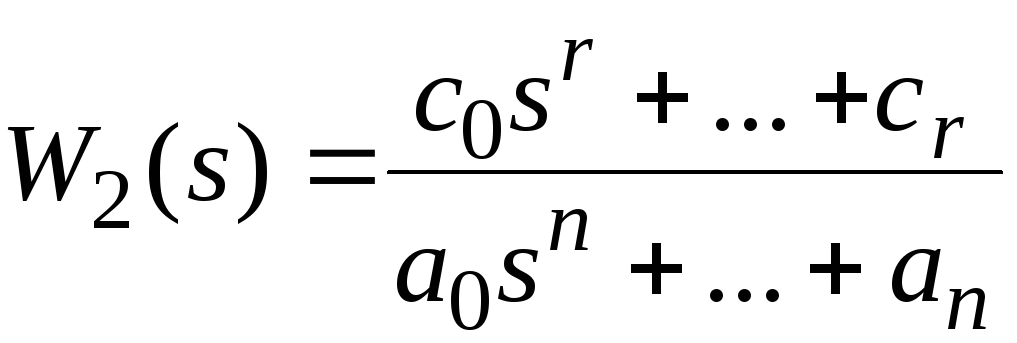(2.28)

• передаточная функция САУ по отношению к возмущающему воздействию f(t).

Если возмущающее воздействие f(t)=0, тоY(s)=W₁(s)U(s) иW₁(s)=Y(s)/U(s) (2.29)

Если равна нулю входная величина u(t)=0, тоY(s)=W₂(s)F(s) иW₂(s)=Y(s)/F(s) (2.30)

Согласно выражениям (2.29), (2.30) передаточной функцией линейной стационарной динамической системы по отношению к некоторому входному воздействию называют отношение изображения Y(s) величиныy(t) на выходе системы к изображению входного воздействия, которые получены прямым преобразованием Лапласа при нулевых начальных условиях.