12.2. Частотный критерий Найквиста

Чтобы построить АФХ разомкнутой системы, можно использовать преобразование z=e^Ts. Положив, получим

(12.3)

Подставив (12.3) в выражение для передаточной функции разомкнутой системы W(z), найдем частотную передаточную функцию разомкнутой системы. Определив модуль и фазу или вещественную и мнимую части этой функции, можно построить АФХ разомкнутой системы.

Следует учитывать, что функция (12.3) периодическая. Поэтому при построении АФХ достаточно ограничиться диапазоном частот .

Построим АФХ разомкнутого дальномера из примера 1 раздела 11.2. Передаточная функция разомкнутой системы найдена в виде .

В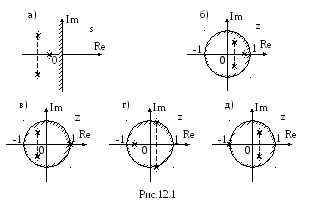результате замены (12.3) получим

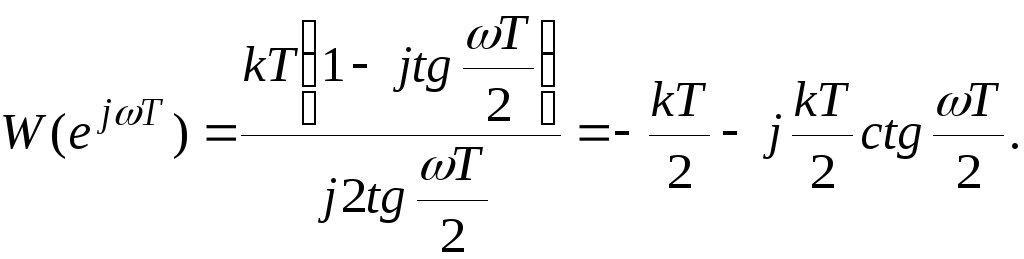(12.4)

АФХ разомкнутой системы изображена на рис.12.2а. Так как при =0 она имеет разрыв, обусловленный наличиемsв знаменателе, дополняем ее четвертью окружности бесконечно большого радиуса. Для исследования устойчивости замкнутой системы можно использовать формулировку критерия Найквиста, соответствующую данному случаю (см. раздел 7.5), а именно: замкнутая система будет устойчива, если АФХ разомкнутой системы не охватывает точку (-1;j0). Следовательно, как видно из рис. 12.2а, замкнутая система устойчива приkТ< 2. В соответствии со второй формулировкой сумма переходов АФХ через критический отрезок (‑; ‑1) должна быть равна нулю. ПриkТ< 2 переходов нет и замкнутая система устойчива. ПриkТ>2 АФХ заканчивается на критическом отрезке, т.е. имеет место –1/2 перехода.

При использования преобразования z=e^jTчастотная передаточная функцияW(e^jT) является трансцендентной (т.е. не алгебраической функцией частоты, а, в данном случае, тригонометрической). Поэтому для систем выше второго порядка построение АФХ существенно затрудняется. Кроме того, практически исключается возможность построения асимптотических ЛЧХ.

Преобразование (12.3) можно приближенно заменить алгебраической функцией для значений аргумента тангенса T/2<1, т.е. для частот в диапазоне 0<2/T. В этом случае можно принять, чтоtg(T/2) T/2, тогда формула (12.3) примет вид

(12.5)

По аналогии с (12.5) используют так называемое билинейное преобразование, заменяя новой переменной:

(12.6)

Переменная λназывается абсолютной псевдочастотой, сокращённо-псевдочастотой. Сравнив (12.6) с (12.3), получим:

(12.7)

Из (12.7) видно, что благодаря сомножителю 2/Tпсевдочастотаλимеет размерность угловой частоты. Кроме того, при измененииωот 0 доπ/Tона изменяется от нуля до бесконечности. Наконец, приω<2/Tпсевдочастота практически совпадает с реальной частотойω.

При исследовании устойчивости и качества импульсных систем можно оперировать с jλточно так же, как это делалось сjωили сsпри исследовании непрерывных систем.

В качестве примера используем подстановку (12.6) в передаточной функции . В результате получим частотную передаточную функцию разомкнутой системы:

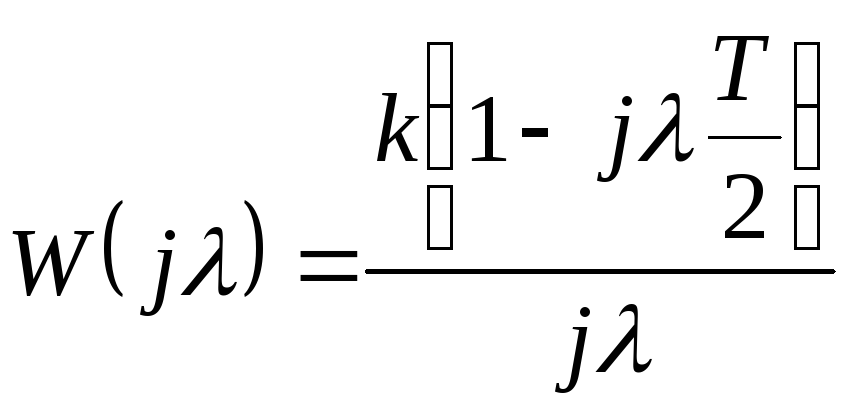(12.8)

Амплитудную частотную характеристику определим как модуль вектора W(jλ):

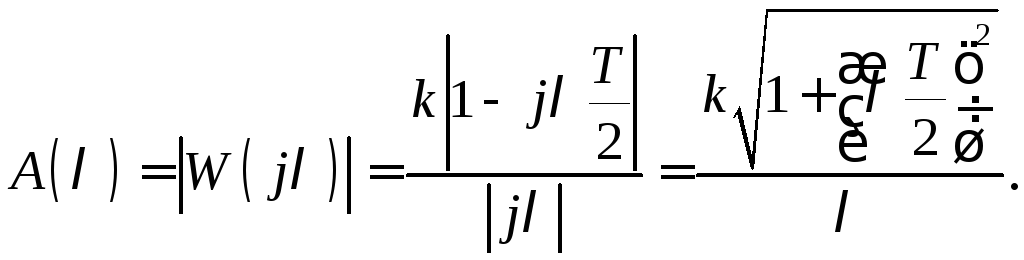(12.9)

Логарифмическую амплитудную характеристику запишем в виде

, (12.10)

где (12.11)

. (12.12)

Как видно из выражений (12.11), (12.12), ЛАХ L₁(λ) совпадает с ЛАХ интегрирующего звена (4.24), а ЛАХL₂(λ) – с ЛАХ дифференцирующего звена первого порядка (4.14). Таким образом, графикL₁(λ) есть прямая с отрицательным наклоном 20 дб/дек, пересекающая ось абсцисс приλ=k. ГрафикL₂(λ) состоит из двух асимптот с точкой сопряжения на частотеλ=2/T. Горизонтальная асимптота до частотыλ=2/Tсовпадает с осью абсцисс, а вторая асимптота имеет положительный наклон 20 дб/дек.

График асимптотической ЛАХ L(λ) совпадает с графикомL₁(λ) до сопрягающей частотыλ=2/T, где, получив излом на +20 дб/дек, переходит в горизонтальную прямую (рис. 12.2 б).

Для определения фазовой частотной характеристики преобразуем функцию (12.8) к виду:

,

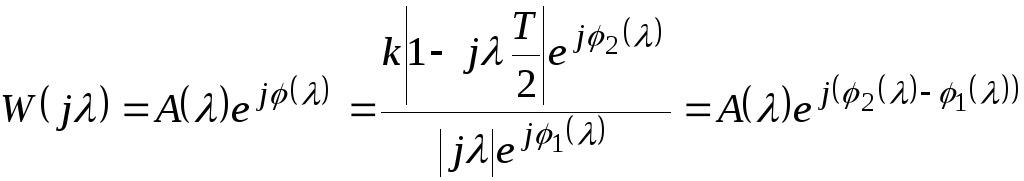где

Графики L(λ) иφ(λ) показаны на (рис. 12.2 б). Еслиk<2/T, то горизонтальная асимптота проходит ниже оси абсцисс. При этом критический отрезок, соответствующий значениямA(λ)≥1, находится левее частоты среза, то есть левее точкиλ=k, и ЛФХ в этом интервале частот не пересекает линии -180⁰. Следовательно, замкнутая система устойчива. Если жеk>2/T, то вторая асимптота проходит выше оси абсцисс и критическим отрезком будет вся эта ось. При фазаφ(λ)=-180⁰, аL()>0 (A(λ)>1). Следовательно, имеет место -1/2 перехода и замкнутая система неустойчива.

Нетрудно убедиться, что АФХ разомкнутой системы

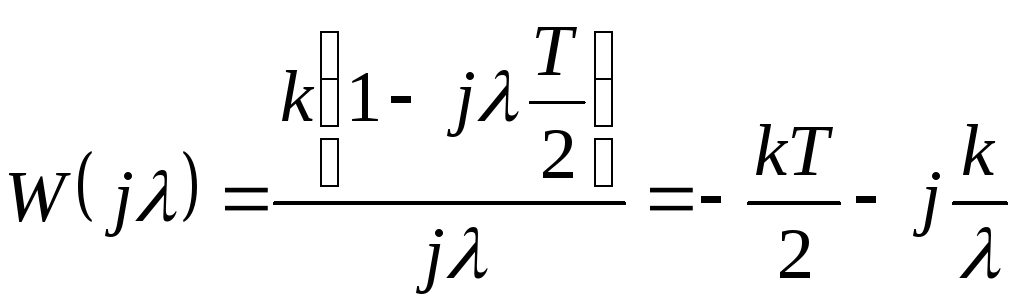
будет точно такой же, как на рис. 12.2 а, только она закончится на оси абсцисс при λ=.