6.2. Управляемость и наблюдаемость

Постановка задачи

Дана линейная многомерная стационарная система управления, поведение которой описывается уравнениями состояния и выхода:

(6.19)

где -n– мерный вектор состояния;

-r– мерный вектор управления;

- время,- промежуток времени функционирования системы;

- мерный вектор выхода;

- матрицы размерасоответственно;

- начальное состояние.

Система (6.19) называется полностью управляемой, если существует такое управляющее воздействие определенное на конечном интервале временикоторое переводит систему из любого начального состоянияв любое заданное конечное состояние.

Система (6.19) называется полностью наблюдаемой, если по реакции на выходе системы на промежутке временипри заданном управляющем воздействииможно определить начальное состояние.

Постановка задачи формулируется следующим образом.

Пусть известны матрицы системы (6.19). Требуется определить, является ли система полностью управляемой и наблюдаемой.

Критерии управляемости и наблюдаемости.

Условия управляемости для системы, описываемой уравнениями (6.19), определяются следующим критерием, полученным Калманом.

Необходимое и достаточное условие для управляемости системы (6.19) заключается в том, чтобы матрица

(6.20)

имела ранг, т.е. число линейно независимых строк, равный размерности вектора состояния:

Необходимые и достаточные условия для полной наблюдаемости состоят в том, чтобы матрица

(6.21)

имела ранг, равный размерности вектора состояния:

Замечание: если линейная стационарная система управления описывается уравнениями

то, вводя обозначения дифференциальные уравнения системы можно записать в эквивалентной форме:

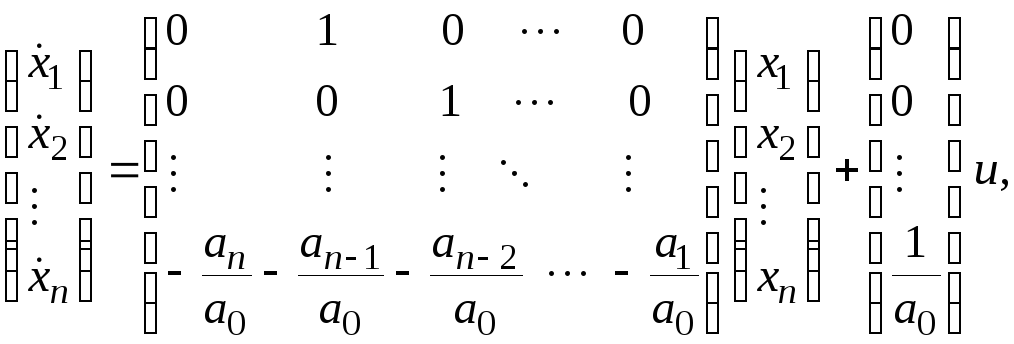
Пример определения управляемости и наблюдаемости системы

Исследовать управляемость и наблюдаемость системы:

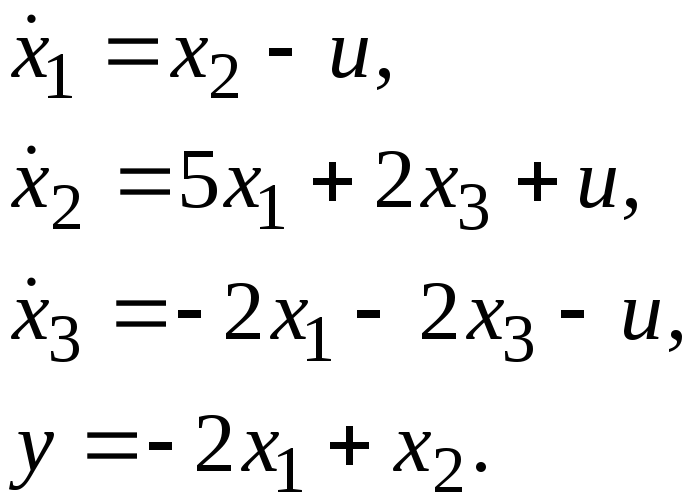
1. В уравнениях состояния и выхода выделим матрицы A, B, C:

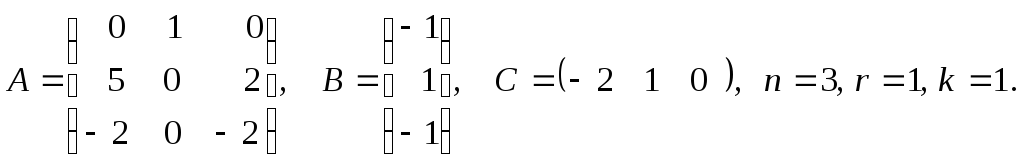
2. Составляем матрицы управляемости и наблюдаемости:

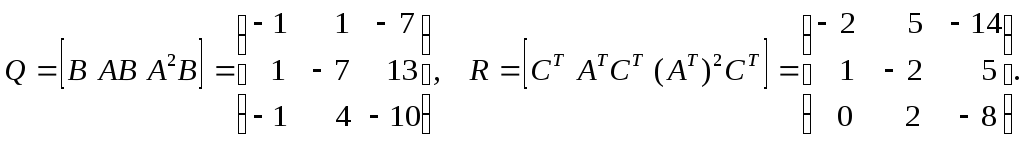
3. Определяем ранги матриц путем приведения их к треугольной форме методом Гаусса:

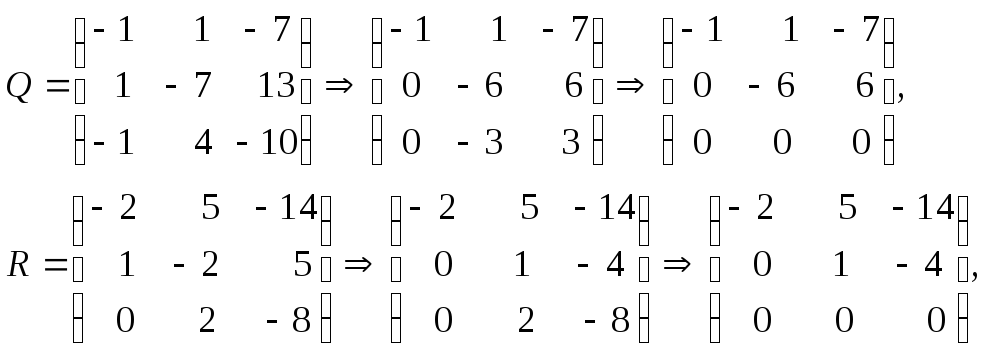
Вывод: система не является полностью управляемой и наблюдаемой.

Понятия управляемости и наблюдаемости важны, например, тогда, когда алгоритм управления формируется не в зависимости от ошибки системы, а в функции переменных состояния:

Однако, в изложенном выше смысле они не всегда совпадают с практическими представлениями. Даже если какая-либо переменная состояния и может быть вычислена по доступным для измерения выходным величинам, обработка этих величин, особенно при наличии помех, может быть сложной. Поэтому практически наблюдаемыми переменными обычно считаются те из них, которые могут быть непосредственно измерены теми или иными датчиками.

Тема 7. Устойчивость линейных непрерывных сау

7.1. Основные понятия об устойчивости

Пусть уравнения состояния системы, характеризующие ее свободное движение, представлены системой нелинейных дифференциальных уравнений

(7.1)

где - обобщенные координаты системы, т.е. переменные, описывающие ее состояние;

- известные функции, определенные в некоторой фиксированной области пространства переменных.

Пусть величины обозначают начальные значения переменных.Каждой системе начальных значенийсоответствует решение уравнений (7.1)

(7.2)

Среди решений (7.2) имеется так называемое очевидное решение уравнений (7.1), характеризующее установившийся процесс, когда переменные состояния принимают постоянные значения

(7.3)

Если подставить решение (7.3) в дифференциальные уравнения (7.1), то левые части уравнений обратятся в ноль. Тогда решение (7.3) можно получить как корни уравнений

(7.4)

Решение (7.3) входит в семейство решений (7.2) и определяется начальными условиями(7.5)

Введем отклонения координатот установившихся значений:

(7.6)

Подставляя в уравнения (7.1) значения обобщенных координат

получим:

(7.7)

Так как постоянные величины, в правой части уравнения (7.7) записана функция переменных:

;(7.8)

Подставив обозначения (7.8) в уравнения (7.7), получим уравнения возмущенного движения:

(7.9)

Формула (7.6) определяет преобразование переноса начала координат в точку

(7.10)

Решению (7.3) в пространстве координат соответствует решение(7.11)

По терминологии А.М. Ляпунова уравнения (7.11) называют невозмущенным движением системы.

При переменныепринимают начальные значения, которые называют возмущениями. Каждой заданной системе таких возмущений отвечает однозначное и непрерывное решениеуравнений (7.9). Это решение называют возмущенным движением системы.

В большинстве задач теории автоматического управления функции допускают разложение в степенные ряды, сходящиеся в некоторойH-окрестности начала координат (7.11):

если достаточно мала. В этих случаях уравнениям (7.9) можно придать вид

(7.12)

где - постоянные коэффициенты, полученные как значения частных производных функцийпо переменным, вычисленные при нулевых значениях переменных;функции, содержащие члены второго и выше порядка малости.

На практике судят об устойчивости решения (7.11), рассматривая лишь уравнения, называемые уравнениями 1-го приближения вместо уравнений (7.12):

(7.13)

А.М. Ляпунов показал, что все случаи исследования уравнений (7.13) следует разделять на категории некритических и критических случаев. К категории некритических относятся случаи, в которых вопрос об устойчивости (или неустойчивости) невозмущенного движения однозначно разрешается на основании исследования уравнений 1-го приближения (7.13).

Запишем уравнения (7.13) в векторно-матричной форме:

(7.14)

где - вектор состояния;

- квадратная матрица.

Характеристическое уравнение системы (7.13)

(7.15) приводится к виду

(7.16)

Пусть все корни уравнения (7.16) различны. Тогда решение уравнения (7.15) для переменной x_iимеет вид:

(7.17)

где - корни характеристического уравнения;- постоянные интегрирования, зависящие от начальных условий.

Пусть - вещественный корень. Еслито членс течением времени непрерывно возрастает и стремится к бесконечности. В этом случаетакже стремится к бесконечности и система неустойчива.

Если то членс течением времени стремится к нулю.

Пусть один из корней - комплексный, тогда всегда существует сопряженный с ним:

(7.18)

В этом случае константы интегрирования также будут комплексно-сопряженными величинами:

(7.19)

Составляющая решения (7.17), соответствующая корням (7.18), имеет вид:

(7.20)

Обозначим где- угол фазового сдвига. Окончательно решение (7.20) примет вид:

(7.21)

Если то имеют место колебания с частотойи нарастающей амплитудой – движение неустойчиво.

Если получим незатухающие колебания – система на границе устойчивости.

Если то амплитуда колебаний с течением времени уменьшается – колебания затухают.

Отсюда можно сделать следующие выводы:

- если все вещественные части корней характеристического уравнения отрицательны, то система устойчива;

- если хотя бы один из корней имеет положительную вещественную часть, то система неустойчива.

- если среди корней характеристического уравнения имеется один или несколько нулевых корней, а вещественные части остальных корней отрицательны, то говорят, что система нейтрально устойчива. Этот случай называют критическим и для определения устойчивости системы требуется специальное исследование нелинейных членов разложения.