7.2. Общая характеристика критериев устойчивости

Критериями устойчивости называют правила, которые позволяют определить устойчивость системы без вычисления корней характеристического уравнения.

Критерии устойчивости можно разбить на две группы: алгебраические и частотные. К алгебраическим критериям относят критерий устойчивости Рауса и критерий устойчивости Гурвица. Эти критерии для систем, описываемых дифференциальными уравнениями выше 4-й степени, дают лишь возможность определить, устойчива ли система. Но их применение для определения изменения параметров системы с тем, чтобы сделать ее устойчивой, затруднительно.

Частотные критерии могут быть разделены на две подгруппы:

1. Исследуется непосредственно замкнутая система (критерий устойчивости Михайлова).

2. Об устойчивости замкнутой системы судят по частотным характеристикам разомкнутой системы (критерий устойчивости Найквиста).

Достоинством частотных критериев является наглядность и возможность использования частотных характеристик, полученных экспериментально. Во многих случаях частотные критерии устойчивости дают представление о качестве процесса регулирования.

7.3. Критерий устойчивости Гурвица

Этот критерий был сформулирован в 1895 году математиком А. Гурвицем.

Для характеристического уравнения (7.16) составим квадратную матрицу коэффициентов, содержащую nстрок иnстолбцов:

(7.22)

Эта матрица составляется следующим образом.

По диагонали от левого верхнего до правого нижнего углов записывают все коэффициенты по порядку от до. Каждая строка дополняется коэффициентами с нарастающими индексами слева направо так, чтобы чередовались строки с нечетными и четными индексами. В случае отсутствия коэффициента, а также, если индекс его должен быть меньше нуля или больше n, на соответствующем месте в матрице (7.22) пишут нуль.

Критерий устойчивости сводится к тому, что при должны быть больше нуля всеnопределителей Гурвица, получаемых из квадратной матрицы коэффициентов. Обозначим определители Гурвица символами

Индексы определителей Гурвица указывают их порядок, а также индекс диагонального коэффициента матрицы (7.22), который занимает место в правом нижнем углу соответствующего определителя Гурвица.

Условия устойчивости по критерию Гурвица записываются в виде:

;….;

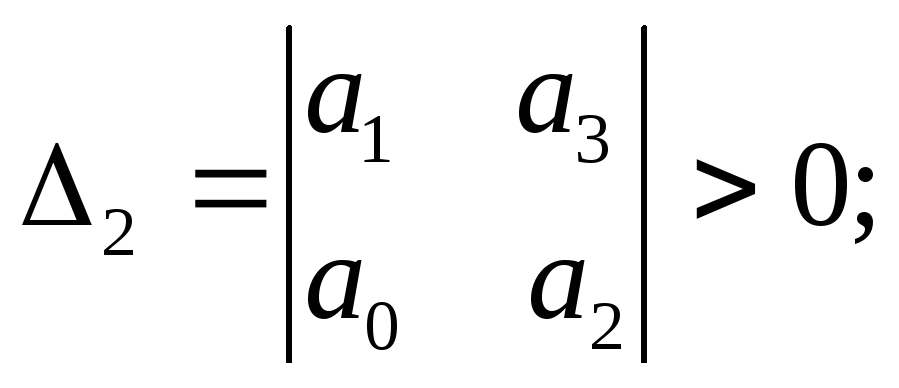
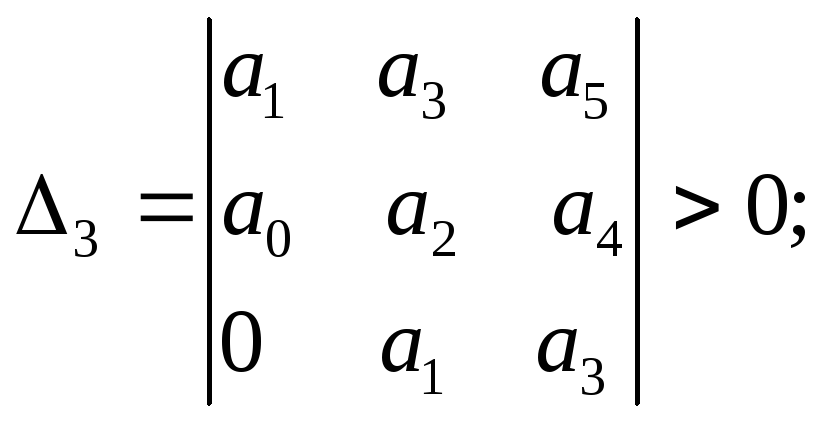Последний определитель включает в себя всю матрицу. Но так как в последнем столбце матрицы все элементы, кроме нижнего, равны нулю, то последнее неравенство запишем в виде:

Так как предыдущее неравенство имеет вид то условие положительности определителя, сводится к условию

Таким образом, критерий Гурвица формулируется следующим образом: для того, чтобы система была устойчива, необходимо и достаточно, чтобы при определители Гурвицабыли положительными.

Необходимые, но недостаточные, условия устойчивости заключаются в том, что в случае уравнения n-го порядка все коэффициентыдолжны быть положительны и ни один из них не должен равняться нулю.

7.4. Принцип аргумента

Рассмотрим алгебраическое уравнение n-й степени с действительными коэффициентами:

Если через обозначить корни этого уравнения, то многочленможно представить в виде произведения простых сомножителей:

На комплексной плоскости каждому корню соответствует вполне определенная точка. Геометрически каждый кореньможно изобразить в виде вектора, проведенного из начала координат к точке (где- вещественная часть корня, а- мнимая (рис. 7.1 а).

Если положить вто

(7.23)

Изобразим на комплексной плоскости элементарный вектор(рис. 7.1 б). Этот вектор является разностью двух векторов: вектораи вектораКонцы элементарных векторовнаходятся на мнимой оси в точке, а начала – в точках с координатами. При измененииот 0 доконцы векторовскользят по мнимой оси, а векторыпри этом поворачиваются. Направление вращения вектора против часовой стрелки с ростомпринимают за положительное. Если начало векторалежит в левой части комплексной плоскости (вещественная часть корня_iотрицательная), то при измененииот 0 довекторвращается в положительную сторону и изменение его аргумента

Для всех корней

Начальные значения аргументов векторов различны в зависимости от четырёх возможных вариантов расположения корней на комплексной плоскости (рис. 7.2). Найдем изменение аргумента элементарных векторовпри измененииот 0 додля приведённых на рис.7.2 вариантов расположения корней.

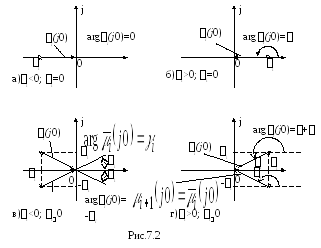
Вариант 1. Вещественный корень в левой части КП.

Вариант 2. Вещественный корень в правой части КП.

Вариант 3. Пара комплексно-сопряженных корней в левой части КП.

Векторы изапишем в показательной форме:

,

где

В выражении для полинома векторыиявляются сомножителями. Запишем формулу для произведения векторови:

Найдем изменение аргумента произведения векторов ипри измененииот 0 до:

.

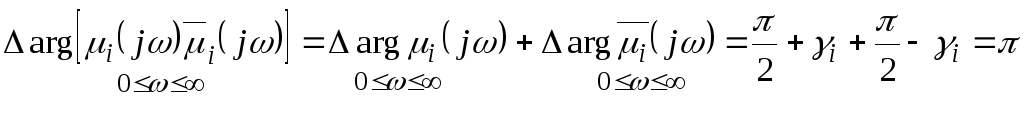Вариант 4.Пара комплексно-сопряженных корней в правой части КП.

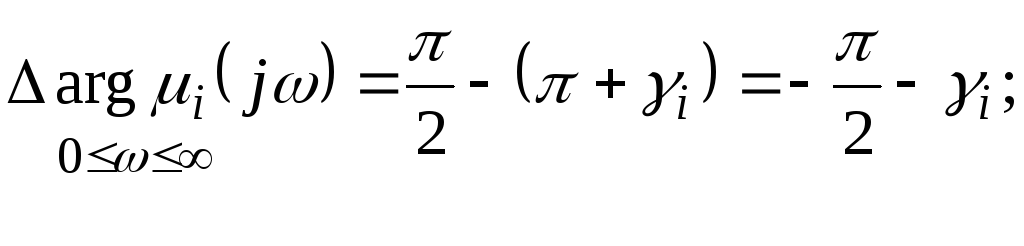
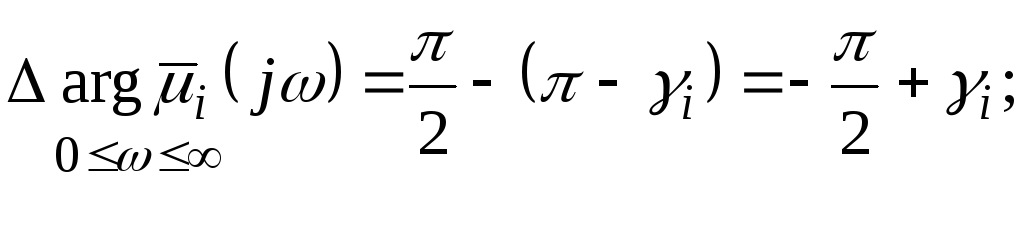
По аналогии вариантом 3 найдем изменение аргумента произведения векторов ипри измененииот 0 до:

.

Запишем выражение для вектора (см. (7.23)).

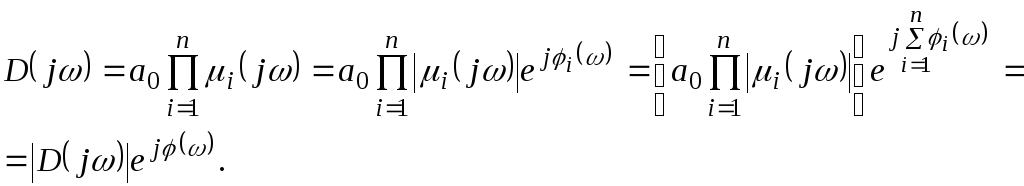
Аргумент (или фаза) вектора равен сумме аргументов элементарных векторов:

Предположим, что уравнение =0 имеетmкорней в правой части КП и, следовательно,n-mкорней в левой части КП. Пусть при этомqправых корней иrлевых корней – вещественные. Тогда в правой части КП количество пар комплексно-сопряженных корней будет равно (m-q)/2 а в левой (n-m-r)/2 При возрастанииот 0 доизменение аргумента вектораили угол поворотабудет

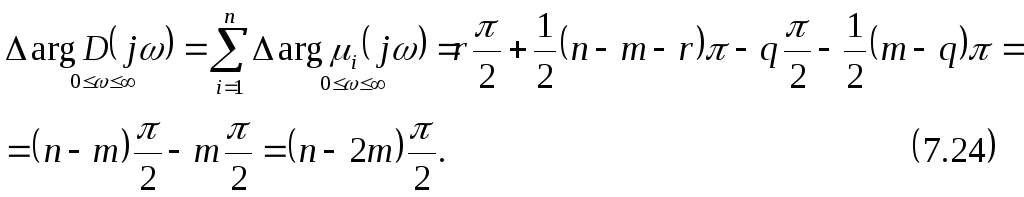
Если все корни уравнения =0 находятся в левой части КП, то