4.2. Типовые динамические звенья второго порядка

В общем случае дифференциальное уравнение звена второго порядка можно записать в виде:

. (4.45)

Символическая запись уравнения (4.45):

(4.46)

Данное уравнение имеет смысл анализировать лишь в случае, когда полиномы, заключенные в скобки, не имеют вещественных корней и не могут быть разложены на более простые сомножители. С этой точки зрения уравнением (4.45) можно описать динамику двух типовых звеньев.

4.2.1. Колебательное звено Колебательное звено имеет передаточную функцию

(4.47)

где Т_k– постоянная времени,- коэффициент демпфирования,k– передаточный коэффициент. Уравнение колебательного звена получим из (4.45) при(4.48)

где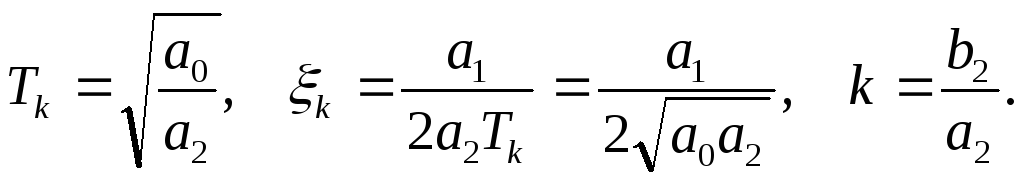

Чтобы корни характеристического уравнения

(4.49)

были комплексно-сопряженными, коэффициент демпфирования должен находиться в интервале 0<_k<1. При=0 получим так называемое консервативное звено с передаточной функцией

(4.50)

Такая система не рассеивает энергии и в ней протекают незатухающие колебания. Если >1, то звено может быть представлено в виде двух последовательно соединенных апериодических звеньев с различными постоянными времени, если=1, то апериодические звенья имеют одинаковые постоянные времени.

В качестве примера колебательного звена рассмотрим RLС-цепочку (рис. 4.10).

По второму закону Кирхгофа: (4.51)

где

Исключая промежуточные переменныеприведём уравнение (4.51) к виду:

(4.52)

Уравнение (4.52) совпадает с (4.48) при k=1,

Характеристики звена:

а) Переходную характеристику колебательного звена находим как решение дифференциального уравнения (4.48) при нулевых начальных условиях и входном воздействии

Решение уравнения (4.48) есть сумма решения однородного уравнения

(4.53)

и частного решения уравнения (4.48), которое здесь можно считать константой, равной

Однородному уравнению (4.53) соответствует характеристическое уравнение

(4.54)

корни которого при условии комплексно-сопряжённые:

(4.55)

Обозначим: Величинуназывают частотой недемпфированных колебаний или собственной частотой. Величинаназываемая декрементом колебаний, показывает скорость изменения амплитуды колебаний со временем, а величинаесть частота свободных колебаний выходной величины.

Решение уравнения (4.48) может быть записано так:

(4.56)

Продифференцируем выражение (4.56) по времени:

(4.57)

Подставив в (4.56) и (4.57) начальные условия, получим:

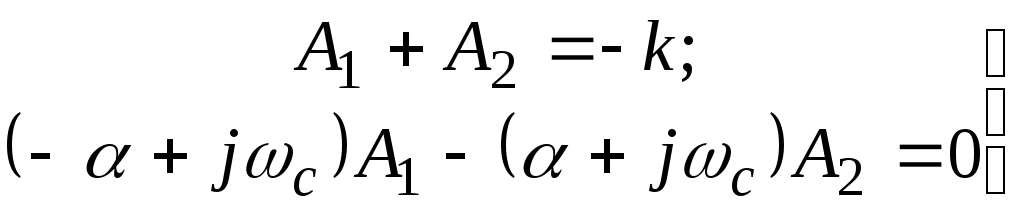(4.58)

Из уравнений (4.58) находим константы интегрирования А₁и А₂:

(4.59)

Подставив (4.59) в выражение (4.56), получим переходную функцию колебательного звена:

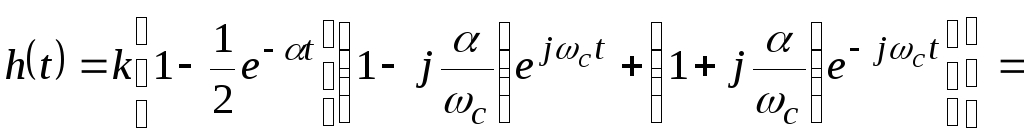
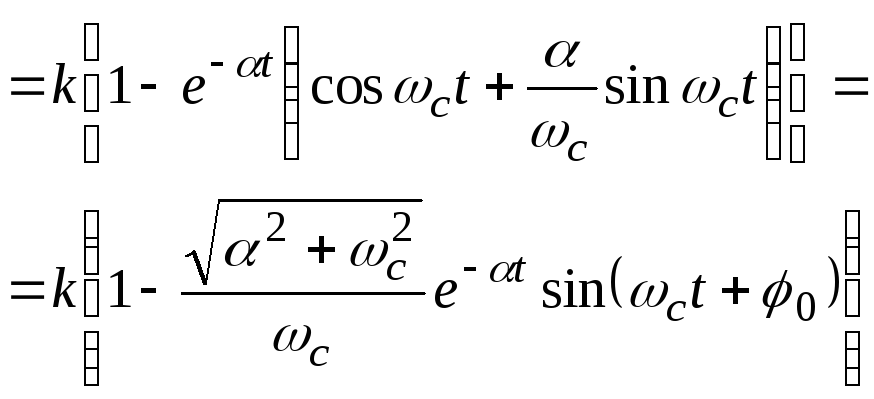(4.60)

где

В первоначальных обозначениях решение (4.60) примет вид:

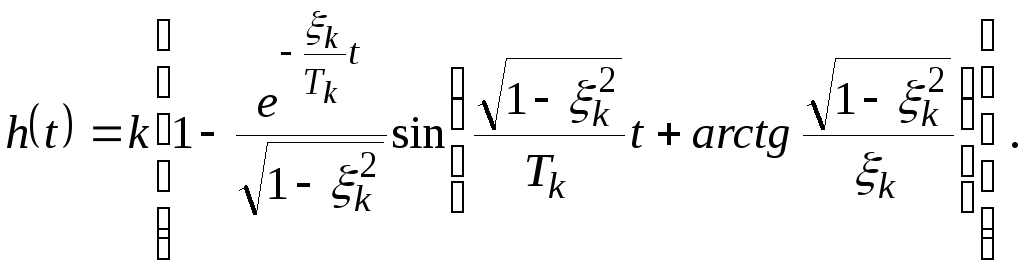(4.61)

В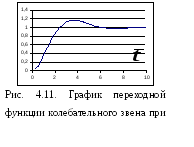качестве примера на рис. 4.11 изображен график переходной функции колебательного звена для случаяиk=1

где.

б) Частотные характеристики колебательного звена имеют вид

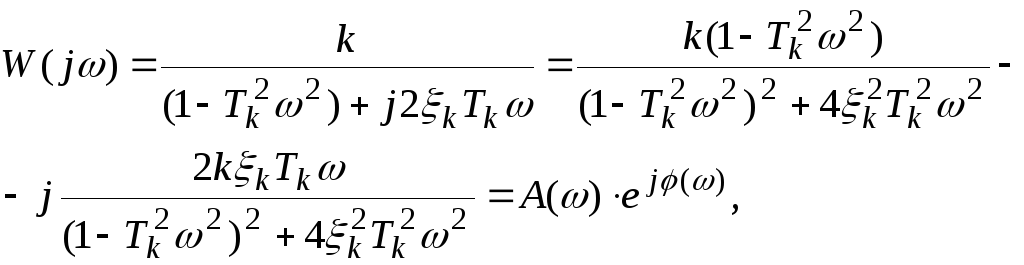(4.62)

где АЧХ: (4.63)

ФЧХ: 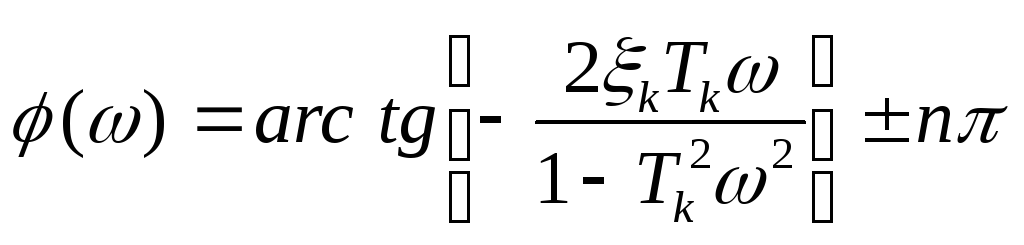. (4.64)

Из выражения (4.64) видно, что при изменении частоты от 0 до в точке=_a=1/T_k аргумент функцииarctgтерпит разрыв 2-го рода. Так какесть непрерывная функция частоты, построение ФЧХ следует выполнять по формулам:

(4.65)

АФХ звена показана на рис. 4.12. Она начинается на действительной оси в точке kприПри частотекривая подходит к началу координат и касается действительной оси. При этом векторприближается к отрицательному направлению вещественной оси. Выходная величина при частотеотстает от входной на 180.

в) ЛАХ колебательного звена описывается выражением

(4.66)

При значениях частоты <1/T_kи>1/T_kЛАХ (2.116) может быть приближенно заменена прямыми линиями (асимптотами)

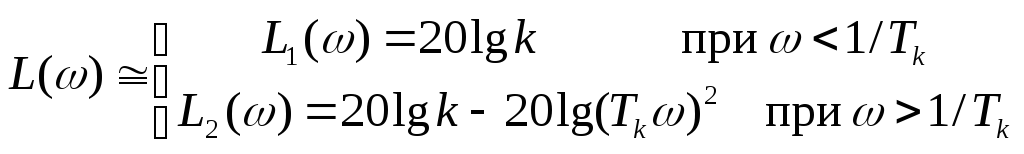
ЛАХ колебательного звена при малых асимптотически стремится к прямойимеющей нулевой наклон, а при большихасимптотически стремится к прямойимеющей наклон – 40 дБ на декаду:

Кривые в зависимости от величинымогут иметь существенный пик при

т.е. при величина пика по сравнению с величиной асимптотической ЛАХравна. Например, припик составляет 0 дБ, а привеличина пика равна 20 дБ. График ЛФХ строят по формулам (4.65).

На рис. 4.13 приведены графики ЛАХ и ЛФХ для значений ,k=1, а по оси частот отложены значения нормированной частоты.