1.6. Классификация задач теории автоматического управления

В общем случае работу системы автоматического управления определяют три основных компоненты (рис. 1.9):

1. входное воздействие g(t), задающее программу работы САУ;

2. управляемая величина y(t), которая должна удовлетворять предъявляемым к ней требованиям;

3. оператор системы W, являющийся математической моделью САУ.

В соответствии с этим задачи расчета систем управления делятся на три группы:

1. Задачи анализа: по заданному входному воздействию и оператору системы исследовать закон изменения управляемой величины.

2. Задачи синтеза: по желаемому закону изменения управляемой величины найти входное воздействие.

3. Задачи идентификации: по входному и выходному сигналам определить оператор системы.

Тема 2. Математическая модель непрерывной линейной сау

2.1. Линеаризация уравнений

Пусть динамическое уравнение некоторой САУ (или ее отдельного звена) имеет произвольный нелинейный вид

, (2.1)

где y– выходная величина;u– входная величина;f– внешнее возмущение;.

Допустим, что установившийся процесс в системе имеет место при некоторых постоянных значениях переменных u = u^*, f = f^*, y = y^*. Тогда уравнение установившегося состояния согласно (2.1) будет

(2.2)

В возмущенном движении переменные, являющиеся аргументами функций Fиуравнения (2.1), будут отличаться от своих установившихся значений:

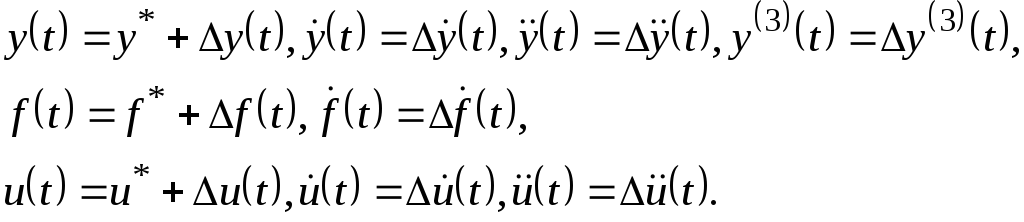(2.3)

В основе линеаризации нелинейных уравнений лежит предположение о том, что в исследуемом динамическом процессе переменные изменяются так, что их отклонения от установившихся значений, т.е. величины , остаются все время достаточно малыми. Это допущение является справедливым в силу принципа работы замкнутой САУ.

Разложим функции Fив уравнении (2.1) в ряд Тейлора по степеням указанных выше малых отклонений, рассматривая все производные тоже как самостоятельные переменные. Тогда уравнение (2.1) примет вид:

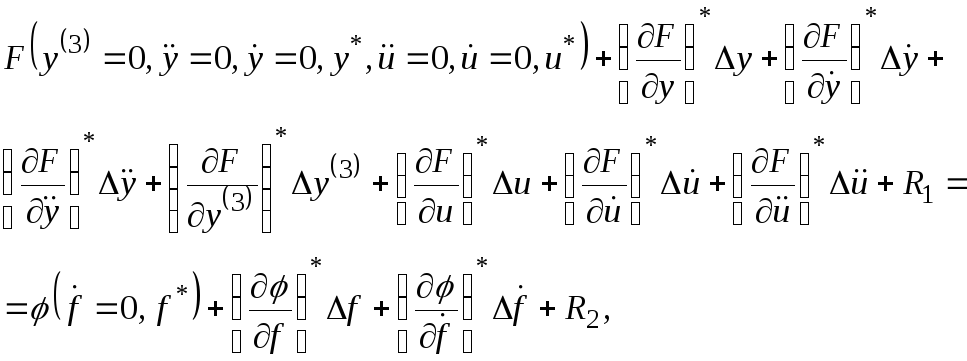(2.4)

где , например, означает частную производную, вычисленную при значениях переменных, соответствующих установившемуся режиму;R₁– остаток ряда Тейлора для функцииF, содержащий члены выше 1-го порядка малости;R₂– остаток ряда Тейлора для функции, содержащий члены выше 1-го порядка малости.

Вычтя из уравнения (2.4) уравнение установившегося состояния (2.2) и отбросив члены высшего порядка малости R₁иR₂ , получим искомое линеаризованное уравнение динамики исследуемой системы в виде

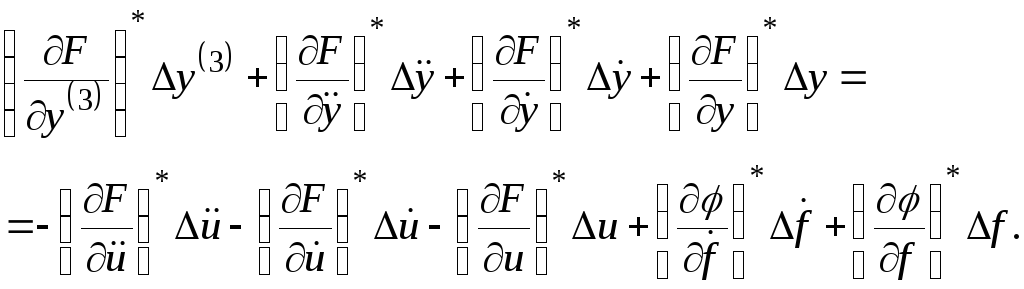(2.5)

Уравнение (2.5) называется дифференциальным уравнением системы (или ее отдельного звена) в отклонениях. Это уравнение записывают так, чтобы выходная величина и ее производные находились в левой части уравнения, а входная величина и все остальные члены – в правой части. Для коэффициентов уравнения (2.5) применим более простые обозначения

(2.6)

где n,m,r– порядки старших производных выходной величиныy, входной величиныuи возмущенияfсоответственно. С учетом обозначений (2.6) уравнение (2.5) примет вид:

+++=++++. (2.7)

Часто для упрощения записи знак вариации в уравнении (2.7) опускают, не забывая при этом, что все переменные есть отклонения исходных величин от их установившихся значений. В общем случае уравнение (2.7) может быть записано в виде:

++…++=++…++++ ++…++. (2.8)

Для реальных систем обычно выполняется соотношение n>m,n>r.