10.3. Составление разностных уравнений импульсной системы

Запишем разностные уравнения разомкнутой импульсной системы, структурная схема которой показана на рис.10.1. Подобные системы называют импульсными фильтрами. Непрерывная часть и формирующее устройство образуют приведенную непрерывную часть (ПНЧ) импульсного фильтра, на вход которого подаются мгновенные импульсы (рис.10.2).

Рассмотрим один из способов получения разностных уравнений, основанный на решении дифференциальных уравнений непрерывной части фильтра в интервале iTt<(i+1)T. При этом значения выходной величиныy(i),y(i-1),… рассматриваются как начальные условия. При подстановке в найденное решениеy(), =t-iTпредельного значения =Тполучим дискретуy(i+1).

Пример.Записать разностное уравнение разомкнутого дальномера с одним интегратором, широко применяемого в радиолокационных станциях. Передаточная функция интегратораW₀(s)=k/s.

Решение. Разностное уравнение формирователя, устанавливающее связь между последовательностями сигналов u^*(t)=u(i) иu_^*(t), имеет вид:

u_^*(i)= u(i). (10.22)

Дифференциальное уравнение непрерывной части определяет зависимость выходного сигнала y(t) от сигнала на входе НЧu_^*(t):

(10.23)

Найдем решение уравнения (10.23) на интервале времени iT t(i+1)T, когдаu_^*(t)= u(i)1(t-iT).

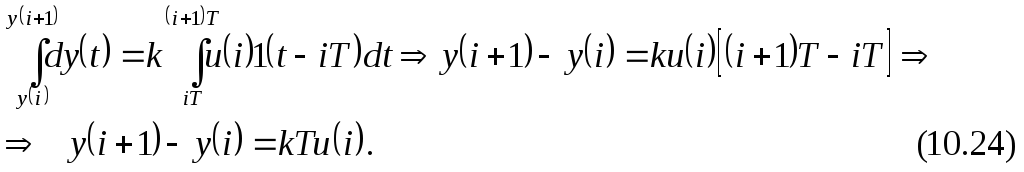
Уравнение (10.24) и есть искомое разностное уравнение, которое можно записать также в форме (10.6):

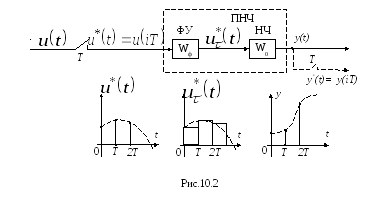
(10.25)

Тема 11.Дискретное преобразование Лапласа и передаточные функции импульсных систем

11.1. Понятие о z-преобразовании

Для последовательностей мгновенных импульсов вида (9.4)

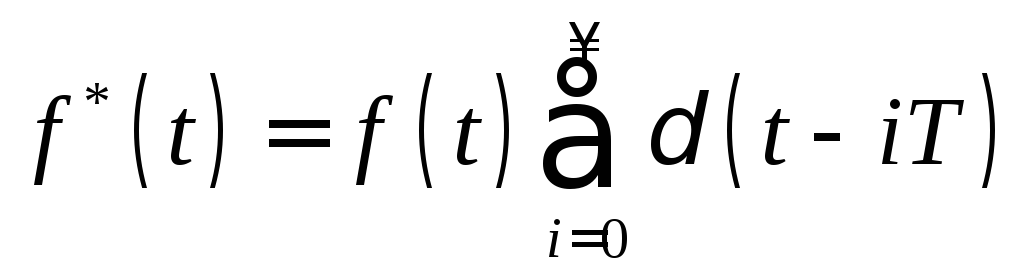
может быть введено понятие дискретного преобразования Лапласа, определяемое формулой

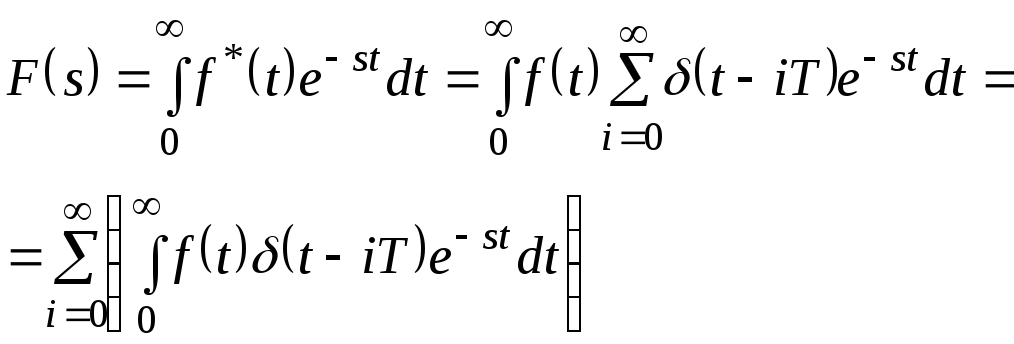(11.1)

Определяя каждый интеграл в выражении (11.1) по аналогии с (9.9), приведём (11.1) к виду:

F(s)=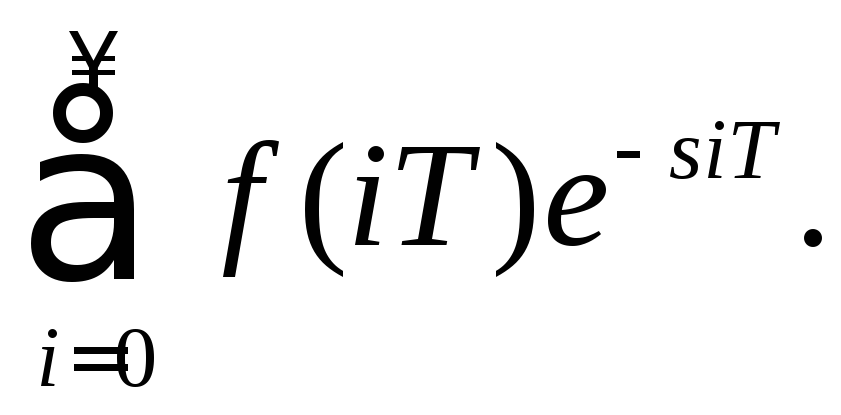(11.2)

Введём новую комплексную переменную, аналогичную переменной (10.12):

(11.3)

Тогда выражение(11.2) принимает вид:

(11.4)

Функцию F(z) называютz-преобразованием сигналаf(t). Часто формулу(11.4) записывают, опуская обозначение периода дискретности как аргумента функцииf(t):

(11.5)

Формулу преобразования (11.5) можно записать в символической форме:

F(z)=Z[f(i)] илиF(z)=Z[f(t)],t=iT,i=0,1,2,… (11.6)

Пример. Определитьz-преобразование сигналаx(t)=1(t).

Решение. В соответствии с (11.5)

Видно, что X(z) есть сумма бесконечной геометрической прогрессии, первый член которойа₀=1, а знаменатель прогрессииq=z^-1. Сумма (n+1) членов прогрессии равна

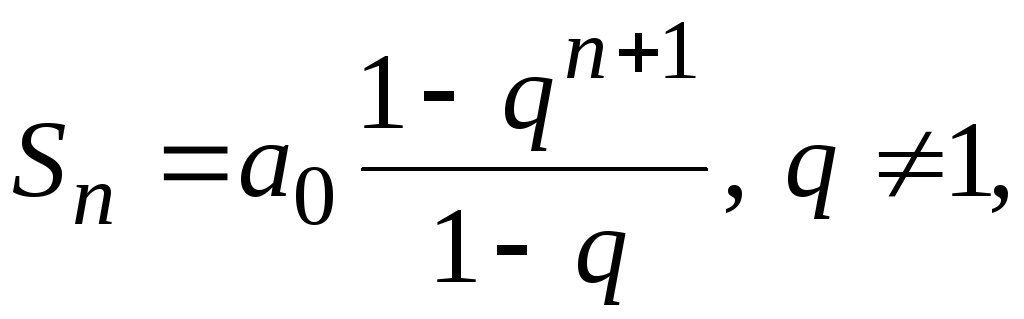
следовательно,

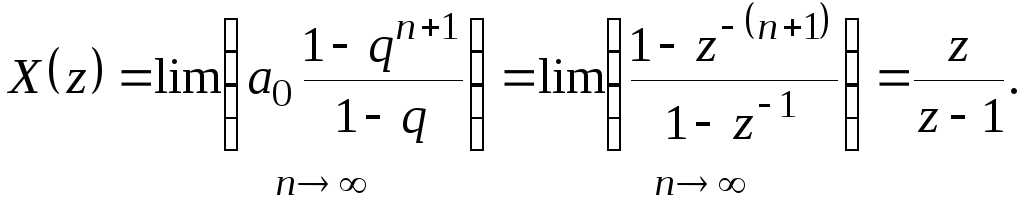(11.7)

Рассмотрим некоторые правила и теоремы применительно к z-преобразованию.

1.Свойство линейности.

Изображение линейной комбинации последовательностей равно той же линейной комбинации их изображений.

Пусть f(i)=. (11.8)

Тогда для изображения можно записать

F(z)=. (11.9)

2.Теорема запаздывания и упреждения.

Рассмотрим последовательность f(i-m), сдвинутую вправо (запаздывающую) на целое число тактовm. Тогда из формул (11.5), (11.6) следует

Z[f(i-m)]=f(i-m)z ^-i. (11.10)

Обозначим в формуле (11.10) r=i-m.Тогдаi=r+m, приi=0r=-m, при, а формула (11.10) примет вид:

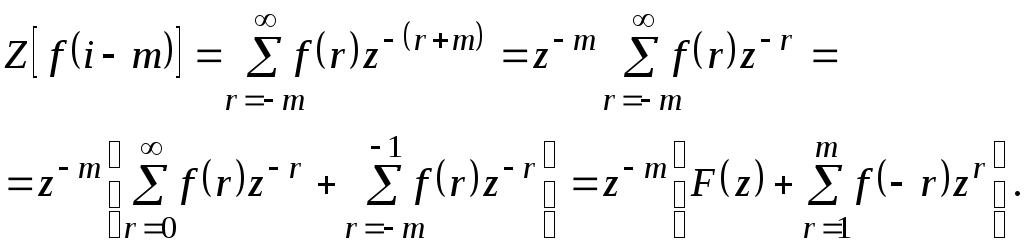(11.11)

Здесь F(z)=Z[f(i)]. Если исходная последовательностьf(i) равна нулю при отрицательных значениях аргумента (нулевые начальные условия), то формула(11.11) упрощается:

Z[f(i-m)]=z ^-mF(z). (11.12)

Если сдвиг происходит влево (упреждение) и рассматривается последовательность f(i+m), гдеm-целое положительное число, то аналогично случаю запаздывания можно показать, что

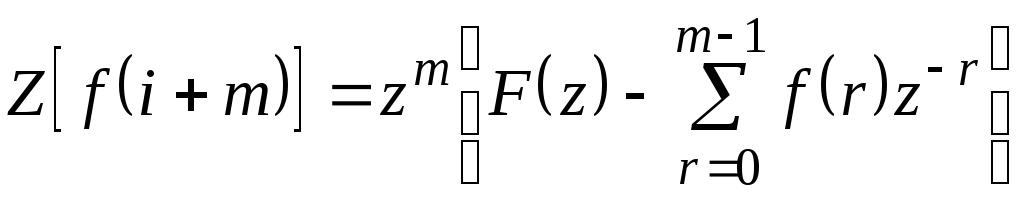(11.13)

Второе слагаемое в правой части(11.13) обращается в нуль, если f(i)=0 приi=0,1,...,m-1.

3.Сумма ординат последовательности.

Формула z-преобразования (11.5) при(что соответствует условию) даёт сумму ординат последовательностиf(i):

F(1)=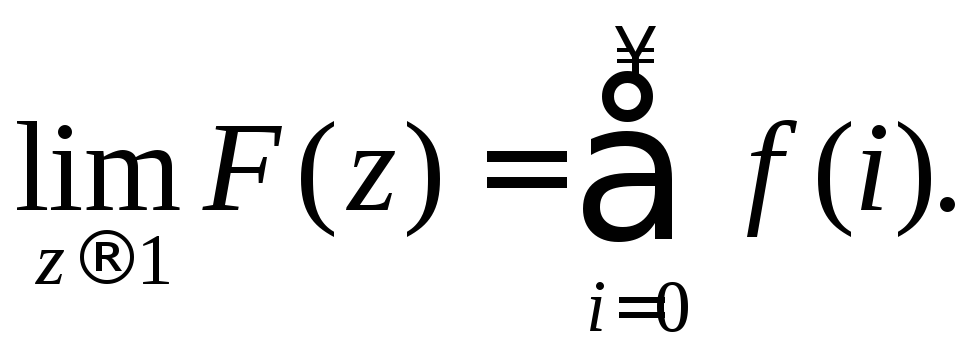(11.14)

4. Конечное значение последовательности.

Составим первую прямую разность последовательности f(i) и на основании (11.9) найдём её изображение

Z[∆f(i)]=Z[f(i+1)-f(i)]=Z[f(i+1)]-Z[f(i)]=z[F(z)-f(0)]-F(z)=

=(z-1)F(z)-zf(0).

Далее на основании (11.14) найдём сумму ординат ∆f(i):

(11.15)

Кроме того, можно записать, что сумма ординат ∆f(i) есть разность между значениемf(i) приiи начальной ординатойf(0):

(11.16)

Значение f(i) приiесть конечное значение последовательности. Из двух последних выражений следует:

(11.17)

Пример. Определить конечное значение выходной величиныy(i) импульсной системы, описываемой разностным уравнением (10.9), при начальных условияхy(-1)=y(-2)=0 и единичной входной последовательностиu(t)=1(t), т.е.u(0)=u(1)=...=1,u(i)=0 приi<0.

Решение. Применим к разностному уравнению (10.9) z‑преобразование и на основании свойства линейности получим выражение

Z[y(i)] - 0,27 Z[y(i-1)] + 0,135 Z[y(i-2)] = 0,865 Z[u(i-1)], (11.18)

где Z[y(i)]=Y(z);

Z[y(i-1)]=z ^-1[Y(z)+y(-1)z]=z ^-1Y(z);

Z[y(i-2)]=z ^-2[Y(z)+y(-1)z+y(-2)z²]=z ^-2Y(z);

Z[u(i-1)]=z ^-1[U(z)+u(-1)z]=z ^-1U(z) .

В соответствии с (11.7) изображение единичной последовательности

Z[u(i)]=U(z)=.

Из уравнения (11.18) определим изображение выходной величины:

Y(z)=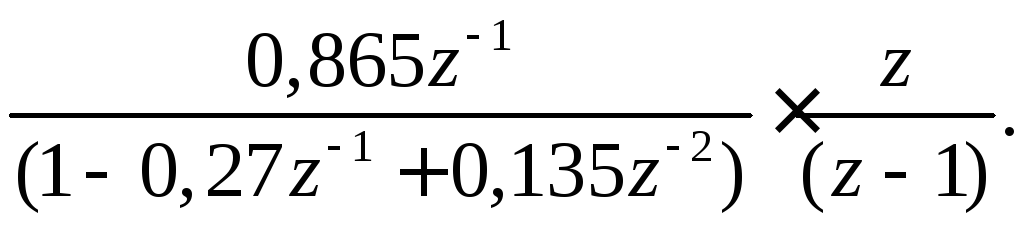

Конечное (установившееся) значение выходной величины найдём по формуле (11.17):

.
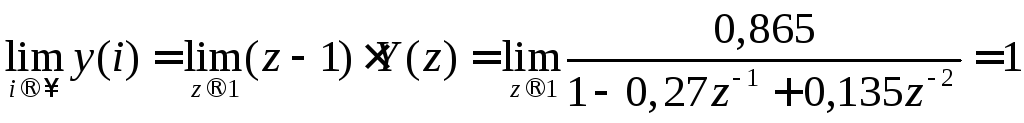