11.2. Определение передаточных функций импульсной системы.

Найдем передаточную функцию разомкнутой импульсной системы, структурная схема которой представлена на рис. 10.2.

Передаточная функция импульсного фильтра легко определяется, если известно разностное уравнение (10.5) или (10.6), которое с помощью z-преобразования при нулевых начальных условиях можно привести к виду

C(z)Y(z)=B(z)U(z), (11.19)

где C(z)=c₀zⁿ+c₁z^n-1+…+c_n;B(z)=b₀z^m+b₁z^m-1+…+b_m;

Y(z)=Z[y(i)];U(z)=Z[u(i)].

Дискретная передаточная функция W(z) есть отношение двух изображений (выходной и входной величин) при нулевых начальных условиях:

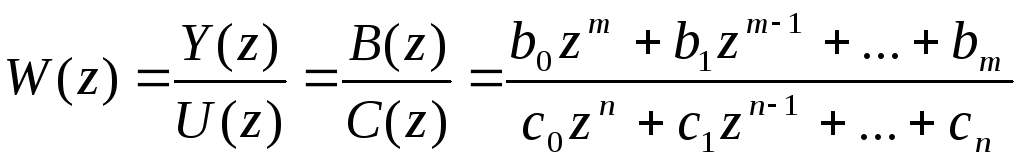(11.20)

Дискретная передаточная функция играет такую же роль в импульсных и цифровых системах, как и обычная передаточная функция в непрерывных системах.

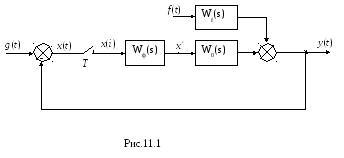
Рассмотрим теперь замкнутую импульсную систему, структурная схема которой показана на рис.11.1, где W_f(s) – передаточная функция разомкнутой системы по возмущению.

Основу этой системы составляет схема, изображенная на рис.10.2, при x(i) =u(i). Тогда изображение управляемой величиныy(t) приf(t)=0

Y(z) =W(z)X(z), (11.21)

где W(z) - передаточная функция разомкнутой системы.

Так как приведенная непрерывная часть системы реагирует на значение ошибки системы х(t) =g(t) –y(t) только в дискретные моментыt=iT, то замыкающее уравнение может быть записано как разностное

х(i) =g(i) –y(i)

или в изображениях

X(z) =G(z) –Y(z). (11.22)

Из уравнений (11.21), (11.22) получим:

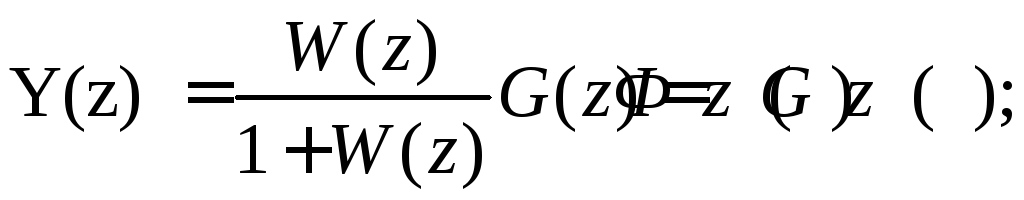(11.23)

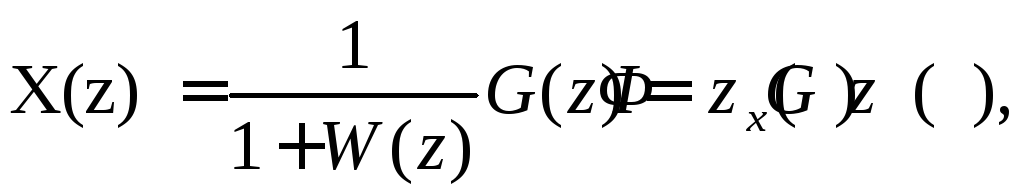(11.24)

гдеФ(z)=W(z)/(1+W(z)) – передаточная функция замкнутой системы,Ф_x(z)=1/(1+W(z)) – передаточная функция замкнутой системы по ошибке.

Пример 1.Определить дискретную передаточную функцию разомкнутого дальномера с одним интегратором (см.пример из раздела 10.3).

Решение. Разностное уравнение данного импульсного фильтра получено в виде

Выполним z‑преобразование разностного уравнения:

(z-1)Y(z)=kTU(z).

Далее найдем дискретную передаточную функцию по формуле (11.20):

Пример 2.Определить дискретные передаточные функцииФ(z),Ф_x(z) замкнутого дальномера с одним интегратором (см. пример 1 данного раздела).

Решение. На основании формул (11.20), (11.23) и (11.24) получим:

Тема 12. Устойчивость и оценка качестваимпульсных систем

12.1. Исследование устойчивости по корням характеристического уравнения

В разделе 7.1 было показано, что непрерывная система устойчива, если все корни s_v(v=1,2,…,n) ее характеристического уравнения лежат в левой полуплоскости (рис.12.1a). При исследовании импульсных систем вместоsиспользуется новая переменнаяz=е^Ts . В теории функций комплексного переменного преобразование, в процессе которого одна переменная заменяется некоторой функцией от новой переменной, а одна область комплексной плоскости отображается в другую, называется конформным преобразованием. Конформное преобразованиеz=e^Tsотображает левую полуплоскость плоскостиsв область, ограниченную окружностью единичного радиуса на плоскостиz(рис. 12.1 б). При этом мнимая ось плоскостиs отображается в саму окружность.

Действительно, пусть s_1,2 =. Тогда

При этом . Для значений(что соответствует корнямs_1,2, лежащим в левой полуплоскости плоскостиs), что соответствует корнямz_1,2, лежащим внутри круга единичного радиуса плоскостиz. Если, т.е. еслиs_1,2располагаются на мнимой оси плоскостиs, то корниz_1,2 попадают на окружность единичного радиуса плоскостиz.

Таким образом, импульсная система устойчива, если все корни ее характеристического уравнения лежат внутри круга единичного радиуса, т.е. если,, что совпадает с условием (10.17).Если хотя бы один корень лежит вне круга единичного радиуса, то система неустойчива.

Окружность единичного радиуса представляет собой границу устойчивости для импульсной системы.

Система находится на апериодической границе устойчивости, если в ее характеристическом уравнении

a₀zⁿ+a₁z^n-1+…+a_n=0 (12.1)

имеется корень z_v=1, а остальные корни располагаются внутри круга единичного радиуса (рис.12.1 в). В этом случае переходная составляющая решения разностного уравнения (10.16) с течением времени стремится к значениюC_v(z_v)ⁱ=C_v.

Если в характеристическом уравнении имеется пара комплексных сопряженных корней, расположенных на окружности единичного радиуса (рис.12.1 г), т.е. таких, что , то имеет место колебательная граница устойчивости. В этом случае с течением времени в системе устанавливаются незатухающие колебания. Например, если бы в решении разностного уравнения (10.8)модуль комплексных сопряженных корнейА был равен 1, то это привело бы к незатухающим колебаниям с частотой. Вещественная часть указанных корней Re(z_v,v+1) может быть положительной, как на рис.12.1 г, отрицательной или нулевой.

Типичной для импульсных систем является так называемая граница устойчивости третьего типа, которой соответствует наличие в характеристическом уравнении корня z_v= -1 (рис. 12.1 д). В этом случае в системе с течением времени устанавливаются незатухающие периодические колебания с периодом 2Т, так как составляющая решения (10.16)при измененииiпоследовательно принимает значениеи ‑.

Для оценки устойчивости и качества импульсных систем используются передаточные функции разомкнутой системы W(z) и передаточные функции замкнутой системыФ(z) илиФ_х(z). В соответствии с выражениями (11.23) или (11.24) характеристическое уравнение замкнутой системы (12.1) может быть получено следующим образом:

1+W(z)=0;B(z)+C(z)=0, (12.2)

где B(z) иC(z) – полиномы числителя и знаменателя передаточной функцииW(z).