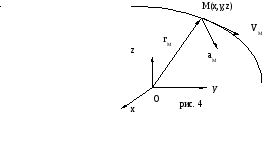
§ 2. Координатный способ задания движения точки.

Координатный способ легко может быть получен из векторного. Точку отсчёта

(полюс) О примем за начало координат, например, прямоугольных осей XYZ (рис.4).

Тогда положение точки М в пространстве

можно задать координатами X_M;Y_M;Z_M, а

введённые в векторном способе векторы

могут быть записаны:

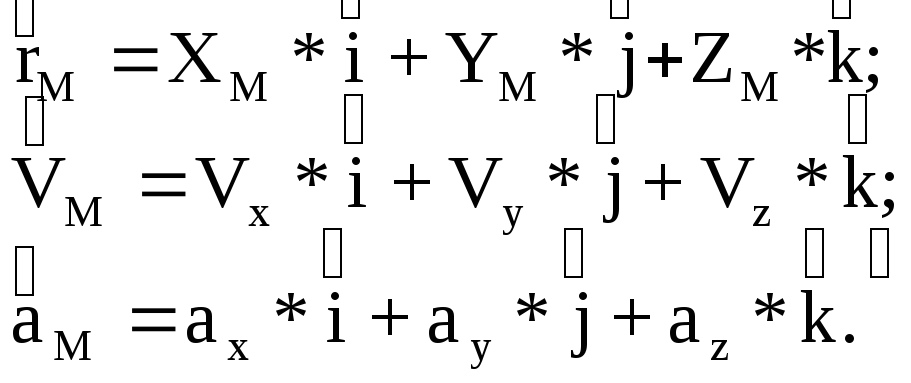
Как видим, в координатном способе векторы

однозначно определяются их тремя

проекциями на оси координат.

Уравнения X_M=f(t); Y_M=f(t); Z_M=f(t)

называются уравнениями движения точки в координатной форме. Математически их можно рассматривать как уравнения траектории точки в параметрической форме. Исключив параметр t, получим уравнение траектории в координатной форме: Z=f(X,Y).

По определению:

Следовательно:

и

Аналогично:

Следовательно:

Пример: Движение точки в плоскости XY задано уравнениями:

Определить форму траектории и получить формулы для вычисления скорости и ускорения.

Решение:

Исключим параметр t из уравнений движения: сложим

и

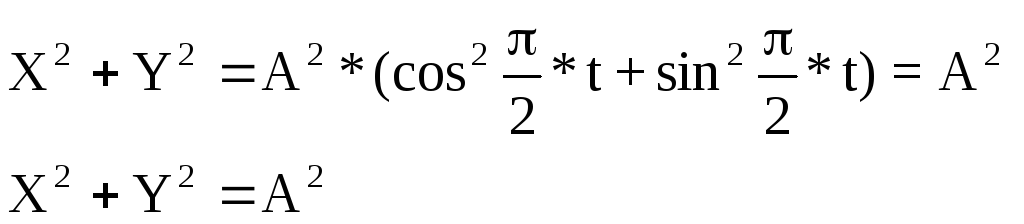
Форма траектории - окружность радиуса А.

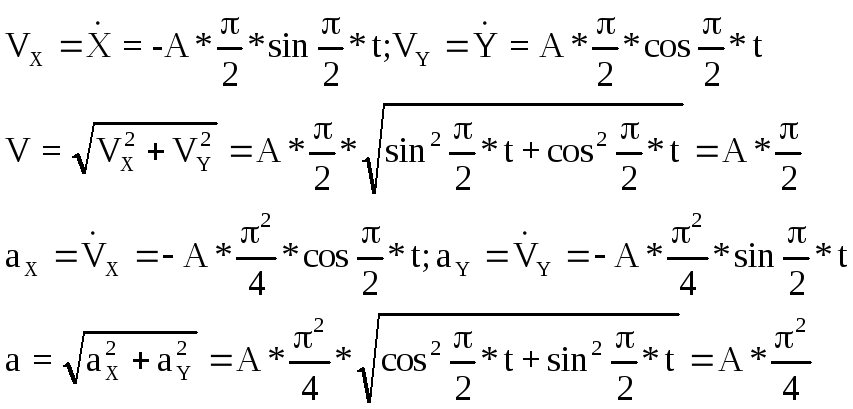
§ 3 Естественный метод задания движения точки.

В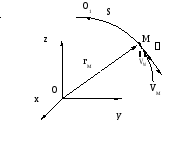стречаются задачи, когда траектория точки задана её условиями. В этом случае положение точки в пространстве может определяться криволинейной (дуговой)координатой S, отмеряемой от некоторой начальной точки отсчёта О до исследуемой точки М вдоль траектории (рис.5). Уравнение вида S=f(t) называется уравнением движения точки при естественном способе задания её движения. Рассмотрим теперь методы определения скорости и ускорения точки при естественном способе задания движения:

1)По определению

Представим: , где

единичный вектор,

касательный к траектории в точке М

и направленный в строну увеличения

дуговой координаты.

- алгебраическая величина (модуль)

скорости; может принимать как положительные так и отрицательные значения.

Таким образом:

По определению:

Замечаем, что при таком представлении вектор ускорения раскладывается на две составляющие.

Рассмотрим их геометрический смысл.

Видно, что первое слагаемое проектируется на касательную к траектории и называется касательным ускорением.

Покажем, что второе слагаемое проектируется на нормаль к траектории и поэтому называется нормальным ускорением.

Представим:

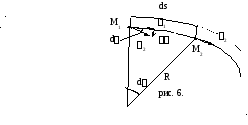
Геометрический смысл производной

можно уяснить из рис.6 .

Определим модуль вектора :

dS=R*dЄ

dЄ=dЄ()

Таким образом:

Определим направление вектора .

В заштрихованном равнобедренном треугольнике сумма углов

dЄ+2*,откуда

Є

При dsЄ

Следовательно, в пределе , таким образом векторнормален к касательной и направлен к центру кривизны траектории. Окончательно:

В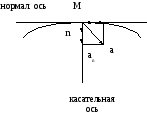озвратимся теперь к полному выражению для ускорения точки при естественном способе задания её движения

Касательная составляющая полного ускорения

характеризует изменение скорости по величине

(при V=const ).

Нормальная составляющая полного ускорения

характеризует изменение вектора скорости по

направлению (при движении по прямой R=и)

В общем случае ;

При рассмотрении естественного способа задания движения точки введены понятия касательной и нормальной осей к траектории в точке М. Эти оси называются естественными осями координат. Их особенностью является движение вместе с точкой М по траектории, они поворачиваются вместе с изгибами траектории (рис.8).

Рассмотрим теперь один из

способов установления аналитической

связи между проекциями ускорения точки

в естественных и прямоугольных осях

координат.

Имеем выражение для модуля

с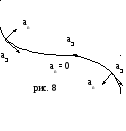корости точки

Продифференцируем это выражение

по времени:

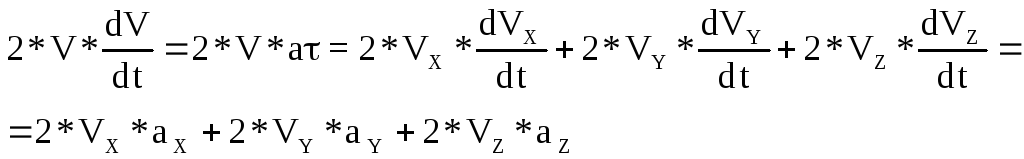
Таким образом и

Пример: Точка движется по окружности радиуса R=1м согласно уравнению S=¶ * t,м. Определить скорость, касательное, нормальное и полное ускорения точки при t=1с.

Решение:

[м/c]

[м/с²]

[м/c²]

[м/c²]