§ 6. Решение задач на равновесие тела под действием пространственной системы сил.

Уравнения равновесия (1-6) пространственной системы сил получены в § е3.

Принцип решения таких задач остаётся тем же, что и для плоской системы сил:

1.Вводят пространственную систему координат XYZ.

2.Освобождаются от связей, заменяя их действие силами и моментами реакций.

3.Распределённые нагрузки заменяют условно сосредоточенными.

4.Составляют и решают систему уравнений равновесия относительно неизвестных сил и моментов.

Некоторые трудности могут возникнуть с вычислением моментов относительно координатных осей. Выше указывалось, что для этого необходимо силу спроектировать на плоскость, перпендикулярную оси и умножить эту проекцию на кратчайшее расстояние до оси.

В тех случаях, когда при вычислении момента силы затруднено вычисление расстояния от проекции силы до соответствующей оси, рекомендуется разложить силу на две взаимно перпендикулярные составляющие, одна из которых параллельна какой-нибудь координатной оси, а затем воспользоваться теоремой Вариньона.

Кроме того, осевые моменты можно вычислять аналитически по формулам.

Пример: Для конструкции, изображённой на рисунке (рис.28) составить уравнения равновесия с целью определения силы F, необходимой для удержания в равновесии силы Р и опорных реакций в подшипниках А и В.

Решение:

1.Вводим систему координат XYZ с

началом в точке А. 2.Освобождаемся

о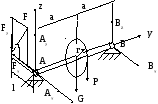т связей в цилиндрических подшипниках

А и В в виде искомых реакций A_X; A_Z; B_X; B_Z..

Для удобства вычисления осевых моментов от

наклонной силы F разложим её напроекции:

F_x = -F*cos ; F_x =-F*sin .

Рис.28.

4.Составляем уравнения равновесия:

F_x =-F * cos +A_x + B_x = 0 (1)

F_y = 0 (2)

F_z =-F * sin +A_z - G - P + B_z = 0 (3 )

M_x = - G * a - P * a + B_z * 2 * a = 0 (4)

M_y = - F * sin  * l + P * r = 0 (5)

M_z = - B_x * a = 0 (6)

Тема 4. Параллельные силы. Центр тяжести. Силы трения.

§ 1. Система параллельных сил.

Параллельными называют силы, линии действия которых параллельны.

Различают плоские и пространственные системы параллельных сил. Частным случаем двух параллельных сил является пара сил. Решение задач с участием параллельных сил имеет ряд особенностей. Рассмотрим некоторые из них.

а) Сложение двух параллельных сил.

Две параллельные силы (кроме пары сил) можно заменить их равнодействующей.

Рассмотрим это на примере двух сил, направленных в одну сторону.

Пусть на тело действуют

две параллельные силы F₁

и F₂, приложенные

соответственно в точках А

и В.(рис.29). Приложим в

точках А и В тела две равные

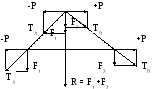по величине противоположно

направленные силы Р и -Р.

Рис.29.

Полученная система из 4-х сил эквивалентна исходной. Сложим векторно силы в точках А и В и полученные силы Т_А=F₁+P и Т_В=F₂+P переместим в точку их пересечения О. Далее в точке О разложим силы Т_А и Т_В на составляющие Р и -Р, F₁ и F₂. Отбросив силы Р и -Р, получим две силы F₁ и F₂, исходящие из точки О и лежащие на одной линии действия, пересекающей прямую АВ в точке С.

Очевидно арифметическая сумма сил R=F₁+F₂,приложенная в точке С и полученная путём эквивалентных переходов, заменяет действие двух параллельных сил F₁ и F₂,приложенных в точках А и В и является их равнодействующей. Рассматриваяподобие силовых треугольников в точке О и геометрических треугольников АОС и ВОС, легко убедиться, что точка С делит линию АВ на участки, обратно пропорциональные модулям сил F₁и F₂.Действительно

и или Р*ОС=АС*F₁=BC*F₂.

Получили правило:

Равнодействующая двух параллельных сил, направленных в одну сторону, равна их арифметической сумме и направлена в ту же сторону. Линия действия равнодействующей делит расстояние между линиями действия сил на отрезки, обратно пропорциональные модулям сил.

Без доказательства сформулируем правило сложения сил, направленных в разные стороны.

Рис.30.

Равнодействующая двух параллельных сил,

направленных в разные стороны, равна их

арифметической разности и направлена в

сторону большей силы. Линия действия её

через точку С, которая находится за пределами

отрезка АВ со стороны большей силы; при этом

сохраняется условие:

AC*F₁=BC*F₂ .

Рис.31.

б) Центр параллельных сил.

Пусть задана произвольная система

параллельных сил, направленных в

одну сторону. Производя последова-

тельное попарное сложение по правилу,

полученному в пункте (а), приведём их

к одной равнодействующей силе,

р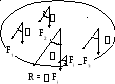авной их арифметической сумме и

направленной в ту же сторону.

рис. 31.

Повернём все параллельные силы на одинаковый угол . Очевидно при этом на тот же угол повернётся и их равнодействующая, не изменившись при этом по величине (рис.31).

Точка С, вокруг которой поворачивается линия действия равнодействующей системы параллельных сил при их одновременном повороте, называется центром параллельных сил.

Получим формулы для вычисления координат центра параллельных сил.

Пусть система параллельных сил

Р₁;P₂...P_i...Р_n задана в координатах

XYZ, при этом ось Z параллельна

силам и их равнодействующей.

Силы заданы их модулями и координатами

точек приложения. При таком выборе

осей координат для всех сил

P_{i x}=P_{i y}=0 R _{i x}=R _{i y}=0

P_{i z}=-P_i R_z=-R .

Рис.32.

Вычислим моменты всех сил системы относительно координатных осей с помощью аналитических выражений

M_{1 y}=Z₁*P_{1 x} - X₁*P_{1 z}=P₁*X₁

. . . . . . . . . . . . . . . . . . . . . . .

M_{i y}=Z _i*P_{i y} - X _i *P_{i z}=P_i*X _i

. . . . . . . . . . . . . . . . . . . . . . .

M_{n y}=Z_n*P_{n y} - X_n*P_{n z}=P_n*X_n

------------------------------------

M_{R y}=Z_c*R_y - X _c*R _z=R*X _c

По теореме Вариньона M_{R y} =M_{i y}, следовательно

R*X _c=P_i *X _i

Таким образом X _c=

Записывая выражение для моментов относительно оси X ,получим:

Y_c=

Для нахождения координаты Z _c повернём все силы на 90⁰ таким образом,чтобы все силы и их равнодействующая оказались параллельными, например оси X . Путём аналогичных рассуждений получим Z _c=