§ 3. Уравнения равновесия произвольной системы сил.

Запишем полученные в предыдущем § е векторные условия равновесия произвольной системы сил:

Но

Замечаем, что условия равновесия произвольной системы сил в координатной форме запишутся:

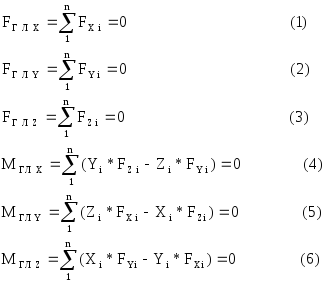
Система уравнений (1 - 6) называется уравнениями равновесия произвольной системы сил в координатной форме. Эти уравнения содержат как задаваемые силы и моменты, так и силы и моменты от сил реакции связей. В задачах статики часть этих сил и моментов не задана и подлежит определению. Естественно, что число неизвестных сил и моментов не должно превышать числа уравнений равновесия. В противном случае говорят, что задача становится статически неопределимой.

§ 4. Теорема Вариньона.

При решении некоторых задач статики удобно пользоваться теоремой Вариньона.

Теорема: Если некоторая система сил в точке О приводится к равнодействующей (2-й случай приведения), то момент этой равнодействующей относительно другой точки О₁ равен сумме моментов сил системы относительно точки О₁.

Действительно:

Для силы системы F_i справедливы

с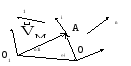оотношения:

_o1i=_oi_i

_i=_oi_i

Так как заданная система

сил в точке О сводится

к равнодействующей, то Представив,найдём сумму моментов сил системы относительно точки О₁:

Теорема Вариньона позволяет упростить задачу вычисления момента силы F относительно полюса О в тех случаях, когда определение плеча силы затруднительно. Например задан полюс О и вектор силы F с точкой приложения А, координаты которой X_A и Y_A (рис.20,а).

_y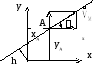

Рис.20.

Представив силу F как равнодействующую двух взаимно перпендикулярных сил

вычислим момент силы F относительно полюса О:

M_O(F)=F*h=-F_x*Y_A+F_y*X_A=-F*cos*Y_A+F*sin*X_A.

§ 5.Уравнения равновесия системы сил в некоторых частных случаях.

а) Уравнения равновесия сходящейся системы сил.

Определение: Система сил называется сходящейся, если линии действия всех сил пересекаются (сходятся) в одной точке. Учитывая, что вектор силы есть скользящий вектор, все силы можно перенести в точку пересечения их линий действия и получить пучок сил.

Из рис.21 очевидно, что сходящаяся

система сил в точке О приводится к

равнодействующей

Рис.21.

Сумма моментов этих сил относительно точки их пересечения О тождественно равна нулю.

Следовательно, векторным условием равновесия сходящейся системы сил является

В проекциях на прямоугольные оси координат это условие перепишется в виде трёх уравнений:

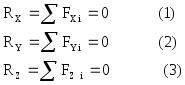
Уравнения (1-3) называются уравнениями равновесия сходящейся системы сил в координатной форме. Заметим, что если сходящаяся система сил лежит в плоскости XY, то уравнение (3) превращается в тождество.

Отметим также, что уравнение (1-3) легко получаются из общих уравнений равновесия (1-6) для произвольной системы сил (см. § 3), если учесть особенности сходящихся сил. Исходя из сказанного, легко наметить план решения задач на равновесие сходящейся системы сил:

1.Выбрать систему координат XYZ .

2.Освободиться от связей, заменив их силами реакции.

3.Найти проекции всех сил на координатные оси.

4.Составить и решить уравнения равновесия относительно неизвестных сил.

Примечание: В ряде случаев исследование равновесия сходящихся сил удобнее производить геометрическим способом, учитывая, что у равновесной системы сходящихся сил силовой многоугольник замкнут.

Рис.22.

Пример:

Определить усилия в шарнирных стержнях АС и ВС от действия вертикальной нагрузки P.

Обозначим усилия в стержнях S_A и S_B, приняв их растянутыми, составим уравнения равновесия

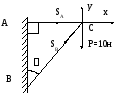
Решая систему уравнений в цифрах, получим:

S_B=-11,6 Н(сжат) S_A=5,8 Н(растянут).

Рис. 23.

б) Уравнения равновесия плоской системы сил. Система сил называется плоской, если линии действия всех сил располагаются в одной плоскости

Уравнения равновесия плоской системы

сил могут быть получены из уравнений

равновесия произвольной системы сил

(см.§ 3), если учесть аналитические

условия, определяющие особенности

плоской системы сил, например,

расположенной в плоскости XY:

(рис.24 )

Так для всех сил плоской системы, проекции их на ось Z равны нулю (F_{Z i}=0). Кроме того, нулю равны и Z-е координаты всех точек приложения сил. Таким образом, будем иметь:

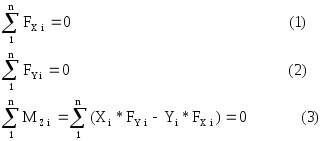
Система уравнений(1-3)называется уравнениями равновесия плоской системы сил. Отметим, что при составлении этих уравнений равновесия выбор координатных осей произволен. Однако решение задачи значительно упростится, если назначенные оси координат окажутся перпендикулярными или параллельными большинству сил системы, а начало координат лежит на пересечении возможно большего числа линий действия неизвестных сил.

При решении задач на исследование равновесия тел, наряду с сосредоточенными силами, приложенными в одной точке, могут действовать и распределённые нагрузки. Примерами распределённых нагрузок могут служить массовые силы, аэродинамические силы и др.

Распределённые нагрузки на схемах задаются:

- эпюрой распределения нагрузки;

- интенсивностью распределённой нагрузки;

- протяжённостью распределённой нагрузки(рис.25)

а)Прямоугольная эпюра б)Треугольная эпюра

q, н/м-интенсивность q_max., н/м - максимальная интенсивность

а, м-протяжённость а, м - протяжённость

Q=q*a, Q - условная сосредо- Q=0.5*q_max*a, Q - условная сосредеточен-

точенная сила ная сила

Рис.25.

Перед составлением уравнений равновесия следует распределённые нагрузки заменять условно сосредоточенными силами. Величина условно сосредоточенной силы пропорциональна площади эпюры, а линия её действия проходит через центр тяжести эпюры.

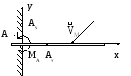
В этом § е уместно рассмотреть ещё один тип связей, не вошедший в таблицу 1 (см. § 3). Этот тип связей называется защемлённая или жёсткая заделка, схематически изображённая на рис. 26.

Жёсткая заделка А в плоской задаче

не позволяет задаваемым силам F

перемещать тело в направлении

координатных осей X и Y и не

позволяет поворачивать его

относительно точки А(оси Z).

Рис.26.

Следовательно, в жёсткой заделке возникают две составляющие силы реакции

A_X и A_Y, а также момент реакции M_A (M_Z).

Исходя из всего сказанного, можно наметить план решения задач на равновесие плоской системы сил:

1.Выбрать систему координат XY.

2.Освободиться от связей, заменив их силами и моментами реакций.

3.Заменить распределённые нагрузки условно сосредоточенными силами.

4.Составить и решить уравнения равновесия относительно неизвестных сил и моментов.

Пример: Однородная консольная балка длиной l=2 м и погонной массовой нагрузкой q=10кг/м нагружена сосредоточенной силой F=20Н и парой сил

M=10Н*м.Определить опорные реакции балки в точке защемления А.

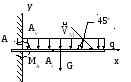Решение.

1.Вводим оси координат XY c

началом в точке А.

2.Освобождаемся от связи в виде

искомых реакций A_X;A_Y;M_A.

3.Заменяем массовую погонную

нагрузку балки q условно

сосредоточенной силой G

(силой тяжести), приложить её в

центре балки

Рис.27.

G=q * g * l=10*9,8*2=19,6 Н.

4.Составляем уравнения равновесия:

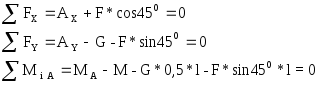
или в цифрах: Решаем:

А_X+20*0,7=0; A_X=-14 H

А_Y-19,6-20*0,7=0; A_Y=33,6Н

M_A-10-19,6*1-20*0,7*2=0 М_А=57,6 Нм.