
- •Теоретическая механика
- •§ 2 Аксиомы статики
- •5. Аксиома равенства действия и противодействия:
- •§ 3 Связи. Силы реакции связей. Аксиома связей
- •Тема 2. Момент силы пара сил.
- •§ 1. Момент силы относительно точки и оси.
- •§ 2.Пара сил и её свойства.
- •Тема 3. Произвольная система сил.
- •§ 1.Теорема о параллельном переносе силы.
- •§ 2.Теорема о приведении произвольной системы сил к заданному центру(основная теорема статики).
- •§ 3. Уравнения равновесия произвольной системы сил.
- •§ 4. Теорема Вариньона.
- •§ 5.Уравнения равновесия системы сил в некоторых частных случаях.
- •§ 6. Решение задач на равновесие тела под действием пространственной системы сил.
- •Тема 4. Параллельные силы. Центр тяжести. Силы трения.
- •§ 1. Система параллельных сил.
- •§ 2. Центр тяжести твёрдого тела.
- •§ 3. Равновесие при наличии трения.
- •Раздел 2. Кинематика.
- •Тема 5. Кинематика точки.
- •§ 1. Векторный способ задания движения точки.
- •§ 2. Координатный способ задания движения точки.
- •§ 3 Естественный метод задания движения точки.
- •Тема 6. Простейшие движения тела.
- •§1. Поступательное движение твёрдого тела.
- •§ 2. Вращательное движение твёрдого тела.
- •Тема 7. Плоскопараллельное (плоское) движение тела.
- •Тема 8. Сложное движение точки.
- •§ 1. Понятия и определения.
- •§ 2. Теорема о скоростях точки при сложном движении.
- •§ 3. Теорема об ускорениях точки тела при сложном движении (теорема Кориолиса).
- •§ 4. Ускорение Кориолиса, его величина и направление; кинематический смысл.
- •Раздел 3. Динамика.
- •Тема 10. Дифференциальные уравнения движения материальной точки.
- •§ 1. Основные аксиомы динамики точки.
- •§ 2. Прямая и обратная задача динамики материальной точки.
- •§ 3. Дифференциальные уравнения движения материальной точки.
- •Тема 11. Колебания материальной точки.
- •§ 1. Введение
- •§ 2. Свободные колебания материальной точки (без учёта сил вязкости).
- •§ 3. Вынужденные колебания материальной точки.
- •Тема 12. Динамика относительного движения материальной точки.
- •Тема 13. Введение в динамику системы материальных точек.
- •§ 1. Основные свойства механической системы.
- •§ 2. Дифференциальное уравнение движения точек механической системы
- •§ 3. Теорема о движении центра масс механической системы.
- •§ 4. Понятие о моментах инерции твёрдого тела.
- •Тема 14. Общие теоремы динамики материальной точки и механической системы.
- •§ 1. Теорема об изменении количества движения.
- •§ 2. Теоремы об изменении момента количества движения.
- •§ 3. Теоремы об изменении кинетической энергии.
- •Тема 16. Элементарная теория удара .
- •§ 1. Общие теоремы теории удара.
- •§ 2. Удар шара о неподвижную поверхность.
- •§ 3. Прямой центральный удар двух тел( двух шаров).
- •§ 4. Удар по вращающемуся телу. Центр удара.
- •Тема 17. Метод кинетостатики.
- •§ 1. Метод кинетостатики для материальной точки.
- •§ 2. Метод кинетостатики для твёрдых тел и механической системы.
- •Тема 18. Элементы аналитической механики.
- •§ 1. Понятие об идеальных связях и обобщённых координатах механической системы.
- •§ 2. Принцип возможных (виртуальных) перемещений.
- •§ 3. Общее уравнение динамики.
- •§ 4. Уравнение Лагранжа II рода.
- •§ 5. Применение методов аналитической механики для анализа поведения механических систем в некоторых частных случаях.
§ 3. Теорема об ускорениях точки тела при сложном движении (теорема Кориолиса).
Используем полученное ранее выражение для скоростей в сложном движении
![]() .
.
В этом выражении
векторы V0
и
![]() определены
в абсолютной системе координат, а
определены
в абсолютной системе координат, а![]() и
и![]() - в подвижной(переносной).
- в подвижной(переносной).
Выражение для абсолютного ускорения получим дифференцированием этого выражения:
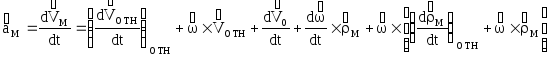
В полученном выражении:
![]() - относительное ускорение точки.
- относительное ускорение точки.
![]() - абсолютное
ускорение точки О.
- абсолютное
ускорение точки О.
![]() - вращательное
ускорение точки М подвижной системы
координат.
- вращательное
ускорение точки М подвижной системы
координат.
![]() - центростремительное
ускорение точки М подвижной системы
координат.
- центростремительное
ускорение точки М подвижной системы
координат.
Очевидно
![]() ,
,
где
![]() - переносное ускорение точки М.
- переносное ускорение точки М.
Оставшиеся слагаемые
![]() называют ускорением Кориолиса.
называют ускорением Кориолиса.
Окончательно:
![]() .
.
Доказана теорема: Абсолютное ускорение точки при сложном движении равно геометрической сумме относительного, переносного и кориолисова ускорений. Эта теорема носит название теоремы Кориолиса.
§ 4. Ускорение Кориолиса, его величина и направление; кинематический смысл.
При определении абсолютного ускорения точки в сложном движении наряду с относительным и переносным ускорениями в некоторых случаях возникает ускорение Кориолиса:
![]() .
.
Модуль этого ускорения определяется выражением
![]() .
.
Из этого выражения следует, что
у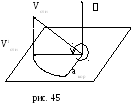 скорение
Кориолиса обращается в
скорение
Кориолиса обращается в
ноль в трёх случаях :
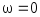 ,
т.е. когда переносное движение
,
т.е. когда переносное движение
носит поступательный характер .
2. VOTH=0.
3.![]() .
.
Направление вектора ускорения
Кориолиса определяется по правилам
векторного произведения двух векторов.
Но наиболее удобно в этих случаях воспользоваться правилом Жуковского.
Рис.45.
Правило Жуковского:
Для определения направления ускорения Кориолиса необходимо:
1. Мысленно
построить плоскость, перпендикулярную
вектору
![]() .
.
2. Спроектировать на эту плоскость относительную скорость(найти Vотн).
3. Повернуть
проекцию
![]() на
900
в плоскости в сторону переносного
вращения
(см.рис45).
на
900
в плоскости в сторону переносного
вращения
(см.рис45).
Из приведённых рассуждений следует, что ускорение Кориолиса возникает только при наличие у переносного движения угловой скорости вращения.
Кинематически ускорение Кориолиса учитывает взаимосвязь изменений относительной и переносной скоростей при их совместном повороте при вращении.
Раздел 3. Динамика.
Динамика - раздел механики, изучающий механическое движение в связи с силами, вызывающими это движение.
В теоретической механике абстрагируются от конкретных физических свойств движущихся материальных объектов и изучают движение некоторых материальных точек и твёрдых тел. Изучение динамики начнём с динамики материальной точки.
Тема 10. Дифференциальные уравнения движения материальной точки.
§ 1. Основные аксиомы динамики точки.
Как уже указывалось, в основе любых естественных наук лежат объективные законы природы, установленные опытным путём. Эти законы не доказываются, а просто фиксируются и называются аксиомами.
Динамика точки базируется на следующих аксиомах:
1. Аксиома инерции: Существует такая система отсчёта, в которой материальная точка под действием системы взаимно уравновешенных сил движется равномерно и прямолинейно по инерции(или находится в покое).
Эта аксиома впервые сформулирована Галилеем, хотя известна как 1-й закон Ньютона. Система отсчёта, в которой справедлива аксиома инерции называется инерциальной. Идеальной инерциальной системой является абсолютно неподвижная система отсчёта. Далее будет показано, что инерциальными являются и такие системы отсчёта, которые движутся поступательно прямолинейно и равномерно.
2. Аксиома пропорциональности силы и ускорения.
Ускорение материальной точки пропорционально действующей на неё силе и одинаково с ней направлено.
Рис.46.
Математическая
запись этой аксиомы имеет вид:
![]() .
.
Эта аксиома известна как 2-й закон Ньютона; часто называют её ОСНОВНЫМ ЗАКОНОМ ДИНАМИКИ материальной точки.
3. Аксиома равенства действия и противодействия.
Всякому действию существует равное и противоположно направленное противодействие.
Эта аксиома известна как 3-й закон Ньютона. При пользовании этой аксиомой следует помнить, что равенство действия и противодействия не всегда означает условие равновесия, так как действие и противодействие могут быть приложены к разным материальным точкам или телам.
4. Аксиома независимости действия сил.
Если на точку действует несколько сил, то они сообщат ей такое же ускорение, как если бы действовала одна сила, равная их равнодействующей:
![]()
Встречающийся в аксиомах коэффициент пропорциональности m между силой и ускорением называется массой материальной точки.
Масса материальной точки - скалярная величина, характеризующая меру её инертности.
