Тема 7. Плоскопараллельное (плоское) движение тела.
Плоским называется такое движение тела, при котором все его точки движутся в плоскостях, параллельных некоторой заданной плоскости (рис.21).
Из определения следует, что
в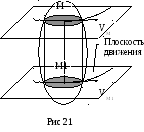
се
точки тела, лежащие на одном
перпендикуляре к плоскости
движения движутся по одинаковым
траекториям, имеют одинаковые
скорости и ускорения .
На этом основании плоское
движение тела обычно сводят к
движению плоской фигуры в плоскости
движения.
Положение плоской фигуры на плоскости однозначно определяется положением двух его любых точек А и В или положением отрезка АВ (рис.22).
Плоское движение достаточно распространено в природе и технике. Так колесо, катящееся по некоторой направляющей, совершает плоское движение. Для плоского движения можно доказать несколько теорем, более детально раскрывающих его кинематическую сущность.
Теорема 1: Плоское движение плоской фигуры в любой момент времени можно рассматривать как совокупность двух перемещений:
-- поступательного движения вместе с произвольной точкой, называемой полюсом;
-- вращательного движения относительно полюса.
Действительно, как это следует
из рис.23, новое положение фигуры
п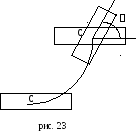
ри
плоском движении путём можно
получить путем поступательного
вместе с произвольным полюсом с
и последующим поворотом её
относительно полюса на
угол . Заметим, что последова-
тельность перемещений не имеет
значения. Отметим ещё одно важное
обстоятельство: угол поворота в
новом положении не зависит от выбора
полюса.
Приведённые рассуждения позволяют составить кинематические уравнения плоского движения фигуры. Они представляют собой систему уравнений, описывающих движение полюса С, и вращательное движение относительно полюса:
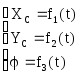
Поскольку, как
указывалось, угол поворота не зависит
от выбора полюса, то и его производные
и
также не зависят от выбора полюса. Их
называют:
- угловая скорость плоского движения;
- угловое ускорение плоского движения.
Теорема 2: Скорость любой точки фигуры при плоском движении равна геометрической сумме скорости полюса и скорости при вращении относительно полюса.
Утверждение этой теоремы базируется на выводах предыдущей теоремы. Действительно, если плоское движение есть совокупность поступательного и вращательного движений, то и скорость любой точки фигуры складывается из скоростей поступательного и вращательного движений. Доказательство можно провести и более строго:
Выберем за полюс точку А со
скоростью
.
Фигура, двигаясь плоско,
вращается с угловой скоростью .
Движение точек А и В фигуры
определим
радиусами-векторами
и
относительно неподвижного центра О
(рис.24). Из рисунка :
В этом выражении
векторы
и
могут изменяться произвольно, вектор же
может только
поворачиваться; модуль его неизменен,
поскольку он соединяет две точки
недеформируемого тела. Для перехода к
скоростям продифференцируем записанное
выражение:
или
,
где
-
вращательная скорость точки В относительно
точки А.
Таким образом:
На основании этой теоремы можно сформулировать простое правило вычисления скорости любой точки тела при плоском движении, если известна скорость какой - либо другой точки тела и угловая скорость:
1.Выберем за полюс точку тела, скорость которой известна (точка А на рис.25).
2.В искомой точке В отложим вектор скорости полюса А (при поступательном движении скорости всех точек одинаковы).
3.Вычислим вращательную скорость точки В относительно полюса А
V
BA=*AB
и отложим её перпендикулярно АВ,
направив вектор
по направлению
вращения.
4.Вычислим скорость точки В по
формуле:
.
Доказанная теорема подтверждает справедливость
основной теоремы кинематики твёрдого
тела (см. выше) применительно к плоскому
движению .
Проекции скоростей двух точек на
линию, проходящую через эти точки,
равны между собой (рис.26). Так как
,то
.
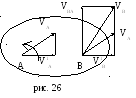
Теорема 3: Ускорение любой точки фигуры при плоском движении равно геометрической сумме ускорения полюса и ускорения при вращении относительно полюса.
Доказательство этой теоремы легко получается на основании соотношения, полученного в предыдущей теореме.
Имеем:
Дифференцируем по времени:
или
,
где
-
вращательное ускорение точки В
относительно А.
-
центростремительное ускорение точки
В относительно А.
Таким образом,
.
На основании этой теоремы можно
сформулировать простое правило
вычисления ускорения любой точки
тела при плоском движении, если известно
ускорение какой-либо другой точки,
угловая скорость и угловое ускорение .
1.Выберем за полюс точку тела, ускорение
которой известно (точка А на рис.27).
2.В искомой точке В отложим вектор
у
скорения
полюса А (при поступательном
движении ускорения всех точек одинаковы).
3.Вычислим вращательное ускорение точки
В относительно
полюса А
и отложим его
перпендикулярно АВ, направив вектор
по направлению углового ускорения.
4.Вычислим центростремительное ускорение точки В относительно полюса А
(
)
и отложим его по линии АВ от точки В к
А.
5.Вычислим ускорение точки В по формуле:
При решении некоторых задач на плоское движение полезной оказывается теорема о существовании мгновенного центра скоростей.
Теорема 4: При плоском движении фигуры в каждый момент времени существует точка, скорость которой равна нулю. Эта точка называется мгновенным центром скоростей(МЦС).
Возьмём две произвольные точки
фигуры со скоростями
и
.
Проведём
перпендикуляры к скоростям, которые
пересекутся, например, в точке О (рис.28).
Эта точка О имеет нулевую скорость, т.е.
является МЦС. В противном случае не
будет выполняться основная теорема
кинематики твёрдого тела о равенстве
проекций скоростей точек тела на линию,
п
роходящую
через эти точки.
При использовании МЦС в качестве
полюса заметно упрощается задача по определению
скоростей точек тела.
Например, при
полюсе А со скоростью
:
при полюсе О со скоростью Vo=0:
Замечаем, что плоское движение фигуры относительно МЦС сводится к мгновенному вращению. Необходимо отметить, что в мгновенном центре скоростей ускорение точки фигуры не равно нулю, поэтому приведённые выше рассуждения нельзя распространять на задачу по определению ускорений. Можно показать, что наряду с МЦС, в каждый момент времени существует и мгновенный центр ускорений (МЦУ). Координаты МЦС и МЦУ не совпадают.
Итак, задача по определению скоростей точек фигуры при плоском движении упрощается при использовании МЦС в качестве полюса.
Отыскание же местоположения самого МЦС на плоскости движения в ряде случаев особой трудности не представляет.
Рис.29.
Так на рис. 29 (а) положение МЦС определяется как точка пересечения перпендикуляров к скоростям в точках А и В стержня АВ, совершающего плоское движение.
На рис. 29 (б) положение МЦС определяется в точке контакта К неподвижного рельса и колеса, совершающего плоское движение.
В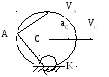
заключение рассмотрим пример определения
скорости и ускорения точки А колеса,
катящегося без скольжения по горизонтальному
основанию.
Пример:
Дано: Центр колеса С движется со
скоростью
и ускорением
.
Определить: Скорость и ускорение
точки А колеса.
Решение:
1. Зная положение МЦС (точка К), найдём угловую скорость колеса:
2. Найдём скорость точки А по формуле:
(вектор
скорости
).
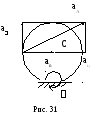
Рис.31.
3. Найдём угловое ускорение колеса:
4. Найдём вращательное ускорение точки А:
(вектор
)
5. Найдём центростремительное ускорение точки А:
(вектор
направлен от
точки А к С)
6. Находим полное ускорение точки А:
).