§ 2. Принцип возможных (виртуальных) перемещений.

Принцип возможных перемещений применяется для анализа условий равновесия механических систем с идеальными связями. Если механическая система находится в равновесии, то это означает, что все её материальные точки, находящиеся под действием задаваемых сил и сил реакции, находятся в равновесии. Следовательно, условие статического равновесия точек системы опишется уравнениями:

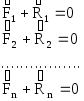
Хотя механическая система и находится в равновесии, мысленно зададим одной из точек системы малое перемещение в направлении, допускаемом её связью. При этом все или часть других точек получат соответствующие малые перемещения. Следовательно, приложенные к ним силы мысленно выполнят элементарные работы, сумма которых равна нулю.

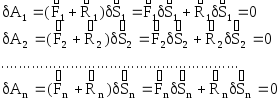
Или

Если механическая система имеет только идеальные связи, то по определению.

Таким образом: Если механическая система с идеальными связями находится в равновесии, то при любом мысленном малом возможном перемещении системы сумма работ всех задаваемых сил равна нулю.

Уравнение вида называется общим уравнением статики.

Примечание 1: Под малым возможным перемещением точек механической системы, с математической точки зрения, понимается величина первого порядка малости. Это допущение позволяет в целях упрощения пренебрегать малыми величинами более высоких порядков, например:

и т.д.

Примечание 2: Если механическая система имеет z степеней свободы, то полное равновесие по всем степеням свободы описывается числом z общих уравнений статики.

Запишем общее уравнение статики для простейшего механизма:

или

Эти соотношения позволяют сформулировать “золотое правило” механики: Сколько выиграно в силе, столько проиграно в расстоянии ( в скорости).

§ 3. Общее уравнение динамики.

Принцип возможных перемещений можно применять и в случаях, когда механическая система не находится в равновесии. Однако в этом случае к материальным точкам системы, наряду с задаваемыми силами и силами реакции связей, для получения динамического равновесия по Даламберу, следует прикладывать силы инерции.

Запишем уравнения динамического равновесия точек системы:

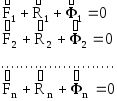
Зададим системе мысленное малое возможное перемещение, при этом силы, приложенные к её точкам, выполнят элементарные работы, сумма которых равна нулю.

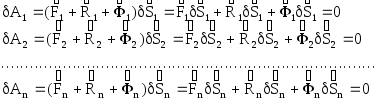
или

Если механическая система имеет только идеальные связи, то по определению.

Таким образом: Для всякой механической системы с идеальными связями сумма элементарных работ всех задаваемых сил и сил инерции, условно приложенных к точкам системы, равна нулю.

Уравнение вида называется общим уравнением динамики.

Общее уравнение динамики обычно используется для вычисления ускорений точек механической системы.

Примечание: Если механическая система имеет z степеней свободы, то для описания её полного движения требуется составить z общих уравнений динамики.

§ 4. Уравнение Лагранжа II рода.

Ускорение точек механической системы можно определять и с помощью уравнения Лагранжа II рода, являющегося дифференциальным уравнением механической системы.

Получим это уравнение для механической системы с одной степенью свободы.

Пусть механическая система задана обобщённой координатой q(t). Радиус - вектор произвольной i-той точки системы можно соответствующим образом вычислить через обобщённую координату

Тогда скорость этой точки определим:

Следовательно, вектор скорости произвольной i - той точки в общем случае зависит как от обобщённой координаты q, так и от обобщённой скорости

Кинетическая энергия механической системы равна сумме кинетических энергий её материальных точек.

Учитывая эту функциональную зависимость, найдём частные производные от кинетической энергии по обобщённой координате q и обобщённой скорости

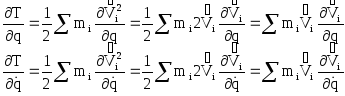
по правилу Лопиталя

Таким образом:

Продифференцируем последнее уравнение по времени:

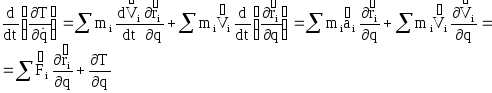
Таким образом:

=

Рассмотрим физический смысл выражения, стоящего в правой части полученного уравнения.

=- есть сумма элементарных работ задаваемых сил, приложенных к точкам системы. Эту сумму работ можно представить как некоторую обобщённую силу Q механической системы, умноженную на элементарное перемещение обобщённой координаты, т.е.

=Q_i

Следовательно, /- обобщённая сила системы.

Окончательно получим уравнение Лагранжа II рода:

= Q

Примечание: Если механическая система имеет z степеней свободы, то для описания её полного движения требуется составить z уравнений Лагранжа II рода:

. . . . . . . . . . . .

При использовании уравнений Лагранжа II рода рекомендуется придерживаться следующей последовательности:

1. Изобразить на рисунке механической системы активные силы( и моменты от пар сил).

2. Выбрать обобщённую координату.

3. Выразить кинетическую энергию системы через обобщённую скорость и обобщённую координату.

4. Вычислить обобщённую силу системы, для чего определить сумму элементарных работ всех активных сил и разделить её на приращение обобщённой координаты.

5. Решить уравнение Лагранжа II рода.