§ 5. Применение методов аналитической механики для анализа поведения механических систем в некоторых частных случаях.

А: Исследование условий равновесия механических систем.

При рассмотрении принципа возможных перемещений было показано, что условием равновесия механической системы с идеальными связями, имеющей z степеней свободы, является равенство нулю элементарных работ задаваемых сил по всем степеням свободы:

;; . . . .

Но как показано в § е 3 темы 4, элементарная работа потенциальных сил равна элементарному изменению потенциальной энергии, взятой с обратным знаком, т.е.

; ;

где q₁; q₂;...q_z - соответствующие обобщённые координаты.

Следовательно, можно записать:

dП=, где

dП - полный дифференциал потенциальной энергии механической системы.

Следовательно, для механической системы с потенциальными силами условием равновесия может служить dП=0.

Математически это означает, что потенциальные силы обеспечивают равновесие системы в тех случаях, когда потенциальная энергия находится в экстремуме по отношению к обобщённым координатам.

При этом равновесие может быть

устойчивым и неустойчивым. Из рис.97 можно наглядно уяснить признак устойчивости равновесия

( признак Лагранжа-Дирихле):

“ Потенциальная система находитсяустойчивом равновесии

в окрестности минимума потенциальной энергии”.

Пример: Исследовать, при каких значениях обобщённых координат потенциальная механическая система с двумя степенями свободы находится в устойчивом равновесии.

Дано: m₁ - масса стержня;

l - длина стержня;

S₀ - собственная длина пружины;

C - коэффициент жёсткости пружины;

m₂ - масса груза.

Выбираем обобщённые координаты:

q₁=; q₂=S

Найдём условия равновесия по  и S.

Для этого запишем выражение для потенциальной энергии относительно оси

подвеса О:

а) Исследуем равновесие по :

Условиями равновесия является sin=0 (₁=0; ₂=)

Условием устойчивого равновесия является  0, т.е.

0 при =0.

б) Исследуем равновесие по S:

S_{равнов.}=

0 - устойчивость равновесия обеспечивается при любой статической деформации пружины.

Так при =0 S_ст=

при =S_ст= -

Б: Применение уравнений Лагранжа II рода для исследования колебаний механических систем.

В теме 11 рассматривались колебания материальной точки. В частности было показано, что свободные колебания с учётом вязкости описываются дифференциальным уравнением:

, где 2n=;

При n k решение этого уравнения имеет вид:

или

, где

Механические системы под действием восстанавливающих сил также могут совершать колебания относительно равновесного положения.

Рассмотрим пример исследования таких колебаний для механических систем с одной степенью свободы.

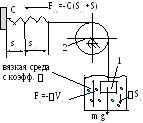Дано: m₁; m₂; C; .

Определить период затухающих

колебаний.

Замечаем, что S_ст=.

Для решения используем уравнение

Лагранжа II рода.

Рис.99.

В качестве обобщённой координаты выберем S₁.

Итак q=S₁; .

Найдём кинетическую энергию системы:

;

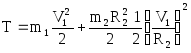; =a₁= ;

Найдём обобщённую силу системы, для чего зададим ей малое возможное перемещение S₁.

=

, где m₁g=CS_ст, так что

Q₁=

Окончательно уравнение Лагранжа II рода в данном случае запишется:

=или

Перепишем его в каноническом виде:

, где .

Искомый период: T=.

69