§ 3. Теорема о движении центра масс механической системы.

Существуют задачи, в которых исследование движения механической системы сводится к закону движения лишь одной её характерной точки - центра масс. Дифференциальное уравнение движения центра масс механической системы легко можно получить из системы уравнений (1), описывающих движение её материальных точек.

Сложив почленно слагаемые, будем иметь:

Учитывая, что радиус-вектор центра масс определяется выражением:

или

После двойного дифференцирования будем иметь:

Кроме того учтём, что

Окончательно получим:

Полученное соотношение позволяет сформулировать Теорему о движении центра масс механической системы:

Центр масс механической системы движется как одна материальная точка с массой системы, в которой приложены все внешние силы.

Рассмотренная теорема имеет важные следствия:

1. Внутренние силы не могут изменить характер движения центра масс механической системы.

2. Пара сил, приложенная к твёрдому телу не может изменить характер движения его центра масс.

3. Если главный вектор внешних сил механической системы равен нулю, то её центр масс находится в покое, либо движется прямолинейно и равномерно ( по инерции).

§ 4. Понятие о моментах инерции твёрдого тела.

Как известно, масса тела является мерой инертности тела. При движениях, связанных с вращением тела относительно полюса или оси определяющим в инерционных свойствах становится не сама масса, а закон её распределения относительно полюса или оси.

Скалярная величина, характеризующая закон распределения её массы относительно полюса или оси, называется моментом инерции.

В соответствии с определением различают:

- момент инерции относительно полюса I₀ (полярный момент инерции);

- моменты инерции относительно координатных осей I_X,I_Y,I_Z (осевые моменты инерции).

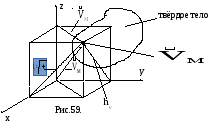
Моменты инерции тела равны сумме произведений масс точек тела на квадрат расстояния до полюса или соответствующих осей (рис.61).

I₀=

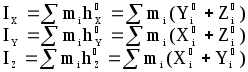
Легко убедиться, что I_X+I_y+I_Z=2*I₀.

Примечание: Если твёрдое тело - плоская фигура, располагающаяся в плоскости XY, то для всех точек фигуры Z _i=0. Следовательно,

Следовательно, I_Z=I₀.

Таблица 1.

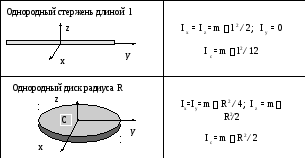
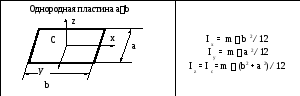
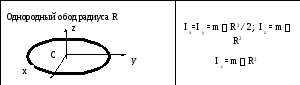
Моменты инерции тел могут быть получены либо расчётным, либо опытным путём и приводятся в специальных справочниках. В таблице 1 приведены моменты инерции некоторых тел относительно координатных осей, проходящих через начало координат:

Момент инерции твёрдого тела относительно заданной точки или оси, например оси Z, можно представить в виде произведения массы тела на квадрат линейной величины, называемой радиусом инерции тела относительно этой оси (точки).

Эта формула показывает, что радиус инерции определяет расстояние от оси Z до точки, в которой нужно сосредоточить всю массу тела чтобы момент инерции точки был равен моменту инерции тела.

Единицей измерения момента инерции является 1 кГм².

Оси координат, проходящие через центр тяжести тела, называются центральными. Для пересчёта моментов инерции на нецентральные оси пользуются теоремой Штейнера.

Теорема Штейнера: Момент инерции относительно нецентральной оси равен моменту инерции относительно параллельной ей центральной оси плюс произведение массы тела на квадрат расстояния между осями.

Действительно, из рис.60 следует:

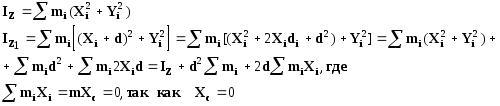
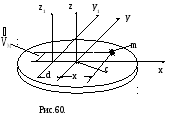
Окончательно, .