
- •Основные обозначения.
- •1. Элементарные сведения.
- •Контрольные задания
- •2. Комплексные числа.
- •555 Решение алгебраических уравнений.
- •3. Линейная алгебра. Матрицы и основные операции с ними.
- •Определители 2-го и 3-го порядка.
- •Решение систем линейных уравнений с помощью определителей.
- •Контрольные задания
- •4. Аналитическая геометрия. Системы координат на плоскости и в пространстве.
- •Векторы и линейные операции над ними.
- •Скалярное, векторное и смешанное произведения векторов.
- •555 Прямая на плоскости и различные способы её задания.
- •555 Прямая и плоскость в пространстве и различные способы их задания.
- •555 Линии второго порядка.
- •555 Некоторые поверхности второго порядка.
- •Контрольные задания
- •5. Функции одного аргумента. Понятие функции и способы задания.
- •Предел функции и числовой последовательности.
- •Понятие числового и степенного ряда.
- •Непрерывность функции, точки разрыва.
- •Контрольные задания
- •6. Производная и дифференциал.
- •555 Приближенное решение уравнений.
- •Контрольные задания
- •7. Неопределенный интеграл.
- •Свойства неопределённых интегралов.
- •Контрольные задания
- •8. Определенный интеграл.
- •Приложения определённого интеграла:
- •9. Функции нескольких аргументов.
- •10. Дифференциальные уравнения.
- •Методы решения основных типов дифференциальных уравнений первого порядка.
- •11. Общая задача линейного программирования.
- •Контрольные задания
- •Приложение. Задачи для подготовки к экзамену.
- •Учебная литература.
Контрольные задания
Найти точки разрыва функции
13.1 y =
![]() 13.2
y =
13.2
y =![]()
13.3 y = |x-5|(x+2) 13.4 y = ln|(x-5)(x-3)|
13.5 y =
![]() 13.6
y = log|(x-2)(x+5)|x
13.6
y = log|(x-2)(x+5)|x
13.7 y = |x+3|(x+4) 13.8
y =
![]()
13.9 y = log|(x-4)(x+1)|x 13.10 y = log|(x+2)(x-3)|x
13.11 y =
ln|(x-2)(x+5)| 13.12 y =
![]()
13.13 y = log|(x+2)(x+4)|x 13.14 y = tg(4x)-tg(4x)
13.15 y = |x-2|x+1 13.16 y = -tg(4x)+tg(2x)
13.17 y =
ln|(x+4)(x-4)| 13.18 y =
![]()
13.19 y = -tg(5x)-tg(x) 13.20 y = log|(x+2)(x+5)|x
13.21 y = log|x+4||x+5| 13.22 y = ln|(x-1)(x+3)|
13.23 y = log|(x+5)(x+3)|x 13.24 y = tg(2x)-tg(4x)
13.25 y = |x-4|x-2 13.26 y = tg(3x)-tg(2x)
13.27 y = log|x+1||x-1| 13.28 y = ln|(x+5)(x+4)|
13.29 y =
![]() 13.30
y =
13.30
y =![]()
13.31 y =
![]() 13.32
y = |x-2|x+3
13.32
y = |x-2|x+3
13.33 y = -tg(3x)-tg(x) 13.34 y = log|(x+3)(x+4)|x
13.35 y = log|x+5||x-3|
Найти пределы
14.1
![]()
![]()
14.2
![]()
![]()
14.3
![]()
![]()
14.4
![]()
![]()
14.5
![]()
![]()
14.6
![]()
![]()
14.7
![]()
![]()
14.8
![]()
![]()
14.9
![]()
![]()
14.10
![]()
![]()
14.11
![]()
![]()
14.12
![]()
![]()
14.13
![]()
![]()
14.14
![]()
![]()
14.15
![]()
![]()
14.16
![]()
![]()
14.17
![]()
![]()
14.18
![]()
![]()
14.19
![]()
![]()
14.20
![]()
![]()
14.21
![]()
![]()
14.22
![]()
![]()
14.23
![]()
![]()
14.24
![]()
![]()
14.25
![]()
![]()
14.26
![]()
![]()
14.27
![]()
![]()
14.28
![]()
![]()
14.29
![]()
![]()
14.30
![]()
![]()
14.31
![]()
![]()
14.32
![]()
![]()
14.33
![]()
![]()
14.34
![]()
![]()
14.35
![]()
![]()
6. Производная и дифференциал.
Производной
называется предел отношения приращения
функции к приращению аргумента, когда
последний стремится к нулю:
![]()
Геометрический смысл - тангенс угла наклона касательной.
Дифференциалом функции называется выражение dy=y¢dx.
Правила дифференцирования и таблица производных.
Основные свойства производных (правила дифференцирования):
1) c¢=0
2) (y±z)¢=y¢±z¢
3) (yz)¢=y¢z+yz¢, в частности (cy)¢=cy¢
4)
![]() ,
в частности
,
в частности
![]()
5)
![]()
6) (f(g(x)))¢=f¢(g(x))g¢(x), в частности (f(ax+b))¢=af¢(ax+b)
Таблица производных:
x¢=1 (xn)¢=nxn-1,
в частности
![]()
(ex)¢=ex (ax)¢=lnaax
(sinx)¢=cosx (cosx)¢=-sinx
![]()
![]()
![]()
![]()
Производные высших порядков.
При повторном дифференцировании производных получаются производные 2-го, 3-го, ... порядков. Они обозначаются так: y², y¢¢¢, yIV, и т.д., а в общем случае y(n)
Пример 1.
y=sin(x2) y¢=2xcos(x2) y²=2cos(x2)-4x2sin(x2)
666
Найти производную и дифференциал:
1. y = x3 - 3x + 1 Решение: y¢ = 3x2 - 3 Þ dy = (3x2 - 3)dx (используем свойства 2, 3, таблицу и определение дифференциала)
2.
y = 3x![]() - 2x2
+
- 2x2
+
![]() Указание
Указание
![]()
3. y = 2x + log2x 4. y = 3-x + x-3
5. y = xsinx + 2cosx 6. y = tg2x
7.
y =
![]() 8. y =
8. y =![]()
9. y = arcsinx - arccosx 10. y = sin(x2)
11.
y = x![]() 12.
y = 2ln(2tgx)
12.
y = 2ln(2tgx)
Найти производную 2-го порядка:
13. y = arctgx 14. y = ln(x2 + 1)
15.
y = cos![]() 16.
y = sinx×lnx
16.
y = sinx×lnx
555
Приложения производной.
Формула Лагранжа: если функция y=f(x) дифференцируема на отрезке [a,b], то $ сÏ(a,b), что f(b) - f(a) = (b - a)f¢(c).
Правило Лопиталя:
если
![]() или
или![]() ,
то
,
то![]()
Если f¢(x)>0, то f(x) возрастает, а если f¢(x)<0, то f(x) убывает.
Если при переходе через точку x0 производная f¢(x) меняет знак, то в этой точке экстремум. Это оформляется например так:
|
- + + - - x
min max на рисунке указаны знаки производной f¢(x) |
Если при переходе через точку x0 вторая производная f²(x) меняет знак, то в этой точке перегиб. Это оформляется например так:
|
- + + - - x
перегиб перегиб на рисунке указаны знаки второй производной f²(x) |
Общая схема исследования функций:
1) Находим область определения и множество значений.
2) Определяем чётность-нечётность, периодичность, точки пересечения с осями координат.
3) Находим асимптоты и точки пересечения с ними.
4) Находим производную и экстремумы.
5) Находим производную второго порядка и перегибы.
6) Находим особенности, не входящие в пункты 1¸6.
7) Строим график функции.
666
Найти предел:
17.
![]() Решение:
Решение: ![]() (два раза применили правило Лопиталя и
затем замечательный предел)
(два раза применили правило Лопиталя и
затем замечательный предел)
18.
![]() 19.
19.
![]()
Найти экстремумы:
20. y = 5x3 - 15x Решение: y¢ = 15x2 - 15 15x2 - 15 = 0 x1,2=±1
|
+ - + x
max min |
Ответ: ymax = 10 при x = -1 ymin = -10 при x = 1 |
21. y = ln2×3-x + ln3×2x 22. y = cos2x + 4cosx
Найти точки перегиба:
23. y = x4 - 6x2 + 8 24. y =x3e-x
Исследовать функцию и построить график
25.
y =
![]() 26.
y = x
26.
y = x![]()
27.
y =
![]() 28.
y =
28.
y =![]()











 Ç
È
È
Ç
Ç
Ç
È
È
Ç
Ç
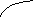






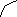
 -1
1
-1
1