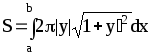- •Основные обозначения.
- •1. Элементарные сведения.
- •Контрольные задания
- •2. Комплексные числа.
- •555 Решение алгебраических уравнений.
- •3. Линейная алгебра. Матрицы и основные операции с ними.
- •Определители 2-го и 3-го порядка.
- •Решение систем линейных уравнений с помощью определителей.
- •Контрольные задания
- •4. Аналитическая геометрия. Системы координат на плоскости и в пространстве.
- •Векторы и линейные операции над ними.
- •Скалярное, векторное и смешанное произведения векторов.
- •555 Прямая на плоскости и различные способы её задания.
- •555 Прямая и плоскость в пространстве и различные способы их задания.
- •555 Линии второго порядка.
- •555 Некоторые поверхности второго порядка.
- •Контрольные задания
- •5. Функции одного аргумента. Понятие функции и способы задания.
- •Предел функции и числовой последовательности.
- •Понятие числового и степенного ряда.
- •Непрерывность функции, точки разрыва.
- •Контрольные задания
- •6. Производная и дифференциал.
- •555 Приближенное решение уравнений.
- •Контрольные задания
- •7. Неопределенный интеграл.
- •Свойства неопределённых интегралов.
- •Контрольные задания
- •8. Определенный интеграл.
- •Приложения определённого интеграла:
- •9. Функции нескольких аргументов.
- •10. Дифференциальные уравнения.
- •Методы решения основных типов дифференциальных уравнений первого порядка.
- •11. Общая задача линейного программирования.
- •Контрольные задания
- •Приложение. Задачи для подготовки к экзамену.
- •Учебная литература.
Контрольные задания
В первом задании написать функцию, которая должна стоять в скобках, а во втором и третьем - найти интегралы
18.1
![]()
18.2
![]()
18.3
![]()
18.4
![]()
18.5
![]()
18.6
![]()
18.7
![]()
18.8
![]()
18.9
![]()
18.10
![]()
18.11
![]()
18.12
![]()
18.13
![]()
18.14
![]()
18.15
![]()
18.16
![]()
18.17
![]()
18.18
![]()
18.19
![]()
18.20
![]()
18.21
![]()
18.22
![]()
18.23
![]()
18.24
![]()
18.25
![]()
18.26
![]()
18.27
![]()
18.28
![]()
18.29
![]()
18.30
![]()
18.31
![]()
18.32
![]()
18.33
![]()
18.34
![]()
18.35
![]()
8. Определенный интеграл.
Пусть на отрезке
[a;b]
задана
функция f(x).
Разобьём
отрезок на n
частей точками a=x0<x1<x2<...<xn-1<xn=b.
На
каждой части возьмём точки h1,
h2,
h3,
... hn
соответственно
и составим сумму
![]() ,
или короче
,
или короче![]() .
Если существует предел этой суммы, когда
длины всех частей стремятся к нулю, то
он называется определённым интегралом
от функцииf(x)
на
отрезке [a;b]
и
обозначается
.
Если существует предел этой суммы, когда
длины всех частей стремятся к нулю, то
он называется определённым интегралом
от функцииf(x)
на
отрезке [a;b]
и
обозначается
![]() .Свойства
определённого интеграла.
.Свойства
определённого интеграла.
1)
![]() ,
где F(x)
- первообразная
для f(x)
(формула
Ньютона-Лейбница)
,
где F(x)
- первообразная
для f(x)
(формула
Ньютона-Лейбница)
2)
![]()
3)
![]()
4)
![]() (интегрирование
по частям)
(интегрирование
по частям)
5)
![]() ,
где a=j(a)
и b=j(b)
(замена переменной)
,
где a=j(a)
и b=j(b)
(замена переменной)
6)
![]()
7) если a<b
и
f(x)³0,
то
![]() Þ
если a<b
и
f(x)£g(x),
то
Þ
если a<b
и
f(x)£g(x),
то
![]()
8) если f(x)
непрерывна
на [a;b],
то
![]() ,
где сÎ(a;b)
(теорема о среднем)
,
где сÎ(a;b)
(теорема о среднем)
Приложения определённого интеграла:
|
Площадь плоской фигуры, ограниченной линиями: x=a, x=b³a, y=f(x)³0, y=0 |
|
|
Площадь плоской фигуры, ограниченной линиями: x=a, x=b³a, y=f(x), y=g(x)³f(x) |
|
|
Площадь плоской фигуры в полярной системе координат, ограниченной линиями: j=a, j=b³a, r=r(j)³0 |
|
|
Длина
плоской линии, заданной параметрически:
|
|
|
Длина плоской линии, заданной уравнением: y=f(x), a£x£b |
|
|
Длина плоской линии в полярной системе координат: r=r(j), a£j£b |
|
|
Объём тела, полученного вращением фигуры 0£y£f(x), a£x£b вокруг оси Ox |
|
|
Аналогично вокруг оси Oy |
|
|
Площадь поверхности, образованное вращением линии y=f(x), a£x£b вокруг оси Ox |
|
|
Аналогично вокруг оси Oy |
|
666
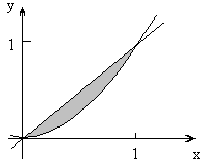
Вычислить площадь фигуры:
1. y = x2; y=x
|
Решение:
x=x2
Þ
x1=0,
x2=1
S= |
|
2. y = x3 - x; y = 0 3. y = x5 - 9x3
4.
r = j(p
- j),
0£j£p 5.
r =
![]()
Вычислить объём тела вращения:
6. y = x2; y2 = x вокруг оси Ox и Oy
7. y = x; y3 = x вокруг оси Ox и Oy
Вычислить длину линии:
8. 9y2 = 4x3, x£15 9. y = 0,5(ex + e-x), 0£x£ln2
10. x=1-cost, y=sint 11. r = e-j, 0£j£2p
12. x=cos3t, y=sin3t, 0£t£p/2 13. r = cosj, |j|£p/2
Вычислить площадь поверхности вращения:
14
y=![]() ,
xÎ[-5;7] 15.
y = 0,5(ex
+ e-x)
xÎ[0;ln2]
,
xÎ[-5;7] 15.
y = 0,5(ex
+ e-x)
xÎ[0;ln2]
555
Несобственные интегралы.
Если один из
пределов интегрирования бесконечность,
то интеграл называется несобственным
интегралом первого рода и обозначается
так:
![]()
Если подынтегральная функция в одной или нескольких точках отрезка [a;b] имеет разрыв, то интеграл называется несобственным интегралом второго рода и обозначается как обычный определённый интеграл.
666
Вычислить несобственные интегралы:
16.
![]() Решение:
Решение: 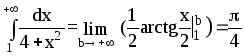
17.
![]() 18.
18.
![]()
19.
![]() 20.
20.
![]()
555
Приближенное вычисление определенных интегралов.
Разобьём отрезок интегрирования на n равных частей точками x0, x1, x2, ..., xn: a=x0<x1<...<xn=b. Обозначим h=(b - a)/n.
|
Формула прямоугольников |
|
|
Формула трапеций |
|
|
Формула Симпсона (n - чётное) |
|
666
Вычислить приближённо с точностью до 0,001:
21.
![]() 22.
22.![]()
23.
![]() Указание:
считать,
что xx=1
при
x=0
Указание:
считать,
что xx=1
при
x=0
24.
![]() 25.
25.
![]()
555
|
Выучить наизусть |
|
Определение определённого интеграла. Свойства определённого интеграла. Формулы приложений определённого интеграла. |
Ответы:
2.
0,5 3. 120,5 4.
![]() 5.
1 6. Ox: 0,3p;
Oy: 0,3p
5.
1 6. Ox: 0,3p;
Oy: 0,3p
7.
Ox:
![]() ;
Oy:
;
Oy:![]() 8.
42 9. 0,75 10.p 11.
8.
42 9. 0,75 10.p 11.
![]() (1-e-2p)
(1-e-2p)
12. 1,5 13. p 14. 43p 15. (0,9375 + ln2)p 17. p
18.
![]() 19.
0,5 20. -1
19.
0,5 20. -1
Контрольные задания
Найти площадь плоской фигуры, ограниченной линиями:
19.1 y=x2+x; y=2x 19.2 y=x2-x; y=2x
19.3 y=sinx; y=-sinx; 0£x£p 19.4 y=ex; y=1+(e-1)x
19.5
y=ex+e-x;
y=e+e-1 19.6
y=x![]() ; x=y
; x=y![]()
19.7
y=![]() ;
x=
;
x=![]() 19.8
y=x-x3;
y=0
19.8
y=x-x3;
y=0
19.9 y2=(10-x)3; x=0 19.10 (10-y)3=x2; y=0
19.11 y2=(10-x)5; x=0 19.12 (10-y)5=x2; y=0
Найти длину линии:
20.1
![]() 20.2
20.2![]()
20.3 y=ln(cosx); 0£x£p/3 20.4 y=ln(sinx); p/6£x£5p/6
20.5 r=e-j; |j|£ln2 20.6 r=cosj; |j|£p/2
20.7 r=sinj; 0£j£p 20.8 x=sint; y=cost; 0£t£p/2
20.9 x=1-sint; y=cost; 0£t£p/2 20.10 x=1-cost; y=sint; 0£t£p/2
20.11 x=1+sint; y=cost; 0£t£p/2 20.12 x=1+cost; y=sint; 0£t£p/2
Найти площадь поверхности вращения вокруг указанной оси:
21.1 вокруг ox y=5x+1, 0£x£1 21.2 вокруг ox y=5x-1, 1£x£3
21.3 вокруг ox y=-5x+1, -2£x£-1 21.4 вокруг ox y=-5x-1, -1£x£0
21.5 вокруг ox y2=x+1, -1£x£0 21.6 вокруг ox y2=x-1, 1£x£2
21.7 вокруг oy y=x2, 0£y£1 21.8 вокруг oy y=x2-1, -1£y£0
21.9 вокруг oy y=x2+1, 1£y£2 21.10 вокруг oy y=5x2, 0£y£20
21.11 вокруг oy y=x2-1, -1£y£3 21.12 вокруг oy y=7x2, 0£y£7
Найти объём тела вращения вокруг указанной оси:
22.1 вокруг ox y=sinx; 0£x£p 22.2 вокруг ox y=cosx; 0£x£p
22.3 вокруг ox y=tgx; 0£x£p/4 22.4 вокруг ox y=ctgx; p/4£x£p/2
22.5 вокруг ox y=sinx+cosx; 0£x£p 22.6 вокруг oy x=siny; 0£y£p
22.7 вокруг oy x=cosy; 0£y£p 22.8 вокруг oy x=tgy; 0£y£p/4
22.9 вокруг oy x=ctgy; p/4£y£p/2 22.10 вокруг oy x=siny+cosy; 0£y£p
22.11 вокруг oy x=tgy+ctgy; p/6£y£p/3
22.12 вокруг oy x=siny-cosy; 0£y£p
Вычислить с точностью 0,0001 по формуле Симпсона:
23.1
![]() 23.2
23.2![]() 23.3
23.3![]()
23.4![]() 23.5
23.5![]() 23.6
23.6![]()
23.7![]() 23.8
23.8![]() 23.9
23.9![]()
23.10![]() 23.11
23.11
![]() 23.12
23.12![]()
23.13![]() 23.14
23.14![]() 23.15
23.15![]()
23.16![]() 23.17
23.17![]() 23.18
23.18![]()
23.19![]() 23.20
23.20![]() 23.21
23.21
![]()
23.22![]() 23.23
23.23![]() 23.24
23.24![]()
23.25![]() 23.26
23.26![]() 23.27
23.27![]()
23.28![]() 23.29
23.29![]() 23.30
23.30![]()
23.31
![]() 23.32
23.32![]() 23.33
23.33![]()
23.34![]() 23.35
23.35![]()

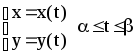
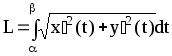

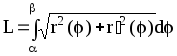
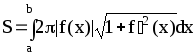 или кратко
или кратко