
- •Основные обозначения.
- •1. Элементарные сведения.
- •Контрольные задания
- •2. Комплексные числа.
- •555 Решение алгебраических уравнений.
- •3. Линейная алгебра. Матрицы и основные операции с ними.
- •Определители 2-го и 3-го порядка.
- •Решение систем линейных уравнений с помощью определителей.
- •Контрольные задания
- •4. Аналитическая геометрия. Системы координат на плоскости и в пространстве.
- •Векторы и линейные операции над ними.
- •Скалярное, векторное и смешанное произведения векторов.
- •555 Прямая на плоскости и различные способы её задания.
- •555 Прямая и плоскость в пространстве и различные способы их задания.
- •555 Линии второго порядка.
- •555 Некоторые поверхности второго порядка.
- •Контрольные задания
- •5. Функции одного аргумента. Понятие функции и способы задания.
- •Предел функции и числовой последовательности.
- •Понятие числового и степенного ряда.
- •Непрерывность функции, точки разрыва.
- •Контрольные задания
- •6. Производная и дифференциал.
- •555 Приближенное решение уравнений.
- •Контрольные задания
- •7. Неопределенный интеграл.
- •Свойства неопределённых интегралов.
- •Контрольные задания
- •8. Определенный интеграл.
- •Приложения определённого интеграла:
- •9. Функции нескольких аргументов.
- •10. Дифференциальные уравнения.
- •Методы решения основных типов дифференциальных уравнений первого порядка.
- •11. Общая задача линейного программирования.
- •Контрольные задания
- •Приложение. Задачи для подготовки к экзамену.
- •Учебная литература.
2. Комплексные числа.
Множество всевозможных пар действительных чисел называется множеством комплексных чисел, если выполняются условия:
1) определено сравнение (a,b)=(c,d) Û a=c Ù b=d
2) определено cложение (a,b)+(c,d)=(a+c,b+d)
3) определено умножение (a,b)(c,d)=(ac-bd,ad+bc)
При этом число (0,0) называется нулём и обозначается 0, число (1,0) называется единицей и обозначается 1, число (0,1) называется мнимой единицей и обозначается i. Комплексные числа (a,b) можно обозначать в виде a+ib. При таких обозначениях арифметические операции над комплексными числами выполняются по обычным алгебраическим правилам, но при этом i2 заменяется на -1. Число a-ib называется комплексно сопряжённым к числу a+ib.
Модулем комплексного
числа u=a+ib
называется
действительное число
![]() .
При этом можно записатьu=|u|(cosj+isinj)
(тригонометрическая форма записи), где
j
- некоторый угол из промежутка [0;2p)
называемый
аргументом числа u.
Справедливы свойства:
.
При этом можно записатьu=|u|(cosj+isinj)
(тригонометрическая форма записи), где
j
- некоторый угол из промежутка [0;2p)
называемый
аргументом числа u.
Справедливы свойства:
|u|³0
|-u|=|u|
|uv|=|u||v|
|u+v|£|u|+|v| (неравенство треугольника для модуля)
|u-v|³|u|-|v| (следствие из неравенства треугольника)
un=|u|n(cosnj+isinnj) (формула возведения в степень)
![]() (формула
извлечения корня n-ой
степени)
(формула
извлечения корня n-ой
степени)
Для вычисления
квадратного
корня
кроме общего способа можно использовать
специальный приём.
Пусть
требуется вычислить квадратный корень
из числа a+ib.
Обозначим
этот корень через x+iy.
По
определению квадратного корня a+ib
= (x+iy)2.
Раскрывая
скобки и сравнивая получаем систему
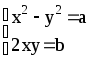
Её решения дадут нам два значения квадратного корня.
Пример 1.
(1+i)(5-i)=5+5i-i-i2=5+5i-i+1=6+4i (i2 заменили на -1)
Ответ: 6+4i
Пример 2.
![]() (домножили
числитель и знаменатель на 1-i
(сопряжённое
к 1+i)
и затем i2
заменили
на -1)
(домножили
числитель и знаменатель на 1-i
(сопряжённое
к 1+i)
и затем i2
заменили
на -1)
Ответ: 1+i
Пример 3.
(1-i)5
=
(![]() (cos(7p/4)+isin(7p/4))5
=
4
(cos(7p/4)+isin(7p/4))5
=
4![]() (cos(35p/4)+isin(35p/4))
=
(cos(35p/4)+isin(35p/4))
=
=
4![]() (-
(-![]() /2+i
/2+i![]() /2)
= -4+4i (перешли
к тригонометрической форме записи и
воспользовались формулой возведения
в степень)
/2)
= -4+4i (перешли
к тригонометрической форме записи и
воспользовались формулой возведения
в степень)
Ответ: -4+4i
Пример 4.
Вычислить
![]() .
Решение:
.
Решение: ![]() ,обозначим
значения корня (их четыре) через u0,
u1,
u2,
u3.
По
формуле извлечения корня
,обозначим
значения корня (их четыре) через u0,
u1,
u2,
u3.
По
формуле извлечения корня
![]() .
.
При к=0 получаем u0=cos(p/8)+isin(p/8)
При к=1 получаем u1=cos(5p/8)+isin(5p/8)
При к=2 получаем u2=cos(9p/8)+isin(9p/8)
При к=3 получаем u3=cos(13p/8)+isin(13p/8)
Ответ: { cos(p/8)+isin(p/8); cos(5p/8)+isin(5p/8); cos(9p/8)+isin(9p/8); cos(13p/8)+isin(13p/8) }
Пример 5.
Вычислить
![]() .
.
Составим систему
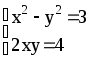 Û
Û
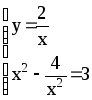 Þ
x4-3x2-4=0.
Þ
x4-3x2-4=0.
Обозначим t=x2 Þ t2-3t-4=0 Þ t1=-1, t2=4 Þ x2=4 Þ x1=-2, y1=-1 и x2=2, y2=1
Ответ: { -2-i; 2+i }
Пример 6.
Решить уравнение
x2
+ 4x + 5 = 0. Находим
D
= 16 - 4×5
= -4 < 0 Þ
корни
комплексные:
![]()
Ответ: { -2-i ; -2+i }
666
Вычислить:
1. (1+2i)(2+i) 2.
(1+2i):(2+i) 3.
![]()
4.
![]() 5.
5.![]()
Решить уравнения:
6. x2 - 16x + 65 = 0 7. 9x2 + 6x + 5 = 0
8. x4 + 2x2 - 3 = 0 9. x4 + 6x2 + 25 = 0
Вычислить:
10. (2+i)(3-i) 11.
(4+2i):(3-i) 12.
![]()
13.
![]()
Решить уравнения:
14. x2 + 12x + 40 = 0 15. x4 - 4x2 - 5 = 0
16. x4 - 6x2 + 25 = 0
555 Решение алгебраических уравнений.
Поиск рациональных корней алгебраических уравнений с целыми коэффициентами основан на теореме: если рациональное число - корень такого уравнения, то его числитель - множитель свободного члена, а знаменатель - множитель коэффициента при старшей степени. Для подстановки чисел в уравнение можно применять схему Горнера. В комплексной области любое алгебраическое уравнение n-ой степени имеет ровно n корней.
Схема Горнера.
Вычисления по схеме Горнера заносим в таблицу из двух строк. Слева от таблицы пишем проверяемое число. В первой строке записываем коэффициенты исходного уравнения, включая нулевые. Затем в первую ячейку второй строки переписываем число из верхней ячейки, во вторую ячейку второй строки записываем сумму верхнего числа и предыдущего, умноженного на проверяемое число и т.д. Если в последней ячейке получится 0, то проверяемое число - корень, а остальные числа - коэффициенты алгебраического уравнения с уменьшенной на один степенью. Решая это уравнение получим остальные корни.
Пример 7.
Решить уравнение x3 + x - 2 = 0. Рациональные корни этого уравнения ищем среди чисел ±1, ±2. Проверяем число 1:
|
1 |
1 |
0 |
1 |
-2 |
|
|
1 |
1 |
2 |
0 |
Так как в последней
ячейке ноль, то x1=1.
Остальные
корни ищем из уравнения x2
+ x + 2 = 0
(его коэффициенты берём из второй
строки).
D = 1 - 8 = - 7 < 0 Þ
![]()
Ответ:
![]()
666
Решить уравнения:
17. x3 - x2 - 2x + 2 = 0 18. x3 + x2 - 2 = 0
19. x5 - 4x3 - 8x2 + 32 = 0 20. x3 - 12x2 + 47x -60 = 0
21. x4 - 10x3 + 35x2 - 50x + 24 = 0
555
|
Выучить наизусть |
|
|u+v|£|u|+|v| |u-v|³|u|-|v| u=|u|(cosj+isinj) un=|u|n(cosnj+isinnj)
|
Ответы.
1. 5i 2. 0,8+0,6i 3. 3+i; -3-i
4. 2(cos(p/10+2kp/5)+isin(p/10+2kp/5)), k=0,1,2,3,4
5. Ö2(cos(p/36+2kp/3)+isin(p/36+2kp/3)), k=0,1,2 6. 8±i 7. -1/3±2i/3
8. ±1; ±iÖ3 9. 1±2i; -1±2i 10. 7+i 11. 1+i 12. ±(3-i)
13. 2(cos(3p/8+kp/2)+isin(3p/8+kp/2)), k=0,1,2,3 14. -6±2i 15. ±i; ±Ö5 16. 2±i; -2±i 17. 1; ±Ö2 18. 1; -1±i 19. ±2; -1±iÖ3 20. 3; 4; 5 21. 1;2;3;4
Вычислить u+v,
u-v, uv,
![]() ,
,![]()
3.1 u=3-4i v=8+6i 3.2 u=21+20i v=9-40i
3.3 u=-16+30i v=-21-20i 3.4 u=-9-40i v=21-20i
3.5 u=24+10i v=-15+8i 3.6 u=-21+20i v=-8-6i
3.7 u=24-10i v=-21-20i 3.8 u=3+4i v=-5+12i
3.9 u=21-20i v=7+24i 3.10 u=-7+24i v=24-10i
3.11 u=-7+24i v=-16+30i 3.12 u=7+24i v=-5+12i
3.13 u=-7-24i v=5+12i 3.14 u=21-20i v=-16-30i
3.15 u=-16-30i v=16+30i 3.16 u=3-4i v=7-24i
3.17 u=16+30i v=-15+8i 3.18 u=-8-6i v=16-30i
3.19 u=24+10i v=8+6i 3.20 u=-3+4i v=7-24i
3.21 u=21+20i v=16+30i 3.22 u=5-12i v=9-40i
3.23 u=5-12i v=8+6i 3.24 u=-9+40i v=-16+30i
3.25 u=5-12i v=-7-24i 3.26 u=-16-30i v=21+20i
3.27 u=-16+30i v=15-8i 3.28 u=-7-24i v=-8-6i
3.29 u=21-20i v=-5-12i 3.30 u=-8-6i v=-15-8i
3.31 u=-16-30i v=-3+4i 3.32 u=7+24i v=-9+40i
3.33 u=-24-10i v=21-20i 3.34 u=-7-24i v=8+6i
3.35 u=15-8i v=8-6i
Возвести в степень, преобразовав в тригонометрическую форму и вычислить корень этой же степени:
4.1 (-Ö3+i)3 4.2 (-1+iÖ3)7 4.3 (-1+i)7
4.4 (1-iÖ3)5 4.5 (1+iÖ3)3 4.6 (Ö3-i)3
4.7 (Ö3+i)3 4.8 (-1+i)3 4.9 (-Ö3-i)3
4.10 (-Ö3+i)7 4.11 (-Ö3+i)3 4.12 (1-i)5
4.13 (1+iÖ3)5 4.14 (1-iÖ3)3 4.15 (1-iÖ3)7
4.16 (-Ö3-i)3 4.17 (-1+iÖ3)3 4.18 (-1+i)7
4.19 (1-i)7 4.20 (1-iÖ3)3 4.21 (1-i)3
4.22 (-1+iÖ3)5 4.23 (-1-i)5 4.24 (-Ö3-i)3
4.25 (Ö3-i)5 4.26 (1+i)7 4.27 (1-i)7
4.28 (-Ö3+i)3 4.29 (-1-i)7 4.30 (1+i)3
4.31 (-1+iÖ3)3 4.32 (-Ö3-i)3 4.33 (-1-iÖ3)5
4.34 (-1+i)5 4.35 (-1-iÖ3)7
Найти действительные и комплексные корни уравнений:
5.1 x4+10x3+37x2+58x+30=0 75x3-35x2-8x+4=0
5.2 x4-5x3-6x2+84x-144=0 12x3-68x2+115x-50=0
5.3 x4-9x3+30x2-52x+48=0 18x3-15x2-100x+125=0
5.4 x4-2x3-7x2+18x-18=0 18x3-33x2-28x-5=0
5.5 x4+8x3+22x2+28x+16=0 75x3-140x2+87x-18=0
5.6 x4-9x3+30x2-46x+24=0 12x3+40x2+39x+9=0
5.7 x4-9x3+25x2-9x-44=0 12x3+20x2+4x-4=0
5.8 x4+5x3+x2-3x+36=0 20x3+60x2+60x+20=0
5.9 x4-5x3-8x2+82x-120=0 20x3+76x2+64x-16=0
5.10 x4-7x3+16x2 - 24=0 75x3+40x2-33x-18=0
5.11 x4+7x3+11x2-25x-66=0 12x3-56x2+80x-32=0
5.12 x4-6x3+10x2+6x-11=0 12x3+4x2-5x-2=0
5.13 x4-3x3-11x2+13x+60=0 75x3+35x2-123x+45=0
5.14 x4-3x3-10x2+6x+72=0 45x3+57x2+23x+3=0
5.15 x4-3x3-8x2+22x-24=0 18x3+33x2-28x+5=0
5.16 x4-7x3+20x2-32x+24=0 12x3+8x2-20x-16=0
5.17 x4+5x3-2x2-42x-72=0 45x3+42x2-4x-8=0
5.18 x4-6x3+14x2-18x+9=0 12x3+32x2+23x+5=0
5.19 x4-11x3+46x2-90x+72=0 45x3-141x2+95x+25=0
5.20 x4+2x3-14x2-32x-32=0 20x3-104x2+145x-25=0
5.21 x4-10x3+37x2-62x+40=0 20x3-76x2+64x+16=0
5.22 x4-11x3+48x2-96x+72=0 50x3-85x2-92x-20=0
5.23 x4 - 3x2+14x-12=0 12x3-80x2+175x-125=0
5.24 x4+7x3+18x2+28x+16=0 12x3-76x2+155x-100=0
5.25 x4+2x3-10x2-44x-48=0 20x3+44x2+28x+4=0
5.26 x4+8x3+25x2+36x+18=0 20x3+68x2+69x+18=0
5.27 x4-7x3+16x2-18x+8=0 18x3+27x2 - 9=0
5.28 x4-5x3-2x2+42x-72=0 50x3+55x2-28x+3=0
5.29 x4-3x3-3x2+31x-42=0 18x3+60x2+56x+16=0
5.30 x4-4x3-8x2+72x-96=0 75x3+170x2+128x+32=0
5.31 x4 - 10x2-20x-16=0 75x3-20x2-17x-2=0
5.32 x4+13x3+66x2+156x+144=0 20x3+104x2+145x+25=0
5.33 x4-4x3 + 8x-32=0 50x3+110x2+78x+18=0
5.34 x4-8x3+23x2-34x+24=0 18x3-93x2+152x-80=0
5.35 x4-8x3+24x2-32x+15=0 20x3+44x2+28x+4=0
