3. Линейная алгебра. Матрицы и основные операции с ними.

Матрицей называется прямоугольная таблица чисел, например:

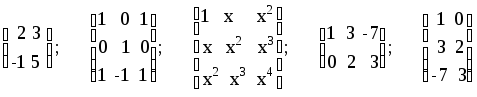
Сумма (разность) матриц одного порядка получается сложением (вычитанием) соответствующих элементов этих матриц.

Произведение матрицы на число получается умножением каждого элемента матрицы на это число.

Можно умножить две матрицы, если число столбцов первой матрицы равно числу строк второй. Элементы этой матрицы равны суммам произведений элементов строк первой матрицы на элементы столбцов второй матрицы.

Матрица называется квадратной, если число строк равно числу столбцов.

Квадратная матрица называется единичной, если диагональные элементы равны единице, а остальные - нулю.

Матрица называется обратной к квадратной, если её произведение на заданную равно единичной матрице.

Определители 2-го и 3-го порядка.

Для квадратной матрицы можно вычислить число, которое называется определителем. Определитель второго порядка вычисляется по схеме крест, а определитель третьего порядка - по схеме треугольников.

Схема крест (звёздочкой обозначены перемножаемые элементы):

~	×	_	×	~
×	~		~	×

Схема треугольников:

~

×

×

×

~

×

×

×

~

×

×

~

×

~

×

~

×

×

×

~

×

+

×

×

~

+

~

×

×

-

×

~

×

-

~

×

×

-

×

×

~

×

×

~

~

×

×

×

~

×

~

×

×

×

×

~

×

~

×

Правило разложения по первой строке (знак +, если сумма индексов чётна и -, если нечетна; аналогично записывается разложение по другим строкам и столбцам):

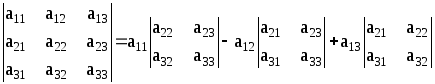
Пример 1.

= 1×7-4×3=-5

Пример 2.

1	2	4
3	5	-3	=(1×5×(-2)+2×(-3)×(-1)+3×6×4)-(4×5×(-1)+2×3×(-2)+(-3)×6×1)=118
-1	6	-2

Решение систем линейных уравнений с помощью определителей.

Пусть дана система двух уравнений с двумя неизвестными:

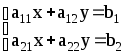
Для решения этой системы вычислим определители:

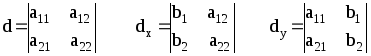
Если d¹0, то система имеет единственное решение: x=d_x/d, y=d_y/d. Если d=0, а dx¹0 или d_y¹0 то система не имеет решений. Если d=d_x=d_y=0, то одно из уравнений системы следствие другого. В этом случае его надо отбросить и решать оставшееся уравнение.

Пример 3.

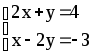
Вычисляем

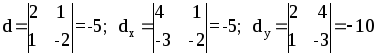
Так как d¹0, то находим x=-5:(-5)=1; y=-10:(-5)=2

Ответ: (1;2)

Рассмотрим теперь систему трёх уравнений с тремя неизвестными:

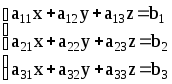
Для решения этой системы вычислим определители:

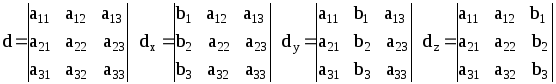
Если d¹0, то система имеет единственное решение: x=d_x/d, y=d_y/d, z=d_z/d. Если d=0, а d_x¹0 или d_y¹0 или d_z¹0, то система не имеет решений. Если d=d_x=d_y=d_z=0, то одно из уравнений системы следствие двух других. В этом случае его надо отбросить и решать систему оставшихся двух уравнений с тремя неизвестными.

Пример 4.

Вычисляем

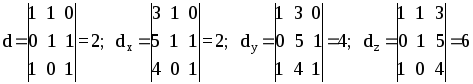
Так как d¹0, то находим x=2:2=1; y=4:2=2; z=6:2=3

Ответ: (1;2;3)

Если в правой части системы стоят нули, то система называется однородной. Если для такой системы d¹0, то она имеет единственное решение x=y=z=0. В противном случае одно уравнение следствие других. Выкинув его, получим однородную систему двух уравнений с тремя неизвестными:

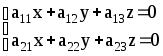
Для решения этой системы вычислим определители:

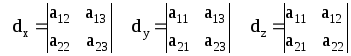
Система имеет бесконечно много решений: x=kd_x, y=-kd_y, z=kd_z, kÎR.

Пример 5.

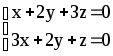
Вычисляем

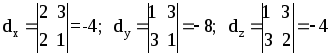
Следовательно x=-4k, y=8k, z=-4k, kÎR

Ответ: (-4k; 8k; -4k), kÎR

666

Решить системы:

1.		x + 3y = 10 3x - y = 0		2.				3x + y = 4 -x + 3y = 2
3.		x + 3y = 1 2x + 6y = 0		2.				9x + 3y = 1 3x + y = -1
5.		x - 3y = 1 2x - 6y = 2		6.				9x - 3y = 3 3x - y = -1
7.		2x - 3y + z = 2 x + 5y - 4z = -5 4x + y - 3z = -4		8.				2x - 4y + 3z = 1 x - 2y + 4z = 3 3x - y + 5z = 2
9.		x + 2y + 3z = 4 2x + 4y + 6z = 3 3x + y - z = 1			10.				x + 2y + 3z = 4 2x + y - z = 3 3x + 3y + 2z = 10
11.		x + 2y + 3z = 4 2x + y - z = 3 3x + 3y + 2z = 7			12.				x - 2y + z = 4 2x + 3y - z = 3 4x - y + z = 11
13.		-2x - y - z = 0 2x - 4y + 3z = 0 -5y + 2z = 0			14.				3x + 2z = 0 2x - 4y + 3z = 0 x + 4y - z = 0

555

Выучить наизусть

Схему крест. Схему треугольников. Правило разложения. Правила решения систем линейных уравнений с помощью определителей

Ответы.

1. (1; 3) 2. (1; 1) 3. Æ 4. Æ 5. (3k+1; k), kÎR 6. (k; 3k+1), kÎR

7. (5; 6; 10) 8. (-1; 0; 1) 9. Æ 10. Æ 11. ((2+5k)/3; (5-7k)/3; k), kÎR

12. (k; 7-3k; 18-7k), kÎR 13. (-7k; 4k; 10k), kÎR 14. (8k; -5k; -12k), kÎR