555 Приближенное решение уравнений.

Основные приближённые методы решения уравнений: метод итераций, метод деления пополам, метод хорд и метод касательных.

В методе итераций уравнение надо записать в виде x = f(x). Затем выбираем x₁, находим x₂ = f(x₁), x₃ = f(x₂) и т.д. Если |f¢(x)|<1, то последовательность x₁, x₂, x₃, ... сходится к корню уравнения. Процесс заканчивается, когда выполнится критерий окончания: |x_n-x_n-1|£(1/r-1)e, где r=max|f¢(x)| на промежутке на котором расположены числа x₁, x₂, x₃, ..., а e - заданная точность. Если разности x_n-x_n-1 знакочередующиеся, то процесс заканчивается, когда |x_n-x_n-1|£2e. Корнем в этом случае считается полусумма двух последних значений x. Вычисления удобно оформить в виде таблицы.

Пример 2.

Решить уравнение x³+x-1=0 с точностью 0,01. Перепишем уравнение в виде .Выберем x₁=0, получаем:

x	0	1	0,5	0,8	0,61	0,729	0,653	0,701	0,671	0,690
	1	0,5	0,8	0,61	0,729	0,653	0,701	0,671	0,690

Так как |0,690-0,671|<0,02, то процесс закончен и x»(0,690+0,671):2»0,680. Обратите внимание на то, что вычисления делаются с одним запасным знаком после запятой.

В методе деления пополам уравнение записывается в виде f(x)=0, затем выбирается отрезок [a₁;b₁], на концах которого функция f(x) имеет разные знаки. Этот отрезок делится пополам и через [a₂;b₂] обозначается та половина, на концах которой функция f(x) имеет разные знаки и т. д. Процесс деления заканчивается, когда длина очередного отрезка станет меньше удвоенной точности. Корнем считается середина последнего отрезка. Вычисления удобно оформить в виде таблицы.

Пример 3.

Решить уравнение x³+x-1=0 с точностью 0,01.

x	x3+x-1	[a;b]
0	-1
1	1	[0;1]
0,5	-0,375	[0,5;1]
0,75	0,172	[0,5;0,75]
0,625	-0,131	[0,625;0,75]
0,688	0,014	[0,625;0,688]
0,657	-0,059	[0,657;0,688]
0,673	0,022	[0,673;0,688]

Так как |0,688-0,673|<0,02, то процесс закончен и x»(0,688+0,673):2»0,680. Обратите внимание на то, что вычисления делаются с одним запасным знаком после запятой.

В методе хорд уравнение записывается в виде f(x)=0, затем выбирается отрезок [a₁;b₁], на концах которого функция f(x) имеет разные знаки. Если f(a₁)f²(a₁) < 0 то вычисления проводим по формулам:

a₂=a₁-f(a₁), a₃=a₂-f(a₂), и т.д.

Вычисления заканчиваем, когда |a_n-a_n-1|<e. Корнем считается последнее вычисленное значение a_n. Если f(b₁)f²(b₁) < 0 то вычисления проводим по формулам:

b₂=b₁-f(b₁), b₃=b₂-f(b₂), и т.д.

Вычисления заканчиваем, когда |b_n-b_n-1|<e. Корнем считается последнее вычисленное значение b_n. Вычисления удобно оформить в виде таблицы.

В методе касательных уравнение записывается в виде f(x)=0, затем выбирается отрезок [a₁;b₁], на концах которого функция f(x) имеет разные знаки. Если f(a₁)f²(a₁) > 0 то вычисления проводим по формулам:

a₂=a₁-, a₃=a₂-, и т.д.

Вычисления заканчиваем, когда |a_n-a_n-1|<e. Корнем считается последнее вычисленное значение a_n. Если f(b₁)f²(b₁) < 0 то вычисления проводим по формулам:

b₂=b₁-, b₃=b₂-, и т.д.

Вычисления заканчиваем, когда |b_n-b_n-1|<e. Корнем считается последнее вычисленное значение b_n. Вычисления удобно оформить в виде таблицы.

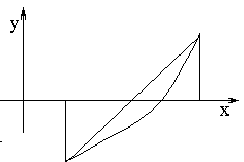
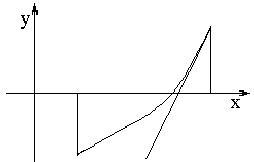
Метод хорд и метод касательных обычно применяются совместно.

Метод хорд
Метод касательных

Пример 4.

Решить уравнение x³+x-1=0 с точностью 0,0001. Обозначим f(x)= x³+x-1. Так как f(0)=-1<0 и f(1)=1>0, то исходный отрезок [0;1]. Слева применим метод хорд (так как f(0)f²(0)<0), а справа - метод касательных (так как f(1)f²(1)>0).

a	b	f(a)	f(b)	f¢(b)
0	1	-1	1	4
0,5	0,75	-0,375	0,17188	2,6875
0,67143	0,68604	-0,02588	0,00893	2,41195
0,68229	0,68234

Так как |0,68234-0,68229|<0,0002, то процесс закончен и x»(0,68229+0,68234):2»0,68231. Обратите внимание на то, что вычисления делаются с одним запасным знаком после запятой.

666

Решить с точностью до 0,001:

29. x = 1 + lnx 30. x³ - cosx = 0

31. x³+100x=1000 32. x⁵ + 10x³ + 1 = 0

555

Выучить наизусть

Определение производной. Правила дифференцирования. Таблицу производных. Правила поиска экстремумов и перегибов. Формулы для приближённого решения уравнений.

Ответы.

18. 0,5 19. -0,5 21. y_min=ln6 при x=0 22. y_min=-3 при x=(2k+1)p, y_max=5 при x=2kp, kÎZ 23. при x=±1 24. При x=3±

29. 0,1586; 3,1462 30. 0,8655 31. 6,823 32. -0,4609