
515_Teorija Ehlektricheskikh Tsepej
.pdf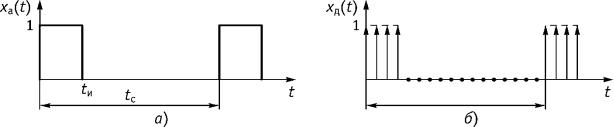
дискретизации удовлетворяет условию д 2 в; в этом случае аналоговый сигнал можно восстановить, зная спектр дискретизированного сигнала, если применить ФНЧ с комплексной передаточной функцией Hф j и частотой среза (частотой пропускания), равной с 0,5 д.
Прямое и обратное дискретное преобразование Фурье периодических дискретных сигналов
Пусть имеется аналоговый сигнал x(t) в виде периодической последовательности импульсов, длительность импульсов tимп = 4 мс, период следования импульсов Tс = 16 мс, амплитуда импульса Um = 1 В (рис. 9.6 а).
Рис. 9.6
Произведем дискретизацию периодического аналогового сигнала с периодом T = 1 мс, получим дискретный сигнал, приведенный на рис. 9.6 б.
Запишем дискретный сигнал математически, используя -функцию. В качестве последовательности можно брать фрагмент любой величины, например, равный периоду аналогового сигнала Tс NT (N Tс /Т 16)
N 1 |
|
xд t x nT t nT . |
(9.11) |
n 0
В силу периодичности аналогового сигнала, спектр дискретизированного сигнала – дискретный, а так как аналоговый сигнал дискретизирован, то спектр дискретизированного сигнала – периодический в частотной области с периодом
2 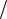 T .
T .
Итак, дискретизированный периодический сигнал имеет периодический дискретный спектр.
Прямое дискретное преобразование Фурье
N 1 |
j |
2 |
kn |
|
|
(9.12) |
|||
X k x nT e |
|
N . |
||
n 0
Обратное дискретное преобразование Фурье
|
1 |
N 1 |
j |
2 |
kn |
|
|
|
|
|
|||||
x nT |
X k e |
|
N . |
(9.13) |
|||
|
|||||||
|
N k 0 |
|
|
|
|
||
Замечание. ДПФ применим только к периодическому дискретному сигналу.
131
Теоремы (свойства) ДПФ
1. Теорема линейности
Пусть |
последовательности |
|
x |
|
nT и x |
2 |
nT имеют равные |
периоды и |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||
имеют ДПФ |
x nT |
X |
1 |
k , |
|
x |
2 |
nT X |
2 |
k , тогда |
|
|
|
||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
a x |
nT a |
2 |
x |
2 |
nT a X |
1 |
k a |
2 |
X |
2 |
k . |
(9.14) |
||||||||
|
1 |
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||
2. Теорема задержки (сдвига) последовательности |
|
|
|||||||||||||||||||
если x n X k , тогда x m x n n |
|
X k exp( j |
2 |
kn |
|
), (9.15) |
||||||||
|
|
|
||||||||||||
1 |
|
|
|
0 |
|
N |
0 |
|
||||||
где n0 – задержка последовательности. |
|
|
|
|
|
|
|
|||||||
3. Свойство симметрии |
|
|
|
|
|
|
|
|||||||
|
X р k |
|
|
|
X р N k |
|
, |
где N – период. |
|
(9.16) |
||||
|
|
|
|
|
||||||||||
4. Свойство периодичности
ДПФ является периодической функцией частоты, с периодом, равным N
(в нормированном виде), или с периодом, равным д |
|
д N2 /Tс , |
(9.17) |
где Tс – период аналогового сигнала.
5. Свойство произведения двух периодических последовательностей:
произведение двух периодических последовательностей соответствует круговой свертке ДПФ этих последовательностей
|
1 |
N 1 |
|
|
|
|
|
|
|
||
x1 |
n x2 n |
|
X1 i X 2 k i mod N . |
(9.18) |
|||||||
|
|||||||||||
|
|
N i 0 |
|
|
|
|
|
|
|
||
6. Равенство Парсеваля |
|
|
N 1 |
|
|
|
|
|
|
||
|
|
1 |
|
|
|
2 |
|
|
|||
|
|
|
|
|
|||||||
|
x2 n |
|
|
|
X k |
|
|
. |
(9.19) |
||
|
|
|
|
||||||||
|
n 0 |
|
N k 0 |
|
|
|
|
|
|
||
7. Теорема круговой свертки периодических последовательностей
Круговой свертке периодических последовательностей соответствует произведение ДПФ последовательностей
x n x |
2 |
n X |
1 |
k X |
2 |
k , |
(9.20) |
1 |
|
|
|
|
где – знак круговой свертки.
Замечание 1. Следует иметь в виду, что круговая свертка последовательностей берется на периоде N.
Замечание 2. Круговую свертку двух периодических последовательностей не следует путать с линейной дискретной сверткой двух последовательностей, которая является основой алгоритма дискретной фильтрации.
Z-преобразование дискретных сигналов
Z-преобразование в цифровой обработке сигналов играет такую же роль, как и преобразование Лапласа при анализе аналоговых цепей и сигналов.
132
Z-преобразование применяется к непериодическим последовательностям. При z-преобразовании последовательности x(n) ставится в соответствие функция комплексной переменной z
X z |
|
|
||
x n z n , |
(9.21) |
|||
|
|
n |
|
|
где z = epT. |
|
|
|
|
Условие сходимости z-преобразования сигнала x n |
|
|||
|
|
|
|
|
|
|
|
|
|
|
x n z n |
. |
(9.22) |
|
|
n |
|
|
|
Область сходимости z-преобразования сигнала x n : те значения z, при которых выполняется условие сходимости.
Основные теоремы (свойства) z-преобразования
1. Свойство однозначности: каждой последовательности x(n) соответствует одно и только одно z-преобразование.
2. Свойство |
линейности: |
|
если |
|
сигналы |
|
x |
|
n |
|
и |
|
x |
2 |
n имеют z- |
||||||||||||||||||||
преобразования |
X1 z и X2 z , тогда |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
z a |
|
|
|
z . |
|
|
|
||||||||||||||||||||||
|
a |
1 |
x |
nT a |
2 |
x |
2 |
nT |
a |
1 |
X |
1 |
2 |
X |
2 |
|
|
(9.23) |
|||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3. Свойство задержки |
(сдвига): если x n X z , тогда |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x n m X z z m. |
|
|
|
|
|
|
|
|
|
|
|
|
(9.24) |
||||||||||||||||
4. Теорема |
свертки: |
свертка |
сигналов |
|
x |
|
|
n |
x |
2 |
n |
соответствует |
|||||||||||||||||||||||
умножению z-преобразований сигналов |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
x n x |
2 |
n X |
1 |
z |
X |
2 |
z . |
|
|
|
|
|
|
(9.25) |
|||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5. Теорема умножения сигналов: умножение сигналов соответствует |
|||||||||||||||||||||||||||||||||||
свертке z-преобразований сигналов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
x |
n x |
|
n |
1 |
|
|
X |
|
v X |
|
|
z |
v 1dv, |
|
|
|
(9.26) |
||||||||||||||||
|
|
2 |
2 j |
1 |
2 |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где z и v – комплексные переменные на комплексной плоскости z.
6. Теорема Парсеваля
|
1 |
X z X z 1 z 1dz, |
|
|
x2 n |
(9.27) |
|||
|
||||
n |
2 j |
c |
|
где С – контур интегрирования.
7. Теорема опережающего сдвига
x n 1 z X z x 0 . |
(9.28) |
8. Обратное z-преобразование
x n |
1 |
X z zn 1dz. |
(9.29) |
|
2 j |
||||
|
c |
|
||
|
|
|
133
Методы определения сигнала по его z-изображению
1. Метод, основанный на определении обратного преобразования с помощью теоремы вычетов
x n |
1 |
c |
X z zn 1dz |
1 |
c |
F z dz ResF z . |
(9.30) |
|
2 j |
2 j |
|||||||
|
|
zn |
|
2.Метод разложения функции X z на простые дроби.
3.Метод непрерывного деления полинома числителя на полином знаменателя.
4.Метод разложения z-преобразования в степенной ряд (ряд Тейлора).
Преобразование точек р плоскости в точки z-плоскости
Преобразование точек р плоскости в точки z-плоскости производится по формуле z re j epT , при этом все точки полосы от j0,5 д до j0,5 д в
плоскости р переходят во всю плоскость z (рис. 9.7).
Рис. 9.7
Это приводит к эффекту наложения и к ошибкам при проектировании цифровых фильтров по аналоговому прототипу. Поэтому преобразование вида z e j T re j непосредственно не используется при проектировании цифровых фильтров по аналоговому прототипу.
134
Лекция 17 Дискретные цепи
Дискретная цепь – любая система (цепь), преобразующая одну последовательность х(n) в другую последовательность y(n).
Свойство линейности дискретной цепи – выходная реакция на сумму дискретных сигналов равна сумме реакций на эти сигналы.
Свойство стационарности дискретной цепи – задержка входного дис-
кретного сигнала приводит лишь к такой же задержке выходного дискретного сигнала.
Методы анализа дискретных цепей
1.Метод разностных уравнений.
2.Метод z-преобразований.
3.Дискретная свертка (линейная, круговая).
4.Спектральный метод.
5.Метод пространства состояния.
Разностные уравнения дискретных цепей
Разностные уравнения можно получить на основе дифференциального уравнения э/цепи, заменяя 1-ю производную dx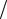 dt первой разностью nT
dt первой разностью nT
|
|
|
nT |
x nT x nT T |
|
|||
|
|
|
|
, |
(9.31) |
|||
|
|
|
|
|||||
|
|
|
|
|
|
T |
|
|
вторую производную d 2x |
dt2 – второй разностью 2 nT |
|
||||||
2 |
nT |
nT nT T |
|
x nT 2x nT T x nT 2T |
и т.д. (9.32) |
|||
T |
|
|
T 2 |
|||||
|
|
|
|
|
|
|||
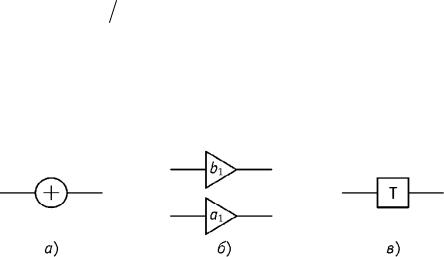
Дискретные цепи в общем случае имеют элементы: сумматоры (рис. 9.8 а), умножители (рис. 9.8 б) и устройство задержки (рис. 9.8 в).
Рис. 9.8
Рекурсивные и нерекурсивные дискретные цепи
1. Если разностное уравнение имеет как прямые, так и обратные связи
M L
y nT amx nT mT bl y nT lT , m 0 l 1
прямая связь |
обратная связь |
то ему соответствует рекурсивная дискретная цепь, представленная на рис. 9.9 а.
135
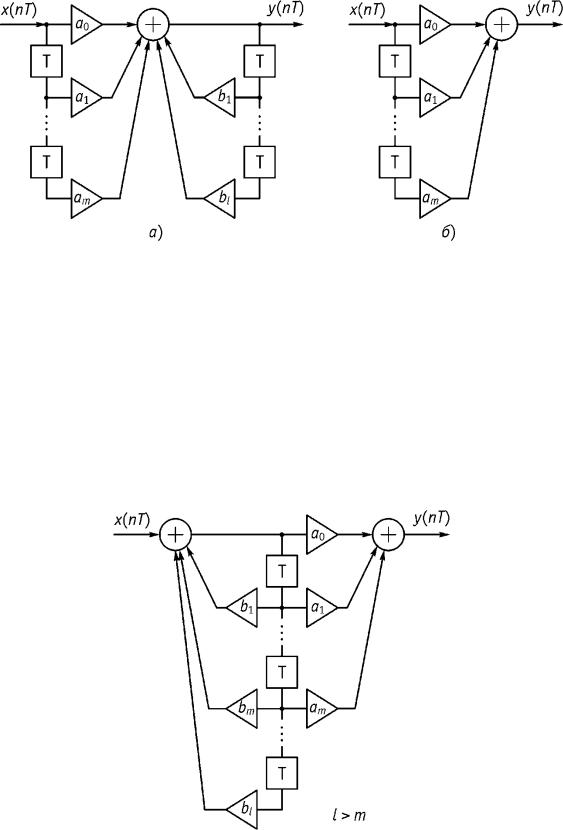
Рис. 9.9
2. Если разностное уравнение имеет только прямые связи
M |
|
y nT amx nT mT , |
(9.33) |
m 0
то ему соответствует нерекурсивная цепь (рис. 9.9 б).
Формы реализации дискретной цепи на основе разностного уравнения
1.Прямая форма (рис. 9.9 а, б).
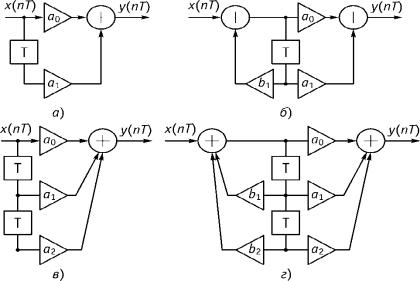
2.Каноническая форма (рис. 9.10).
3.Транспонированная форма.
Рис. 9.10
Передаточные функции дискретной цепи
Передаточная функция дискретной цепи есть отношение z-преобра-
зования Y(z) выходного сигнала к z-преобразованию X(z) входного сигнала.
136
Передаточная функция рекурсивной цепи имеет вид
|
|
|
M |
|
|
|
H z |
Y z |
|
amz m |
|
|
|
|
m 0 |
|
. |
(9.34) |
||
X z |
L |
l |
||||
|
1 blz |
|
|
|||
|
|
|
|
|
||
l 1
Передаточная функция нерекурсивной цепи имеет вид
|
Y z |
M |
|
|
H z |
|
amz m . |
(9.35) |
|
X z |
||||
|
m 0 |
|
Поскольку передаточная функция H(z) рекурсивной цепи в общем случае есть отношение полиномов, то передаточную функцию можно записать, используя нули и полюсы функции H z
|
|
|
|
H z H |
|
1 z10z |
1 1 zM0z 1 |
, |
(9.36) |
|||||||||||
|
|
|
|
0 |
1 |
|
z1z |
1 |
|
|
1 |
|
zLz |
1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где |
H0 – |
некоторый коэффициент; |
z10, ,zM0 |
– нули, z1, ,zL |
– полюсы |
|||||||||||||||
функции H(z). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Передаточную функцию H(z) можно представить также в виде суммы про- |
|||||||||||||||||||
стых дробей (можно разложить на простые дроби) |
|
|
|
|||||||||||||||||
H z |
r1 |
|
r2 |
|
|
|
rL |
|
k |
0 |
k1z 1 k(M L)z(M L), (9.37) |
|||||||||
1 z1z 1 |
1 z2z 1 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
1 zLz 1 |
|
|
|
|
|
|
|
|
|
||||||
где |
r1, r2, ,rL |
– |
вычеты |
функции |
H(z) |
|
|
в |
соответствующих |
полюсах; |
||||||||||
k0, ,kM L – коэффициенты, представляющие целую часть функции передачи
H(z).
Звенья дискретных фильтров
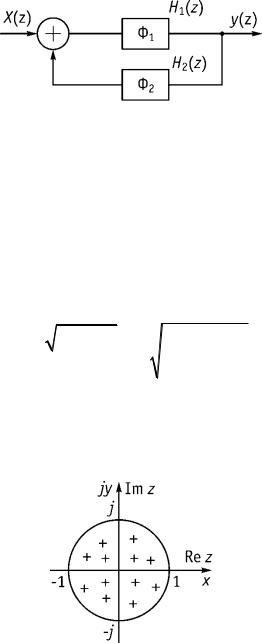
1.Звено 1-го порядка: нерекурсивной цепи (рис. 9.11 а), рекурсивной цепи
(рис. 9.11 б).
2.Звено 2-го порядка: нерекурсивной цепи (рис. 9.11 в), рекурсивной цепи
(рис. 9.11 г).
Рис. 9.11
137
Виды соединения дискретных фильтров (или звеньев фильтров)
1. Каскадное соединение
Передаточная функция каскадного соединения фильтров имеет вид
|
H |
|
z |
|
H1 |
|
z |
|
|
Hk |
|
z |
. |
(9.38) |
||
|
|
|
|
|
|
|
|
|
||||||||
2. |
Параллельное соединение звеньев фильтров |
|
||||||||||||||
|
H z H1 z H2 z Hk z . |
(9.39) |
||||||||||||||
3. |
Включение фильтра (Ф2) |
|
в обратную цепь другого фильтра (Ф1) |
|||||||||||||
(рис. 9.12) |
|
|
|
|
|
|
|
H1 z |
|
|
|
|
|
|||
|
H z |
|
|
|
|
|
|
|
. |
(9.40) |
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
1 H1 z H2 z |
|
||||||||||
Рис. 9.12
Добротность полюсов передаточной функции Н(z)
Пусть i-ый полюс передаточной функции равен
z |
i |
epiT |
e iTe j iT |
r e j i . |
(9.41) |
|
|
|
i |
|
Прологарифмируем данное выражение, получим
iT j iT lnri j i . |
(9.42) |
Из полученного соотношения определяем добротность i-го полюса (Т=1)
Q |
i2 i2 |
|
1 |
1 |
|
i |
2 . |
(9.43) |
|
|
|
lnr |
|||||||
i |
2 |
i |
2 |
|
|
|
|||
|
|
|
|
|
|
i |
|
||
Условие устойчивости дискретной цепи
Дискретная цепь устойчива, если полюсы zi находятся внутри круга единичного радиуса на комплексной плоскости z (рис. 9.13).
Рис. 9.13
138

Условия реализуемости вещественного дискретного фильтра по передаточной функции H(z)
1.Полюсы передаточной функции должны находиться внутри круга единичного радиуса на комплексной плоскости Z.
2.Коэффициенты аi и bj передаточной функции H(z) должны быть действительными числами.
Комплексная частотная характеристика дискретной цепи
Комплексная частотная характеристика дискретной цепи есть отно-
шение преобразования Фурье выходного сигнала к преобразованию Фурье входного сигнала
|
|
|
|
|
|
M |
|
|
|
H e j T |
Y e j T |
H z |
|
|
|
ame jm T |
|
||
|
z e j T |
|
m 0 |
|
. |
(9.44) |
|||
|
|
||||||||
X e j T |
|
L |
|
||||||
|
|||||||||
|
|
|
|
|
jl T |
|
|||
|
|
|
|
|
1 ble |
|
|
|
|
|
|
|
|
|
|
l 1 |
|
|
|
Частотная характеристика H(e j T ) совпадает с передаточной функцией |
Н(z) |
||||||||
на единичной окружности z-плоскости, поскольку существует связь между z- преобразованием последовательности и преобразованием Фурье этой последовательности H z z e j T H e j T .
Основные свойства частотной характеристики
1.Частотные характеристики дискретных цепей являются непрерывными функциями частоты.
2.Частотные характеристики дискретных цепей являются периодическими функциями в частотной области с периодом, равным частоте дискретизации
д 2 /Т .
3.Для вещественных фильтров, передаточные функции которых имеют только
вещественные коэффициенты ai,bj амплитудно-частотная характеристика H ej T и групповое время прохождения ( ) д argH(e j T ) /д – чет-
ные функции частоты, а фазо-частотная функция ( ) arg H ej T – нечетная функция частоты .
Импульсная характеристика дискретной цепи
Импульсная характеристика дискретной цепи h(nT) есть реакция дискретной цепи на единичную импульсную функцию.
Импульсная характеристика h(nT) и комплексная частотная характеристика H e j T связаны между собой парой преобразований Фурье
h nT |
1 |
|
H e j T e j nTd T , |
|
|
|
(9.45) |
||||
2 |
|||||
|
|
|
|
||
|
|
|
|
|
|
H e j T h nT e j nT . |
(9.46) |
||||
n 0
139

Устойчивость дискретной цепи во временной области
Дискретная цепь называется устойчивой, если при любых начальных условиях реакция y(nT) цепи на любое ограниченное воздействие x(nT) также ограничена.
Следовательно, необходимым и достаточным условием устойчивости дискретного фильтра во временной области является абсолютная сходимость ряда отсчетов импульсной характеристики
|
|
h nT . |
(9.47) |
n 0
Импульсная характеристика и передаточная функция дискретной цепи связаны парой z-преобразования.
|
|
|
|
|
|
H z h nT z n , |
(9.48) |
||||
|
n 0 |
|
|
|
|
h nT |
1 |
|
|
H z zn 1dz. |
(9.49) |
2 j |
|
||||
|
|
|
c |
|
|
Методы определения импульсной характеристики по передаточной функции дискретной цепи
1. Метод, основанный на определении обратного преобразования с помощью теоремы вычетов
h n |
1 |
c |
H z zn 1dz |
1 |
c |
F z dz ResF z . |
(9.50) |
|
2 j |
2 j |
|||||||
|
|
zn |
|
2.Метод разложения функции H z на простые дроби с последующим вычислением суммы интегралов от простых дробей.
3.Метод непрерывного деления полинома числителя на полином знаменателя функции H z ; позволяет получить только отсчеты импульсной характеристики.
4.Метод разложения z-преобразования в степенной ряд (ряд Тейлора); позволяет получить только отсчеты импульсной характеристики.
Метод линейной дискретной свертки
Следует заметить, что в большинстве случаев необходимым результатом на выходе системы цифровой обработки сигналов является аналоговый сигнал или выходная последовательность во временной области, которая определяется по формуле линейной дискретной свертки, поэтому линейная дискретная свертка является основой алгоритма цифровой фильтрации.
Постановка задачи: известны входной сигнал x(nT) , количество отсчетов сигнала N1 и импульсная характеристика цепи h(nT), количество отсчетов импульсной характеристики N2 . Необходимо найти выходной сигнал.
140
