
515_Teorija Ehlektricheskikh Tsepej
.pdf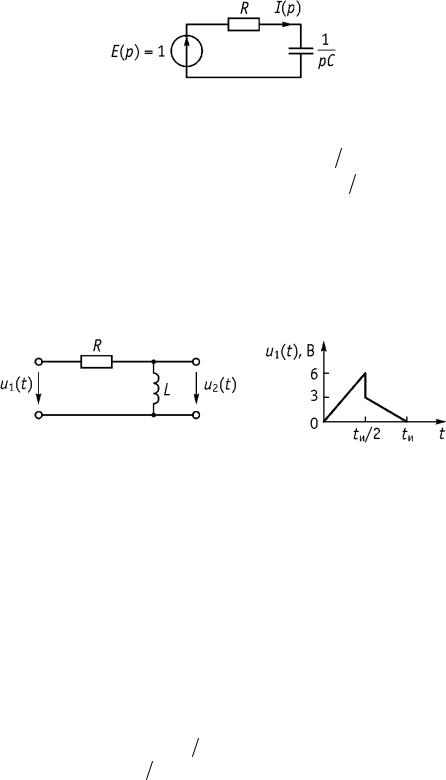
|
|
|
|
|
|
Рис. 7.7 |
|
|
|
|
|
|
|
|||
uC p I p |
1 |
|
pC |
|
1 |
|
1 |
|
|
1 |
RC |
10 |
3 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
pC |
pCR 1 |
pC |
pCR 1 |
|
|
p 103 |
||||||||||
|
|
|
|
|
p 1 RC |
|
||||||||||
Hu p uC p , тогда, перейдя от изображения к оригиналу, получим hu t 103e 103t , (1/с).
Пример 3. Задан сигнал u1(t) на входе электрической цепи (рис. 7.8). Найти закон изменения напряжения на выходе цепи методом интеграла Дюамеля.
R = 20 Ом, L = 50 мГн, tи = 20 мс.
Рис. 7.8
Решение
1. Определим переходную характеристику цепи gu(t). gu t guпр gu 0 guпр ept ,
gu 0 0, guпр 0,
p |
R |
|
20 |
400 |
c 1, |
|
50 10 3 |
||||
|
L |
|
|
||
gu t e 400t .
2. Опишем входной сигнал.
Для интервала времени t [0; ) его можно разбить на 3 участка
u11 t , |
0 t tи 2 |
|
600t, 0 t 10 мс |
||||
|
t , |
|
|
300t 6, 10 мс t 20 мс |
|||
u1 t u12 |
tи 2 t tи |
||||||
|
|
t |
|
, |
tи t |
|
0, t 20 мс. |
u13 |
|
|
|
||||
3. Запишем интеграл Дюамеля для определения u2(t). Для каждого из 3-х участков мы запишем свою формулу. I. 0 t tи/2.
t |
t |
u21 t u11 0 gu t u11 gu t d 600e 400 t d 1,5 1 e 400t В.
0 |
0 |
II. tи/2 t < tи.
111

tи 2
2
u22 |
|
t |
|
u11 |
|
0 |
|
gu |
|
t |
|
|
|
|
|
|
gu |
|
t |
|
d |
|
|
|
|
|
|
u11 |
|
|
|
|
102
0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
u1 |
|
tи |
|
|
|
|
tи |
|
|
|
t |
|
|
|
|
gu |
|
t |
|
d |
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
gu t |
|
|
|
u12 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
2 |
|
tи |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
t |
|
d 3e 400 |
|
t 10 |
3 |
|
|
|
t |
300e 400 |
|
t |
|
d 0,75 42,56e |
400t В. |
|||||||||||
600e 400 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
10 2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
III. t tи.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tи |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
u23 |
t |
|
|
|
|
0 |
gu |
t |
|
|
|
|
|
gu |
t |
d |
|
|
|||||||||||||||||||||
|
|
|
|
u11 |
|
|
|
|
|
u11 |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
и |
|
|
|
|
|
|
t |
и |
|
|
|
|
tи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
u1 |
2 |
|
gu t |
2 |
|
|
|
|
u12 |
|
|
|
gu |
|
|
t |
|
d |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tи |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
u1 tи gu t tи |
|
t |
|
|
|
gu |
|
t |
|
|
d |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
u13 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
10 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tи |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
400 t |
d 3e |
400 t 10 3 |
|
|
210 |
|
|
|
|
|
400 t |
d 2111,3e |
400t |
В. |
||||||||||||||||||||||||||
600e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
300e |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Получим (рис. 7.9) |
|
1,5 1 e 400t |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
0 t 10 2 с |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 2 t 2 10 2 с |
|
|
|||||||||||||||
|
|
u2 t 0,75 42,56e 400t, |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2111,3e |
|
400t |
, |
t 2 10 |
2 |
с. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Рис. 7.9
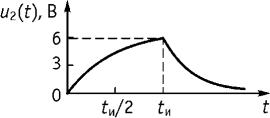
Пример 4. Задан сигнал u1(t) на входе электрической цепи (рис. 7.10). Найти закон изменения напряжения на выходе цепи методом интеграла свертки.
R = 20 Ом, L = 50 мГн, tи = 20 мс.
Рис. 7.10
112
Решение 1. Найдем импульсную характеристику цепи.
Переходная характеристика цепи по напряжению gu t guпр gu 0 guпр ept ,
gu 0 0, guпр 1,
p |
R |
|
20 |
|
400 |
c 1, |
|
50 10 3 |
|||||
|
L |
|
|
|||
|
gu t 1 1e 400t . |
|
||||
gu(0) = 0, тогда |
|
|
|
|
||
hu t gu t 400e 400t |
c 1. |
|||||
2. Опишем входной сигнал. |
|
|
|
|
||
u t , 0 t t |
|
6, 0 t 20 мс |
||||
u1 t u1211 t , t tи |
и |
0, t 20 мс. |
||||
3. Запишем интеграл свертки для определения u2(t). Для первого участка (0 t < tи):
t |
t |
u21 t u11 hu t d 6 400e 400 t d 6 1 e 400t В. 0 0
Для второго участка (t tи):
u |
|
t |
|
tи |
u |
|
h t d |
t |
u |
|
h |
t d |
||
22 |
|
11 |
|
12 |
||||||||||
|
|
|
|
u |
|
|
|
u |
||||||
|
|
|
3 |
0 |
|
|
|
|
tи |
|
|
|
||
|
2010 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
6 400e 400 t d 17879,7e 400t |
В. |
||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
В результате получим (рис. 7.11) |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
6 1 e 400t , |
0 t 20 мс |
||||||
|
|
|
|
u2 t |
400t, |
t 20 мс. |
||||||||
|
|
|
|
|
|
|
17879,7e |
|||||||
Рис. 7.11
113

ТЕМА 8. Частотный (спектральный) метод анализа переходных процессов в линейных электрических цепях
Лекция 14 Ряды Фурье. Теорема Парсеваля. Преобразование Фурье.
Спектральный метод анализа цепей
Различают:
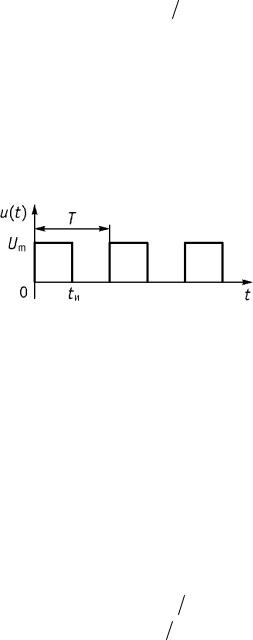
1.Частотный метод анализа при периодическом негармоническом воздействии, например, воздействие в виде последовательности прямоугольных импульсов или треугольных импульсов (рис. 8.1).
В этом случае входная последовательность (сигнал) представляется в виде ряда Фурье.
2.Частотный метод анализа при непериодическом негармоническом воздействии, например, воздействии в виде одиночного прямоугольного (рис. 8.2 а) или треугольного (рис. 8.2 б) импульсов. В этом случае входной сигнал представляется в виде интеграла Фурье.
Рис. 8.1 |
Рис. 8.2 |
Ряды Фурье. Краткие сведения
Если функция f t удовлетворяет условиям Дирихле:
1)имеет на периоде конечное число разрывов первого рода;
2)имеет конечное число максимумов и минимумов,
то она может быть разложена в ряд Фурье.
Различают тригонометрическую и комплексную формы ряда Фурье
|
1. Тригонометрическая форма f t u t |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
||
|
|
|
|
|
|
|
а) u t |
|
0 |
Ak cos k 1t k ; |
(8.1) |
|||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
2 |
k 1 |
|
||||
|
|
|
|
|
|
|
|
a0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
б) u t |
ak cos k 1t bk sin k 1t , |
(8.2) |
|||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
2 |
|
|
k 1 |
|
|
|
|||
|
A |
a |
0 |
|
1 T |
|
|
|
|
|
|
|
||||
где |
0 |
|
|
|
|
u t dt – среднее значение функции за период (постоянная со- |
||||||||||
|
2 |
T |
||||||||||||||
2 |
|
|
0 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
2T |
|
|
2T |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ставляющая); |
ak Akcos k |
|
u t cos k 1t dt; bk Aksin k |
|
u t sin k 1t dt; |
|||||||||||
T |
T |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
1 2 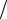 T .
T .
114
|
|
2. Комплексная форма ряда Фурье |
|
|
|
|
|
u t пункта б) |
|
||||||||||||||||||||
|
|
Комплексную форму получим, |
если в уравнение |
вместо |
|||||||||||||||||||||||||
cos k 1t и sin k 1t подставим их выражения в показательной форме |
|
|
|||||||||||||||||||||||||||
|
|
|
|
a |
0 |
|
e jk 1t e jk 1t |
|
e jk 1t e jk 1t |
|
a |
0 |
|
|
|
|
|||||||||||||
|
|
u t |
|
|
ak |
|
|
|
|
|
|
bk |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 j |
|
2 |
|
|
|
||||||||||
|
|
2 |
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(8.3) |
||||||||
1 |
|
|
jk t |
ak jbk e |
jk t |
a0 |
|
1 |
jk t |
|
|
|
|
jk t |
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
1 |
A k e |
|
1 |
|
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
ak jbk e |
|
|
|
|
|
|
2 |
|
|
Ake |
|
|
|
|
, |
||||||||||||||
|
2k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2k 1 |
|
|
|
|
|
|
|
|
|
|||||
где Ak ak jbk ; |
|
A k ak jbk . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Внесем под знак суммы слагаемое a0 2, тогда получим комплексную |
|||||||||||||||||||||||||||
форму ряда Фурье в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u t |
|
|
Ake jk 1t; |
Ak |
|
u t e jk 1tdt A k 1 e j k 1 , |
|
(8.4) |
|||||||||||||||||||
|
|
|
|
|
T |
|
|||||||||||||||||||||||
|
|
|
|
2k |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где A k 1 , k 1 – соответственно спектры амплитуд и фаз.
Ряд Фурье последовательности прямоугольных импульсов
Пусть имеется последовательность прямоугольных импульсов (рис. 8.3).
Рис. 8.3
Цель анализа: представить данную последовательность в виде ряда Фурье.
Порядок анализа
1. Определяем комплексные k-ые амплитуды напряжений
|
|
|
2T |
|
|
|
|
|
jk t |
|
|
|
|
|
|
2tи |
|
|
jk t |
|
|
|
|
2 |
T |
|
|
|
jk t |
||||||||||||||||||||||
U |
|
|
|
|
|
u t e |
|
|
1 dt |
|
|
|
|
|
u t e |
|
|
1 dt |
|
|
|
|
u t |
e |
|
1 dt |
|||||||||||||||||||||||||
|
T |
|
T |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
mk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tи |
0 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
2Umtи |
|
|
sin |
k 1tи |
|
|
|
|
jk t |
|
|
|
k t |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1 и |
jarg sin |
|
1 и |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
k t |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
. |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2. Находим амплитудный спектр |
|
|
|
|
|
|
|
sin k 1tи 2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
U k |
|
|
2Umtи |
|
|
|
|
|
, k 1,2,.... |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
k 1tи 2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
2U |
|
t |
и |
|
|
U 0 |
|
U |
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Для k = 0 U |
0 |
|
|
|
m |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
и |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
3. Находим фазовый спектр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
k |
|
k 1tи |
arg |
sin |
k 1tи |
|
, |
k 1,2,.... |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
(8.5)
(8.6)
(8.7)
115
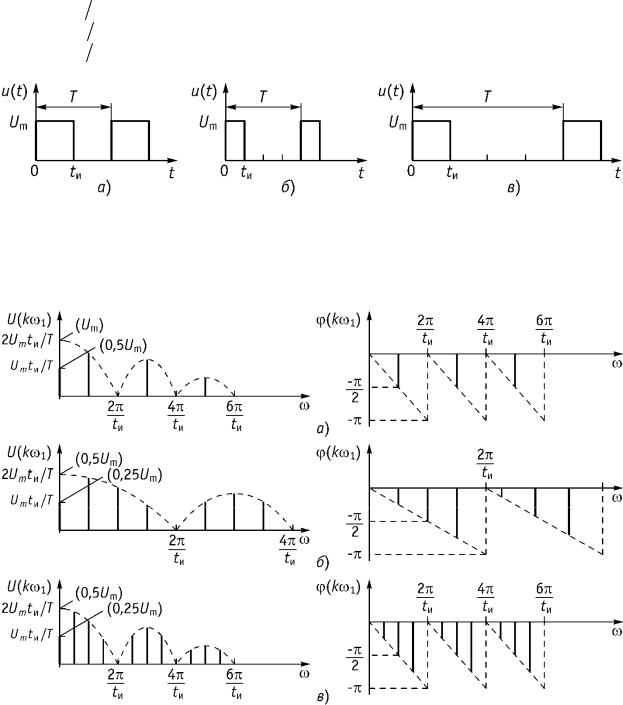
Видно, что амплитудный и фазовый спектры – дискретные спектры. Таким образом, последовательность прямоугольных импульсов имеет амплитудный и фазовый дискретные спектры.
4.Построим амплитудный и фазовый спектры для различных значений скважности q (q T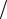 tи ):
tи ):
а) q T |
tи 2, период T const, |
tи |
=const , (рис. 8.4 |
а); |
б) q T |
tи 4, период T const, |
tи |
=var, (рис. 8.4 б); |
|
в) q T |
tи 4, период T var, tи |
=const , (рис. 8.4 в). |
|
|
Рис. 8.4
Амплитудный и фазовый спектры для случая а) приведены на рис. 8.5 а, для случая б) – на рис. 8.5 б, для случая в) – на рис. 8.5 в.
Рис. 8.5
Выводы
1.Огибающая амплитудного спектра изменяется по закону функции sinx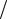 x.
x.
2.Огибающая имеет нули (амплитудный спектр равен нулю) на частотах
2 k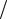 tи ( k = 1, 2, 3, …).
tи ( k = 1, 2, 3, …).
116

3.Спектр дискретный. Расстояние по частоте между гармоническими составляющими равно 1 2 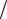 T .
T .
4.Количество составляющих между нулями равно q 1 (n q 1), где q – скважность, равная q = T/tи.
5.При T const и увеличении (уменьшении) tи расстояние между гармоническими составляющими остается постоянным, а расстояние между нулями огибающей уменьшается (увеличивается).
6.При tи const и увеличении (уменьшении) периода T расстояние между нулями огибающей остается постоянным, а расстояние между составляющими уменьшается (увеличивается).
Действующее и среднее значения напряжения и тока периодического негармонического сигнала. Равенство (теорема) Парсеваля
1. Действующие значения тока и напряжения
|
|
|
1T |
|
1T |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
I |
|
|
i2 t dt |
|
I0 |
Ikm cos k 1t k |
|
|
dt |
|
Ik2 ; U |
Uk2 . (8.8) |
||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
|
|
T |
0 |
|
T 0 |
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
k 0 |
k 0 |
|||||||||||||
2. |
Средние значения тока и напряжения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
1 T |
|
|
|
|
|
1 T |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
Iср |
|
0i t dt I0 ; |
Uср |
|
|
0u t dt U0. |
(8.9) |
|||||||||||||||||||||
|
|
|
|
|
|
T |
T |
|
||||||||||||||||||||||||||
3. |
Средние значения тока и напряжения по абсолютной величине |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Iср абс |
1 T |
|
i t |
|
dt; |
Uср абс |
1 T |
|
|
u t |
|
dt. |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
(8.10) |
|||||||||||||||||||
|
|
|
|
|
|
T |
|
|
T |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
4. |
Равенство (теорема) Парсеваля |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
P |
|
u2 t dt U02 Uk2 . |
|
|
|
|
(8.11) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
T 0 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|||||||
Активная, реактивная и полная мощности периодического негармонического сигнала (при периодическом негармоническом воздействии на цепь)
1. Активная мощность
|
1T |
1T |
|
|
|
|
|
|||||
P |
|
|
u t i t dt |
|
Umkcos k 1t |
k |
Imk cos k 1t k k dt |
|
||||
T |
T |
|
||||||||||
|
0 |
0 |
k 0 |
|
k 0 |
|
(8.12) |
|||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
UkIk cos k, |
|
|
|
|
|
|
|
|
||||
|
k 0 |
|
|
|
|
|
|
|
|
|
||
где k – угол между током и напряжением k-ой гармоники. |
|
|
||||||||||
2. Реактивная мощность |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q UkIk sin k . |
|
(8.13) |
||||
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
3. Полная мощность |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S UI |
|
Uk2 Ik2 . |
|
(8.14) |
||
|
|
|
|
|
|
|
|
k 0 |
k 0 |
|
|
|
117
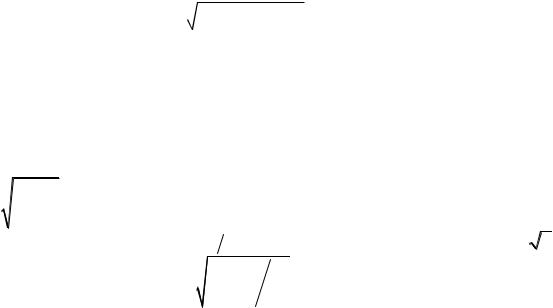
Замечание. Для негармонического сигнала S2 P2 Q2 .
4. Мощность искажения Pиск 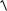
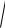 S2 P2 Q2 .
S2 P2 Q2 .
Коэффициенты, характеризующие периодическую негармоническую функцию(сигнал)
1.Коэффициент мощности kм P S .
S .
2.Коэффициент формы сигнала kф U1 Uср абс
Uср абс
ния kф 1,11).
3.Коэффициент искажения kи U1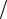 U , где U1
U , где U1
(для гармонического колеба-
– амплитуда первой гармони-
|
|
|
|
|
|
|
|
ки; U |
Uk2 . Для гармонического колебания kи 1. |
||||
|
|
k 0 |
|
|
|
|
4. |
Коэффициентамплитуды ka Um U (для гармонического колебания ka |
|
). |
|||
2 |
||||||
|
|
|
|
|
||
5. |
Коэффициент гармоник kг |
Uk2 U12 (для гармонического колебания |
||||
|
|
|
k 2 |
|||
kг 0).
Частотный метод анализа процессов в линейных электрических цепях при непериодическом негармоническом воздействии. Прямое и обратное преобразования Фурье. Свойства и теоремы преобразования Фурье
Если функция f t удовлетворяет: а) условию абсолютной интегрируемости
|
|
f t |
|
dt ; б) условию вида |
|
f t |
|
Me C0t , где M,C0 – положительные |
|
|
|
|
|||||
|
|
|
|
|
||||
|
|
|
|
|||||
|
|
|
|
|
|
|||
|
|
|
|
|
f t может быть преобразована по Фурье. |
|||
вещественные числа, то функция |
||||||||
Преобразования Фурье
Прямое преобразование Фурье (ППФ) позволяет определить комплекс-
ный спектр сигнала (комплексную спектральную плотность или спектр) по формуле
|
|
|
||
F j f t e j tdt A jB , |
(8.15) |
|||
|
|
|
||
где f t – функция; F j – изображение по Фурье. |
|
|||
Обратное преобразование Фурье (ОПФ) позволяет определить функцию |
||||
времени (оригинал) по Фурье-образу |
|
|||
|
1 |
|
|
|
f t |
F j e j td . |
(8.16) |
||
2 |
||||
|
|
|
||
Основные свойства преобразования Фурье |
|
|||
1. Если функция f t четная, то спектр F( j ) – вещественная величина |
|
|||
|
|
|
|
|
F( j ) f t cos tdt . |
(8.17) |
|||
118

2. Если функция |
f t |
нечетная, то спектр F( j ) – мнимая величина |
|
|
|
|
|
f t sin tdt. |
|
|
|
F( j ) j |
(8.18) |
|
|
f t |
|
|
|
3. Если функция |
четная, то в спектре (в сомножителе e j t ) можно поме- |
|||
нять «–» на «+» |
|
|
|
|
|
|
f t e j tdt . |
|
|
|
|
F( j ) |
(8.19) |
|
4.Свойство взаимозаменяемости переменной и t. Для четного сигнала и вещественного спектра
|
f t |
1 |
|
|
F( j )e j td ; |
|
|
|
|
|
|
|
(8.20) |
||||
|
2 |
|
||||||
|
|
|
|
|
|
|
||
|
f t e j tdt |
F( j ) |
f t , |
dt d . |
|
|||
F( j ) |
(8.21) |
|||||||
5.Сигнал f t может быть задан с помощью своего амплитудного и фазового
спектров ( F( j ) и F ), либо с помощью вещественной и мнимой частей спектра ( A и B ). Причем существует однозначная связь между модулем и фазой, между мнимой и действительной частями спектра. Эту связь можно показать на одностороннем сигнале
|
|
2 |
|
2 |
|
|
|
f t |
A cos td |
B sin td . |
(8.22) |
||
|
|
|
||||
|
|
0 |
0 |
|
||
6. |
Преобразование Фурье является однозначным: сигналу f t |
соответствует |
||||
|
только одно преобразование Фурье F( j ) |
и преобразованию Фурье F( j ) |
||||
|
соответствует только один сигнал. |
|
|
|
||
|
Основные теоремы преобразования Фурье |
|
||||
1. |
Теорема линейности |
|
|
|
|
|
|
|
|
|
|
ak fk |
t akFk ( j ). |
|
(8.23) |
||||||||||||
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
2. |
Сдвиг функции (сигнала) во времени |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
f t t0 e j t0 F |
j . |
|
(8.24) |
||||||||||||
3. |
Изменение масштаба переменной t |
|
|
|
j |
|
|
|||||||||||||
|
|
|
|
|
|
f at |
|
1 |
F |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
(8.25) |
||||||
|
|
|
|
|
|
|
a |
a |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f1 t и |
f2 t со- |
||||
4. |
Теорема свертки: произведению двух функций (сигналов) |
|||||||||||||||||||
|
ответствует свертка их спектров |
F |
|
|
|
|
|
|
|
|
||||||||||
|
f |
1 |
t f |
2 |
t |
|
1 |
|
j |
F |
j j d . |
|
(8.26) |
|||||||
|
|
|
||||||||||||||||||
|
|
|
|
|
2 |
|
|
1 |
|
|
|
2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
119
5. |
Произведение спектров двух сигналов соответствует свертке сигналов |
|||||||||||
|
F ( j )F |
( j ) |
|
|
f |
|
f |
|
t d . |
|
||
|
|
|
1 |
2 |
(8.27) |
|||||||
|
1 |
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
6. |
Смещение спектра на частоту 1 |
|
|
|
|
|
|
|||||
|
|
F( j j 1) e j 1t |
f t . |
(8.28) |
||||||||
7. |
Дифференцирование спектра |
|
|
|
|
|
|
|
|
|||
|
|
|
dF j |
( jt) f t . |
(8.29) |
|||||||
|
|
|
|
|||||||||
|
|
|
|
d |
|
|
|
|
|
|
|
|
8. Дифференцирование и интегрирование сигнала
d f t |
|
t |
|
1 |
|
|
|
|
j F j f 0 |
; |
|
f t dt |
|
F j . |
(8.30) |
|
|
||||||
dt |
|
|
|
j |
|
||
120
