
515_Teorija Ehlektricheskikh Tsepej
.pdfПорядок анализа
1. Определяем количество отсчетов N выходного сигнала (результата линейной свертки) по формуле
N N1 N2 1. |
(9.51) |
2.Дополняем справа последовательность входного сигнала нулями, количество нулей равно N2 – 1.
3.Дополняем справа последовательность импульсной характеристики нулями, количество нулей равно N1 – 1.
4.Определяем выходную последовательность (выходной сигнал) по формуле линейной дискретной свертки
N 1 |
|
y mT x nT h mT nT . |
(9.52) |
n 0
Метод круговой свертки
Метод основан на свойстве круговой свертки: свертка сигналов x1(n) и x2(n) соответствует произведению ДПФ сигналов.
x n x |
2 |
n X |
1 |
k X |
2 |
k . |
(9.53) |
1 |
|
|
|
|
Заметим, что формула круговой свертки (9.53) применима к периодическому входному дискретному сигналу и импульсной характеристике, имеющих равные периоды N, причем круговая свертка также выполняется на периоде в N отсчетов. Для того чтобы результат круговой свертки соответствовал результату линейной свертки, период круговой свертки должен соответствовать длине линейной свертки. Алгоритм круговой свертки:
1. Вычисляем ДПФ входной последовательности x(n)
|
N 1 |
j |
|
2 |
|
nk |
|
||||
|
|
|
|
(9.54) |
|||||||
|
X k x nT e |
|
|
N . |
|||||||
|
n 0 |
|
|
|
|
|
|
|
|
||
2. |
Вычисляем ДПФ импульсной характеристики h(n) |
|
|||||||||
|
N 1 |
j |
2 |
nk |
|
||||||
|
|
|
(9.55) |
||||||||
|
H k h nT e |
|
|
N . |
|||||||
|
n 0 |
|
|
|
|
|
|
|
|
||
3. |
Вычисляем ДПФ выходной последовательности y(n) |
|
|||||||||
|
Y k X k H k . |
(9.56) |
|||||||||
4. |
Определяем выходную последовательность по формуле обратного ДПФ |
||||||||||
|
|
1 |
N 1 |
j |
2 |
nk |
|
||||
|
|
|
|
||||||||
|
y nT |
Y k e N . |
(9.57) |
||||||||
|
|
||||||||||
|
|
N k 0 |
|
|
|
|
|
|
|
|
|
141
Примеры и задачи
Пример 1. Дана последовательность х nT e nT , n = 0, 1, 2 ,…; α < 0. Найти спектр этой последовательности.
Решение
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||||
|
|
|
X e j T x nT e j nT e nT e j nT |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
1 e( j )T |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
n 0 |
|
|
|
|
|
|
|
|
|
|
n 0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
e arctg |
e |
T |
|
|
|
|
1 e |
T |
cos T |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
sin T/ |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
1 e T cos T 2 e T cos T 2 |
|
|
|
|
||||||||||||||||||||||||||||
|
Пример 2. Последовательность x nT e nT , n = 0, 1, 2, …; α < 0 умножа- |
||||||||||||||||||||||||||||||||||||||
ется на e j 1 nT . Найти спектр сигнала x |
|
nT e nT e j 1nT . |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Используем свойство |
смещения |
|
в |
области |
|
комплексного |
переменного |
|||||||||||||||||||||||||||||||
(сдвиг спектра Xд j |
последовательности x nT |
|
по оси частот) |
||||||||||||||||||||||||||||||||||||
X1 e j T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
e nT e j( 1)nT e nT |
cos( 1)nT j e nT |
sin( 1)nT |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
n 0 |
|
|
|
|
|
|
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 0 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e nT sin( )nT |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jarctg |
n 0 |
1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e nT cos( )nT |
|||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
nT |
|
|
|
|
|
|
|
|
|
nT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 0 |
1 |
|
|||||||
|
e |
cos( 1)nT |
|
e |
sin( 1)nT |
|
e |
|
|
|
|
. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
n 0 |
|
|
|
|
|
|
|
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Поскольку X1 e |
j T |
|
|
|
( j( 1))nT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
e |
является |
сходящейся |
геометриче- |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ской прогрессией, спектр равен X1 e j T |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
. Если ω1 = π/Т, тогда |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 e |
( j( 1))T |
|
|
|
|
|||||||||||||||
X1 nT ( 1)ne nT , и спектр равен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
X1 e j T |
|
|
|
|
|
1 |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
( j( |
|
|
))T |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 e |
T 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Пример 3. Определить z-изображение дискретного импульса |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
1 |
|
при |
п 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
при |
п 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Решение Воспользуемся формулой z-изображения
Z( n ) n z n 0 z 0 1.
n 0
142

Пример 4. Определить z-изображение задержанного на m отсчетов дискретного импульса
|
1при |
п m |
n m |
0 при |
п m. |
|
Решение Используя теорему запаздывания, имеем
Z( n m ) n m z n Z( n )z m z m.
n
Пример 5. Определить z-изображение дискретной ступенчатой функция u n
|
1 при |
п 0 |
u n |
||
|
0 при |
п 0. |
Решение Воспользуемся формулой z-изображения
|
|
|
z 1 n . |
Z(u n ) u n z n z n |
|||
n 0 |
n 0 |
n 0 |
|
n
Если |z| > |
1, тогда z 1 |
(выполняется условие сходимости) и ряд |
||
|
n 0 |
|
|
|
|
|
|
|
|
z 1 n |
сходится и представляет сумму членов бесконечной геометрической |
|||
n 0 |
|
|
|
|
прогрессии, равную |
|
|
|
|
|
|
|
1 |
|
|
Z(u n ) z 1 n |
. |
||
|
|
|||
|
|
n 0 |
1 z 1 |
|
Пример 6. Определить z-изображение задержанной на m отсчетов дискретной ступенчатой функция u n m
|
1 при |
п m |
u n m |
0 при |
п m. |
|
Решение Используя теорему запаздывания, имеем
|
z |
m |
|
|
Z(u n m ) u n m z n Z(u n )z m |
|
. |
||
1 z 1 |
||||
n |
|
|||
Пример 7. Задана последовательность
x n 1 при n 0 0 при n 0.
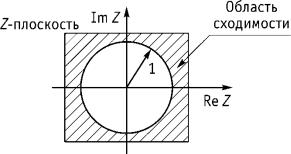
Определить область сходимости z-преобразования последовательности х(n) и границу области сходимости.
143
Решение
Определяем Z-преобразование последовательности х(n)
|
|
|
|
|
|
|
|
|
|
|
|
n . |
|
|
Х z Z(x n ) x n z n z n z 1 |
||||||||||
|
|
|
n 0 |
|
n 0 |
n 0 |
|
|||||
Следовательно, X re j T |
|
n |
|
r 1 |
n e j Tn . |
|
||||||
re j T |
|
|
||||||||||
|
|
|
n 0 |
|
n 0 |
|
|
|
|
|
|
|
|
Областью сходимости являются значения z с радиусом r, для которых |
|||||||||||
|
|
n |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
r 1 |
. Это условие выполняется, |
если |
|
|
|
1. Следовательно, областью |
|||||
|
r |
|||||||||||
n 0 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
сходимости х(z) является часть Z-плоскости вне круга радиуса 1, как показано на рис. 9.14.
Граница сходимости z-преобразования последовательности х(n) – это значения Z с радиусом 1. Радиус сходимости R последовательности х(n) равен: R = 1.
Рис. 9.14
Пример 8. Имеется периодическая последовательность хp(n) вида
xp n an |
для 0 n N 1 |
и xp n mN xp n , |
|
a |
|
1, |
|
|
|||||
|
|
где m – целое число.
Найти ДПФ периодической последовательности хp(n) и показать периодичность ДПФ.
Решение
|
|
2 k |
|
1 aNe j |
2 k |
N |
|
1 aN |
|||||||
N 1 |
j |
n |
N |
|
|||||||||||
|
|
||||||||||||||
X p k ane N |
|
|
|
|
|
|
|
|
. |
||||||
|
2 k |
|
|
|
|||||||||||
n 0 |
|
|
|
|
j |
|
|
|
j |
2 k |
|||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
1 ae |
N |
|
1 ae |
N |
||||||
Покажем периодичность ДПФ:
X |
p |
k mN |
1 aN |
|
|
1 aN |
|
X |
p |
k . |
||
|
j2 (k mN) |
|
|
j2 k |
|
|||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 ae |
N |
|
|
1 ae |
N |
|
|
|
|
Пример 9. Имеются две последовательности с периодом N = 3 х1(n) = {0.0; 1.0; 2.0} и х2(n) = {1.0; –1.0; 0.0} (рис. 9.15). Найти круговую свертку сигналов.
144
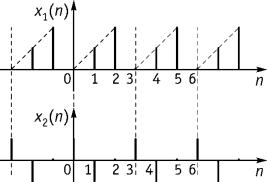
Рис. 9.15 |
|
Решение 1 |
|
Воспользуемся формулой круговой свертки |
|
N 1 |
2 |
y n x1 m x2 n m mod N |
x1 m x2 n m mod N . |
m 0 |
m 0 |
y(0) = х1(0) х2(0)+ х1(1) х2(-1)+ х1(2) х2(-2)=0 1+1 0+2 (-1) = -2 (х2(0-k)={1; 0;-1}).
y(1) = х1(0) х2(1)+ х1(1) х2(0)+ х1(2) х2(-1)=0 (-1)+1 1+2 0=1 |
(х2(1-k)={-1;1;0}). |
||||||||||||||||||
y(2) = х1(0) х2(2)+ х1(1) х2(1)+ х1(2) х2(0)=0 0+1 (-1)+2 1=1 |
(х2(2-k)={0;-1;1}). |
||||||||||||||||||
|
|
Y(n) = {-2, 1, 1}. Или |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х1(k) |
0 |
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||
|
х2(0-k) |
1 |
|
0 |
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
||
|
y(0) = |
0 + |
|
0 |
|
|
|
-2 = -2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х1(k) |
0 |
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
х2(1-k) |
-1 |
|
1 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
y(1) = |
0 + |
|
1 |
|
+ |
|
|
0 = 1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
х1(k) |
0 |
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
х2(2-k) |
0 |
|
-1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
|
y(2) = |
0 |
|
-1 |
+ |
|
2 = 1 |
|
|
|
|
|
|
|
|||||
|
|
|
Решение 2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
Воспользуемся формулой круговой свертки в виде |
|
|
|
|
|
||||||||||||||
|
N 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yp n x1 m x2 n m mod N X1 k X 2 k |
Y |
p k . |
|||||||||||||||||
|
m 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.Определяем ДПФ сигналов х1(n) = {0.0; 1.0; 2.0} и х2(n) = {1.0; –1.0; 0.0} |
|||||||||||||||||||
2 |
|
j |
2 |
kn |
|
|
|
j |
2 |
k1 |
|
j |
2 |
k2 |
|||||
|
|
|
|
|
|
|
|
||||||||||||
X1 k x1 n e 3 |
0 e 3 |
2e 3 . |
|||||||||||||||||
n 0
Х1(0) = 0+1+2=3, X1(1)=0+cos120˚– jsin120˚+2cos240˚– j2sin240˚= –1,5+ j0,866, X1(2) = 0+cos240˚– jsin240˚+2cos480˚– j2sin480˚= –1,5– j0,866.
145
2 |
j |
2 |
kn |
|
j |
2 |
k1 |
|
|
|
|||||
X 2 k x2 n e |
3 |
|
1 e |
|
3 0. |
||
n 0 |
|
|
|
|
|
|
|
Х2(0) = 1 – 1+ 0 = 0, X2(1) = 1 – cos120˚+ jsin120˚= 1,5 + j0.866, X2(2) = 1 – cos240˚ + jsin240˚ = 1,5 – j0,866.
2. Определяем ДПФ выходного сигнала
Y(k)=X1(k)*X2(k)={0; -1,5+j0,866; -1,5-j0,866}{0;1,5+j0,866; 1,5-j0,866}= ={0;-3;-3;}.
3. Определяем выходную последовательность y(n), используя формулу обратного ДПФ
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
j |
|
2 |
|
n0 |
j |
2 |
n1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1 |
N 1 |
j |
kn |
1 |
2 |
j |
kn |
1 |
Y 0 e |
3 |
|
|
Y 1 e 3 |
||||||||||||
|
|
||||||||||||||||||||||||
y n |
|
Y k e |
|
N |
|
|
Y k e |
3 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||
N |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
k 0 |
|
|
|
3 |
k 0 |
|
|
|
3 |
|
j |
n2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
e |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y 2 |
3 |
|
|
|
|
|
||||
=
= 1/3{0 – 3[cos(n120˚) + jsin(n120˚) – 3[cos(n240˚) + jsin(n240˚)]}. y(0) = (1/3)(-3-3) = –2; у(1) = (1/3)(3/2– 3j0,866+3/2 + 3j0,866) = 1;
у(2) = (1/3)(3/2 + 3j0,866 + 3/2 – 3j0,866) = 1. Y(n) = {-2;1;1}. Видно, что полученный результат совпадает с решением 1.
Пример 10. Разностное уравнение цепи имеет вид
y nT 0,6y nT T 0,05y nT 2T x nT .
Необходимо: 1) привести схему дискретной цепи; 2) найти выходной сигнал и два первых отсчета сигнала для нулевых начальных условий у(–1T) = 0 и у(–2T)
=0, если входной сигнал равен
xnT e jn, n = 0, 1, 2, ….
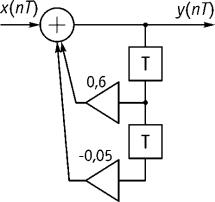
Решение 1. По виду разностного уравнения, учитывая прямые и обратные связи,
приведем схему дискретной цепи (рис. 9.16).
Рис. 9.16
146
2. Применим Z-преобразование к правой и левой частям разностного уравнения
Y z 0,6Y z z 1 0,05Y z z 2 X z . 3. Найдем передаточную функцию цепи
H z |
Y z |
1 |
. |
||
|
|
|
|
||
|
1 0,6z 1 |
0,05z 2 |
|||
|
X z |
|
|||
4. Найдем Z-преобразование входного сигнала
|
|
1 |
|
|
X z x nT z n e jn z n |
. |
|||
1 e j z 1 |
||||
n 0 |
n 0 |
|
||
5. Находим Z-преобразование выходного сигнала Y(z)
Y z H z X z |
1 |
|
1 |
|
. |
1 0,6z 1 0,05z 2 |
1 e j |
|
|||
|
z 1 |
||||
6.Определяем полюсы функции Y(z)
1 0,6z 1 0,05z 2 1 e jz 1 0.
|
|
|
|
|
|
z1 = 0,5, z2 = 0,1, z3 = e j . |
|
|
|
|
|
|
|
||||||||||||||
7. Находим вычеты и определяем сигнал y(n) |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
ResF(z) Res X z zn 1 |
|
0,5n 2 |
|
, |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
z1 |
z1 |
|
|
|
|
|
|
|
|
|
0,2 0,4e j |
|
|||||||||
|
|
|
ResF(z) Res X z zn 1 |
|
|
0,1n 2 |
|
, |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
z2 |
z2 |
|
|
|
|
|
|
|
0,04 0,4e j |
|
|||||||||||||
|
ResF(z) Res |
X z zn 1 |
|
|
|
|
|
ej(n 2) |
|
|
|
|
|
|
. |
||||||||||||
e j |
0,5 e j |
0,1 |
|||||||||||||||||||||||||
|
z3 |
|
|
z3 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
y n ResF(z) ResF(z) ResF(z) |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
z1 |
|
|
z2 |
|
|
|
|
|
|
|
z3 |
|
|
|
|
|
|
|
||
|
|
|
|
0,5n 2 |
|
0,1n 2 |
|
|
|
|
|
|
|
e j n 2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
||||||||
|
|
|
|
0,04 0,4e j |
|
(e j 0,5)(e j |
|
|
|
||||||||||||||||||
|
|
|
0,2 0,4e j |
|
|
|
|
0,1) |
|
||||||||||||||||||
8. Определяем первые два отсчета сигнала по формуле и по разностному |
|||||||||||||||||||||||||||
уравнению. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
По формуле: |
|
y n ResF(z) ResF(z) ResF(z) |
|
||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
z1 |
|
|
z2 |
|
|
|
|
|
|
|
z3 |
|
|
|
|
|
|
|
||
|
|
|
|
0,5n 2 |
|
0,1n 2 |
|
|
|
|
|
|
|
e j n 2 |
|
|
|
, |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
0,04 0,4e j |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
0,2 0,4ej |
|
|
|
|
(e j 0,5)(e j |
0,1) |
|
|||||||||||||||||
y 0 0,0355 j0,7411 0,0122 j0,0233 1,0234 j0,7178 1 |
|||||||||||||||||||||||||||
y 1 |
0,53 |
|
0,13 |
|
|
|
e j3 |
|
|
1,1402 j0,8415 (Здесь |
|||||||||||||||||
0,2 0,4e j |
|
0,04 0,4e j |
(e j 0,5)(e j |
|
|
||||||||||||||||||||||
|
|
|
|
0,1) |
|
|
|
|
|
|
|
||||||||||||||||
углы при экспоненте выражаются в радианах).
147
По разностному уравнению:
y 0T 0,6y 0T T 0,05y 0T 2T х 0T e j0 1,
y 1T 0,6y T T 0,05y T 2T х 1T 0,6 e j10,6 0,5403 j0,8415 1,1403 j0,8415.
Задача 1. Имеется последовательность x(n) ограниченной длительности
x n 1 для 0 n N 1
0 для n 0, n N 1.
1. Найти ДПФ последовательности x(n) при N = 5. 2. Построить амплитудный и фазовый спектры ДПФ. 3. Сравнить амплитудный и фазовый спектр ДПФ с амплитудным и фазовым спектрами преобразования Фурье последовательности x(n).
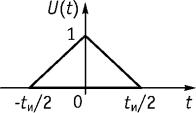
Задача 2. Задан аналоговый сигнал в виде треугольного импульса, амплитуда сигнала равна 1 В, длительность сигнала равна 4 мкс (рис. 9.17). Определить интервал и частоту дискретизации, полагая, что граничная (верхняя) частота сигнала находится из условия, что на частотах, выше граничной, все значения модуля спектральной плотности более, чем в 10 раз меньше максимального значения.
Рис. 9.17
Задача 3. Задана передаточная функция цепи |
H z |
1 |
|
. Необхо- |
1 0,5z |
|
|||
|
|
1 |
||
димо определить сумму квадратов отсчетов импульсной характеристики
h2 nT .
n 0
Задача 4. |
Задана конечная импульсная |
характеристика h nT |
0.0; 1.0; 2.0 |
дискретной цепи. Необходимо найти передаточную функцию |
|
H z и комплексную частотную характеристику |
H e j T дискретной цепи. |
|
Построить графики АЧХ и ФЧХ дискретной цепи.
148

