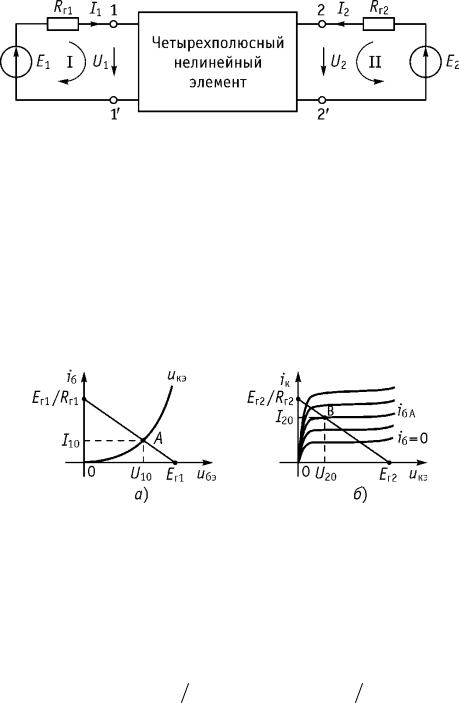
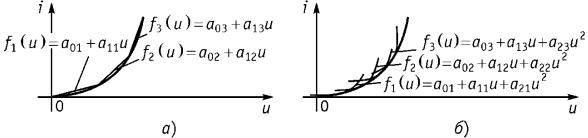
i = 1, …, N – количество неизвестных коэффициентов (количество узлов интерполяции). Аппроксимация называется интерполяцией
Недостаток: отсутствует процедура выбора узлов интерполяции;
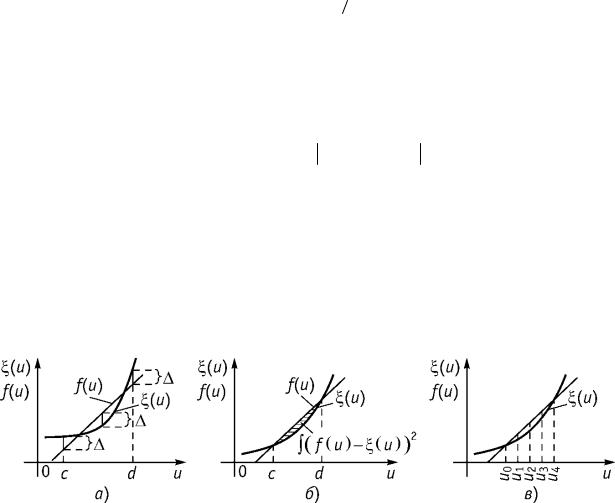
г) приближение по Тейлору – значение аппроксимирующей функции f(u) и аппроксимируемой функции (u) и их N – 1 значений производных совпадают в выбранной точке U0
f U0, a1, ,aN U0 ,
f U0, a1, ,aN U0 |
, |
|
(11.23) |
|
f N 1 U0, a1, ,aN N 1 U0 ,
где N – количество неизвестных коэффициентов.
3.Составляем систему уравнений, из которой определяем коэффициенты.
4.Записываем аппроксимирующую функцию f(u).
Всоответствии с общим порядком решения задачи аппроксимации находим аппроксимирующую функцию для различных критериев приближения.
Аппроксимация по среднеквадратическому критерию приближения
min |
1 |
M |
(11.24) |
f uk uk 2 . |
a0, ,aN M k 1
1.Выбираем аппроксимирующую функцию f(u) в виде степенного ряда (полином 2-ой степени, s = 2)
|
|
|
|
f u a |
0 |
a u a |
2 |
u2 . |
|
|
|
|
|
|
(11.25) |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
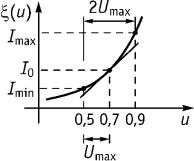
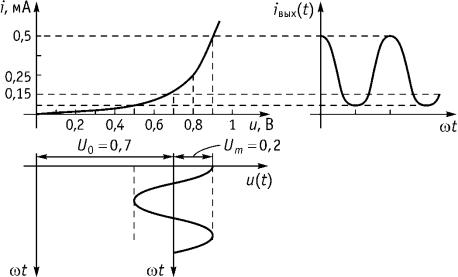
2. Аппроксимируем |
ВАХ степенным |
рядом |
|
относительно |
точки U0 |
(U0 0,7 табл. 13) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f u a |
0 |
a |
1 |
u 0,7 a |
2 |
u 0,7 2 a |
0 |
a u |
a |
2 |
u |
2 . |
(11.26) |
|
|
|
|
|
|
|
|
1 н |
|
|
н |
|
3. Определяем значения uн в точках 0,4, …, 0,9; M = 5 k = 1: uн1 0,4 0,7 0,3; uн21 0,09;
k = 2: uн2 |
0,5 0,7 |
0,2; |
uн22 0,04; |
|
k = 3: uн3 0,7 0,7 0; uн23 |
0; |
(11.27) |
k = 4: uн4 |
0,8 0,7 |
0,1; uн24 0,01; |
|
k= 5: uн5 0,9 0,7 0,2; uн25 0,04.
4.Получим систему уравнений для определения неизвестных коэффициен-
|
|
|
1 |
M |
|
тов a0, a1 |
и a2, взяв производные от функции |
f uk uk 2 по |
|
|
|
|
|
M k 1 |
этим коэффициентам и приравняв их нулю (минимумы функции )