2.4. Соотношение неопределенностей Шредингера- Робертсона

Неравенство, предложенное Шредингером и Робертсоном, отражает в себе свойства, присущие как неравенству Коши- Буняковского, так и соотношению неопределенностей Гейзенберга и, в известном смысле, может считаться их обобщением [35,36].

Пусть и - две произвольные наблюдаемые. Без ограничения общности будем считать их центрированными: .

Рассмотрим следующее заведомо неотрицательное выражение:

Здесь - произвольное действительное число, - тоже действительное, но фиксированное число (фаза, выбор которой мы осуществим позднее).

Определим ковариацию величин как

Заметим, что симметризация произведения наблюдаемых потребовалась нам, чтобы сделать соответствующий оператор эрмитовым.

Пусть:

,

где - эрмитов оператор. Тогда:

В развернутой записи выражение для имеет вид:

Пусть:

,

Очевидно, можно найти такой угол , чтобы выполнялись тождества:

Тогда:

Распорядимся произволом в выборе фазы , чтобы обеспечить выполнение равенства . Указанный выбор, очевидно, обеспечит получение наиболее сильного неравенства:

Определим коэффициент корреляции между наблюдаемыми и как:

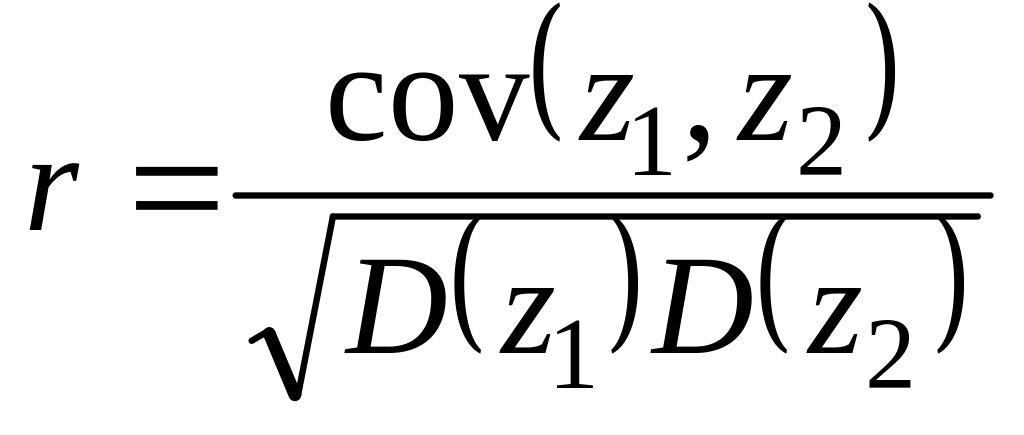
В результате, искомое неравенство (соотношение неопределенностей Шредингера- Робертсона) примет вид:

,

где

Введенный параметр есть аналог известного числа Шмидта [37]. Это число имеет фундаментальное значение для описания квантовых корреляций и квантовой информации (см. Приложение к Главе 3).

Пусть теперь рассматриваемые наблюдаемые есть операторы координаты и импульса соответственно:

, .

Тогда, в силу фундаментального перестановочного соотношения для координаты и импульса, есть тождественный оператор (единичная матрица).

В этом случае соотношение неопределенностей Шредингера- Робертсона будет иметь вид:

Пусть , - неопределенности (стандартные отклонения) для координаты и импульса. Тогда:

Таким образом, если координата и импульс коррелируют друг с другом, произведение их неопределенностей возрастает в раз по сравнению с величиной, определяемой неравенством Гейзенберга.

Заметим, что в силу некоммутативности координаты и импульса, их квантовая ковариация не может быть оценена по выборке подобно классической ковариации. Для вычисления соответствующей оценки нужно знать априори (или оценить по результатам взаимно- дополнительных измерений) вектор состояния (волновую функцию). Пусть:

,

где действительные функции и есть соответственно плотность и фаза пси- функции. Заметим, что фаза есть аналог классического действия механической системы.

Используя функции плотности и фазы, нетрудно получить следующее простое представление для ковариации координаты и импульса:

Наглядность полученного результата обусловлена тем, что в классической механике производная от функции действия есть импульс.

2.5. Многомерное соотношение неопределенностей

Рассмотрим пространство размерности .

Пусть - соответствующие операторы координат и импульсов.

Вывод соотношения неопределенности в многомерном случае аналогичен одномерному, но теперь вместо действительного числа следует ввести действительную симметричную матрицу с элементами . Такое видоизменение диктуется необходимостью придать рассматриваемым величинам геометрически инвариантный вид в гильбертовом пространстве. Действительно для скалярного , такая величина как неинвариантна, потому что индексы и , вообще говоря, различны. В то же время, для матрицы величина будет кет- вектором в гильбертовом пространстве (по повторяющемуся индексу предполагается суммирование). Введем также действительный вектор ( ). С его помощью, взяв скалярное произведение, преобразуем полученный кет- вектор в скаляр: .

Рассмотрим теперь следующее заведомо неотрицательное выражение (по повторяющимся индексам, как обычно, предполагается суммирование):

В развернутом виде получим:

Чтобы использовать фундаментальные коммутационные соотношения между координатой и импульсом, перепишем последнее выражение, осуществив замену индексов и друг на друга, после чего сложим полученное выражение с исходным.

В качестве наблюдаемых будем использовать центрированные координаты и импульсы (имеющие нулевые средние).

В результате получим условие, согласно которому нижеследующее матричное выражение является неотрицательно определенным:

Напомним, что матрица с элементами называется неотрицательно определенной, если для любого вектора :

В полученном неравенстве мы ввели матрицы ковариаций координат и импульсов. Элементы этих матриц определяются выражениями

Учтем, что неотрицательная определенность матрицы ковариаций импульсов позволяет определить квадратный корень из нее.

Напомним, что произвольная эрмитова матрица может быть приведена к диагональному виду, т.е. может быть представлена как:

,

где - унитарная матрица, а - действительная диагональная матрица.

Если, к тому же, матрица неотрицательно определена, то неотрицательны и ее собственные значения, образующие диагональ матрицы . В этом случае операция взятия квадратного корня из матрицы является хорошо определенной:

С использованием понятия матричного квадратного корня, полученное выше неравенство можно представить в виде:

Первое слагаемое слева заведомо неотрицательно определено (и обращается в ноль при ). Отсюда следует, что и выражение неотрицательно определено, т.е.

Полученное неравенство и есть искомое многомерное соотношение неопределенностей. Его смысл заключается в следующем: каково бы ни было квантовое состояние, матрица, равная разности между матрицей ковариации координат и одной четвертой от матрицы, обратной к матрице ковариации импульсов, всегда является неотрицательно определенной.

Из приведенных расчетов следует, что неравенство обращается в равенство в том и только том случае, когда вектор состояния удовлетворяет следующему условию при :

Отсюда получаем, что соответствующее состояние является гауссовским с матрицей ковариаций в импульсном представлении и матрицей ковариаций - в координатном.

Мы ограничились рассмотрением многомерного соотношения неопределенностей, которое является непосредственным обобщением одномерного соотношения неопределенностей Гейзенберга. Другие примеры обобщенных соотношений неопределенностей и, в частности, связанные с обобщением соотношения Шредингера- Робертсона можно найти в [35,36]