
- •Часть 1
- •Оглавление
- •Введение
- •1. Источники и причины погрешностей математической модели
- •Погрешность математической модели
- •Погрешность исходных данных
- •Погрешность численного метода
- •Погрешность проведения расчетов на вычислительных машинах
- •Погрешности округления чисел в эвм
- •Погрешность результатов вычисления арифметических операций
- •“Потеря порядка” и “переполнение” при проведении вычислений на эвм
- •Машинная реализация вычислений
- •Контрольные вопросы и задания
- •2. Системы линейных алгебраических уравнений
- •Прямые методы решения
- •Метод Гаусса
- •Определение числа операций алгоритма метода Гаусса
- •Вычисление определителя матрицы
- •Построение обратной матрицы
- •Метод квадратного корня
- •Определение числа операций алгоритма метода квадратного корня
- •Устойчивость системы линейных алгебраических уравнений
- •Итерационные методы решения
- •Метод Якоби1
- •Метод Зейделя1
- •Сходимость итерационных методов
- •Скорость сходимости
- •Полиномы Чебышёва1
- •Итерационный метод с чебышёвским набором параметров
- •Неявный метод с чебышёвским набором параметров
- •Метод минимальных невязок
- •Метод минимальных поправок
- •Метод скорейшего спуска
- •Неявный метод скорейшего спуска
- •Контрольные вопросы и задания
- •3.НелинейныЕ уравнения
- •Методы вычисления корней нелинейного уравнения1 Метод половинного деления2
- •Метод простых итераций
- •Метод Ньютона2
- •Модификации метода Ньютона
- •Системы нелинейных уравнений
- •Метод простых итераций
- •Метод релаксации
- •Метод Ньютона
- •Нелинейный вариант метода Якоби
- •Нелинейный вариант метода Зейделя
- •Контрольные вопросы и задания
- •Интерполяция степенными функциями
- •Интерполяционный многочлен Ньютона
- •Интерполяционная формула Лагранжа
- •Погрешность полинома Ньютона (Лагранжа)
- •Сходимость интерполяционного процесса
- •Интерполяционный многочлен Эрмита1
- •Интерполяция сплайнами
- •Построение кубического сплайна
- •Сходимость процесса интерполяции кубическими сплайнами
- •Наилучшее приближение в гильбертовом пространстве
- •Метод наименьших квадратов
- •Контрольные вопросы и задания
- •5. Алгебраическая проблема собственных значений
- •Устойчивость собственных значений и векторов
- •Определение собственных значений и векторов Метод интерполяции
- •Трехдиагональные матрицы
- •Поиск собственных векторов
- •Частичная проблема собственных значений
- •Метод линеаризации
- •Степенной метод
- •Метод обратных итераций
- •Контрольные вопросы и задания
- •6.Численное дифференцирование Конечно-разностная аппроксимация
- •Применение интерполяционных формул
- •Контрольные вопросы и задания
- •7.Численное интегрирование
- •Формула прямоугольников
- •Формула трапеций
- •Формула Симпсона1
- •Формула Эйлера1
- •Оценка погрешности методом Рунге2
5. Алгебраическая проблема собственных значений
Пусть А - квадратная матрица размером
![]() ;
если существуют такие векторы
;
если существуют такие векторы
![]() ,
что
,
что
![]() , (5.1)
, (5.1)
то называется собственным значением, а X - собственным вектором матрицы A, соответствующим этому собственному значению.
В иной записи,
![]() .
(5.2)
.
(5.2)
Очевидно, что система линейных однородных алгебраических уравнений (5.2) имеет нетривиальное решение лишь в случае
 .
.
Понятно, что характеристический
многочлен
![]() является полиномом степени n от переменной
. Это, в свою очередь,
означает, что существует n корней
характеристического многочлена, и,
следовательно, имеется n собственных
значений
и соответствующих им собственных
векторов
является полиномом степени n от переменной
. Это, в свою очередь,
означает, что существует n корней
характеристического многочлена, и,
следовательно, имеется n собственных
значений
и соответствующих им собственных
векторов
![]() для матрицы A.
для матрицы A.
Пример 5.1. Пусть задана матрица
![]() .
.
Требуется определить собственные значения и векторы этой матрицы.
Характеристический многочлен:
 .
.
Собственные значения:
![]() .
.
Определим первый собственный вектор,
соответствующий
![]() ,
,
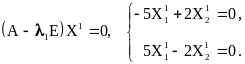
Здесь обозначено:
![]() - компоненты вектора
- компоненты вектора
![]() .
.
Очевидно, что последняя система содержит
линейно зависимые уравнения (как это и
следовало ожидать при
![]() ).
Используя любое из уравнений этой
системы, получим
).
Используя любое из уравнений этой
системы, получим
![]() .
.
Примем для однозначности определения
собственных векторов условие нормирования
![]() ,
то есть
,
то есть
![]() ,
,
![]() ,
,
![]() .
.
Теперь найдем второй собственный вектор,
соответствующий
![]() ,
,

Отсюда получаем связь компонент второго
собственного вектора:
![]() .
.
Из условия нормирования следует:
![]() ,
,
![]() ,
,
![]() .
.
Устойчивость собственных значений и векторов
Рассмотрим две матрицы, A и
![]() .
Собственные числа обеих матриц, в чем
нетрудно убедиться, одинаковы. Собственные
векторы матриц обозначим соответственно
.
Собственные числа обеих матриц, в чем
нетрудно убедиться, одинаковы. Собственные
векторы матриц обозначим соответственно
![]() :
:
![]() .
.
Для скалярных произведений
![]() и
и
![]() вычислим разность
вычислим разность
![]() .
.
Поскольку
![]() , (5.3)
, (5.3)
получаем:
![]() .
.
Отсюда следует, что для различных
собственных значений,
![]() ,
собственные векторы матриц A и
взаимно ортогональны.
,
собственные векторы матриц A и
взаимно ортогональны.
Представим выражение (5.1) в малых приращениях:
![]() .
.
Это выражение скалярно умножим на
![]() :
:
![]() . (5.4)
. (5.4)
Для оценки устойчивости собственных значений в формуле (5.4) положим i = j :
![]() .
.
Поскольку
![]() ,
,
получаем
![]() ,
,
![]() .
.
Отсюда следует оценка
![]() .
.
Величина
![]()
называется коэффициентом перекоса;
![]() - угол между векторами
- угол между векторами
![]() .
.
Далее будем предполагать, что матрица
A симметрична1,
то есть
![]() ,
и все ее собственные числа различны. В
этом случае собственные векторы матрицы
А образуют в
,
и все ее собственные числа различны. В
этом случае собственные векторы матрицы
А образуют в
![]() полную ортонормированную систему,
которую можно использовать в качестве
базиса. Очевидно, что для симметричных
матриц
полную ортонормированную систему,
которую можно использовать в качестве
базиса. Очевидно, что для симметричных
матриц
![]() .
А значит, имеет место устойчивость
собственных значений:
.
А значит, имеет место устойчивость
собственных значений:
![]() .
.
Для оценки устойчивости собственных
векторов теперь рассмотрим случай
![]() .
В силу формулы (5.3) следует
.
В силу формулы (5.3) следует
![]() .
.
Используя это выражение и условие ортогональности векторов
![]() ,
,
из соотношения (5.4) получаем
![]() ,
,
![]() .
.
Разложим вектор
![]() по базису
по базису
![]() :
:
![]() .
.
Вычислим скалярное произведение
 ,
,
которое позволяет получить выражение
для коэффициентов разложения
![]() :
:
 .
.
В случае i = p за счет произвола в выборе
длины собственных векторов можно
положить
![]() .
Теперь разложение вектора
.
Теперь разложение вектора
![]() по базису
по базису
![]() имеет вид
имеет вид
 .
.
Оценим приращение вектора :
![]() ,
,
![]() .
.
Отсюда очевидно, что неустойчивость
собственных векторов имеет место в
случае, когда велики коэффициенты
перекоса
![]() ,
либо близки собственные значения
,
либо близки собственные значения
![]() .
.
Пример 5.2. Рассмотрим матрицу A,
указанную в примере 5.1. Нетрудно убедиться,
что для транспонированной матрицы
![]() собственные числа остаются теми же,
собственные числа остаются теми же,
![]() ,
а соответствующие собственные векторы
определяются следующим образом:
,
а соответствующие собственные векторы
определяются следующим образом:
![]() ,
,
![]() .
.
Перемножим скалярно собственные векторы обеих матриц:
![]() ,
,
![]() ,
,
то есть имеет место ортогональность собственных векторов матриц A и ;
![]() ,
,
![]() .
.
Подсчитаем коэффициенты перекоса:
 ,
,
 .
.
Пример 5.3. Оценить влияние погрешности на результаты вычисления собственных значений матрицы
 ,
,
где - малое возмущение (погрешность).
Решение характеристического уравнения
![]() .
.
дает корни (собственные значения):
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
В табл. 5.1 приведены собственные значения исходной матрицы при различных величинах .
Таблица 5.1
Определение собственных значений матрицы при заданных величинах погрешности
-
Собственные значения
= 0
= 0,1
= 0,01
= 0,001
1
1,0
0,983817673
0,9983384
0,999833384
2
2,0
2,051456633
2,005012689
2,000500125
3
3,0
2,948543367
2,994987311
2,999499875
4
4,0
4,016182327
4,0016616
4,000166616
