7.3. Точність, яка забезпечує задану достовірність

У попередніх підрозділах були розглянуті дві задачі, пов’язані з достовірністю контролю і точністю АСК:

1) оцінювання показників інструментальної достовірності контролю за відомими характеристиками параметрів об’єкта та відомими похибками каналів контролю АСК;

2) оцінювання точності каналів контролю за відомими похибками функціональних пристроїв, що входять до складу каналів.

Обидві задачі по суті своїй є задачами аналізу якості АСК як інструмента контролю. Вони дають відповідь на запитання, чи задовольняє спроектований засіб контролю за своїми точнісними характеристиками задані вимоги щодо достовірності контролю. А якщо – ні? Тоді виникає ще одна задача, обернена по відношенню до перших двох – задача синтезу, а саме: які характеристики точності повинні мати канали контролю, щоб задовольнити вимоги щодо достовірності контролю.

Постановка задачі

Універсальним критерієм того, що АСК забезпечує достатній рівень достовірності, є умова неперевищення ризиком виробника та ризиком замовника допустимих значень ризиків А_д і В_д при фіксованій імовірності Q браку об’єкта по сукупності контрольованих параметрів або при імовірності браку по кожному параметру об’єкта:

А ≤ А_д

В ≤ В_д (7.24)

при або ,

де N – кількість контрольованих параметрів об’єкта,

– апріорна ймовірність браку по і-му параметру об’єкта контролю.

Допустимі значення ризиків А_д і В_д встановлюють на основі тактико-технічних та (або) техніко-економічних вимог.

Наприклад, для однієї з наземних АСК, що контролює об’єкт з кількістю параметрів до однієї сотні, допустимі значення ризиків встановлені такими: А_д=0,02, В_д=0,01 при ймовірності браку об’єкта Q=0,1.

Як правило, об’єкт розробляється одночасно з засобами його контролю, коли інформації про закони розподілення параметрів та похибок їх контролю ще немає. Щоб вийти з цього положення, припускають, що контрольовані параметри незалежні між собою, розподілені за нормальним законом та рівнозначні щодо їх ролі у формуванні сумарних ризиків А і В та ймовірності Q. Умови рівнозначності можна записати так:

, (7.25)

, (7.26)

, (7.27)

,

де – коефіцієнт несиметрії допуску і-го параметра;

– імовірність браку об’єкта по і-му параметру;

– ризики виробника і замовника відповідно при контролі і-го параметра.

Імовірність Q браку об’єкта виражається через відповідні ймовірності браку по його параметрах. Згідно з формулою (7.13) маємо:

Урахувавши умову (7.25), перепишемо останнє рівняння таким чином:

,

звідки (7.28)

Наприклад, при N==100 і Q=0,1 обчислене за формулою (7.28) значення .

Нормований допуск параметра

З іншого боку, величину можна визначити, взявши інтеграл від функції розподілення параметра поза межами його допускової області – дивись формулу (7.2) і рис. 7.3:

(7.29)

де – щільність розподілення параметра ;

– нижня і верхня межі допуску і-го параметра.

7

Рис. 7.3. Нижній і верхній допуски параметра

Допущення про розподілення параметрів за нормальним законом дає змогу скористатися з добре розробленого математичного апарата так званих табульованих функцій.

Конкретизуємо функцію у виразі (7.29), записавши її як функцію нормального розподілення: (7.30)

де та – математичне сподівання та середнє квадратичне відхилення параметра , розподіленого за нормальним законом.

Співвідношення у формулі (7.30) має сенс центрованого відносно математичного сподівання, нормованого, безрозмірного відхилення параметра . Ним зручно користуватися незалежно від фізичної суті або розмірності параметра. Позначимо це співвідношення аргументом :

Введення аргументу означає перенесення точки відліку значень параметра в точку математичного сподівання, відносно якої відраховується нижній і верхній допуски параметра. Співвідношення між ними визначає коефіцієнт несиметрії допуску:

Один з допусків, більший за абсолютним значенням ( або ) служить для утворення нормованого допуску :

, (7.31)

менший із допусків служить для утворення нормованого допуску :

(7.32)

Згідно з теорією ймовірностей, потрапляння випадкової величини Y, що розподілена за нормальним законом, в інтервал , характеризується ймовірністю

(7.33)

де – нормована функція Лапласа, значення якої табульовані, тобто розраховані й зведені в табличні дані;

i – математичне сподівання та середнє квадратичне відхилення випадкової величини Y .

Застосовуючи формулу (7.33) до рівняння (7.29), другий член якого виражає ймовірність потрапляння значень параметра в інтервал одержимо:

(7.34)

Оскільки , змінимо знак аргумента в останньому члені формули (7.34) з одночасною зміною знака функції:

І нарешті, замінивши аргументи відповідно до рівнянь (7.31), (7.32), отримуємо:

(7.35)

Якщо допуск симетричний , формула (7.35) спрощується:

(7.36)

Отже, якщо формула (7.28) дає можливість обчислити ймовірність браку об’єкта по окремому і-му параметру, то формули (7.35), (7.36) дають можливість за вже знайденим значенням знайти відповідне йому значення нормованого допуску параметра.

Наприклад, для знайденого раніше за формулою (7.28) значення імовірності браку об’єкта по і-му параметру обчислюємо за формулою (7.36) значення за яким у таблиці значень нормованої функції Лапласа знаходимо відповідне значення аргумента .

Отже, попереднє значення допуску на параметр, яке задовольняє вихідні вимоги, встановлено (щоправда, в неявному, нормованому вигляді).

Визначення ризиків при контролі одного, окремо взятого параметра

Далі визначимо допустимі значення ризиків і при контролі окремого і-го параметра.

Відповідно до формули (7.18) і умов щодо обмежень (7.24) запишемо:

З урахуванням умов рівнозначності (7.25), (7.26) маємо:

або, враховуючи вираз (7.28),

,

звідки а отже,

(7.37)

де – гранично допустима межа ризику виробника при контролі і-го параметра.

За даними нашого прикладу при маємо:

Отже, для умов нашого прикладу ризик не повинен перевищувати величину

Аналогічно для визначення допустимого значення , керуючись формулою (7.19) та обмеженнями (7.24), запишемо:

або, враховуючи умови рівнозначності (7.25) – (7.27),

(7.38)

Останній член у виразі (7.38) згідно з формулою (7.19) є показником достовірності Г, який відповідно до графа ймовірностей подій (дивись рис. 7.1) виражається через імовірність (1-Q) та ризик виробника А.

Отже, (7.39)

Підставимо вираз (7.39) у формулу (7.38), взявши :

Розв’язуючи цю нерівність відносно та враховуючи рівняння (7.37), одержимо:

За даними нашого прикладу (при N==100, Q=0,1 і ) маємо:

Отже, ризик не повинен перевищувати величину

Визначення допустимої похибки контролю параметра

Визначивши величини знайдемо тепер допустиме значення похибки контролю і-го параметра, яке забезпечує виконання допустимих значень та .

Згідно з формулою (7.22) ризик виробника за і-им параметром:

, (7.40)

де – функція розподілення похибки каналів контролю параметра .

Вважаючи параметр і похибку незалежними одне від одного та розподіленими за нормальними законами, запишемо формулу (7.40) у такому вигляді:

, (7.41)

де та – математичне сподівання та середня квадратична похибка каналів контролю і-го параметра, іншими словами – систематична та середня квадратична складові похибки .

Уведемо новий аргумент

, (7.42)

який має смисл нормованої середньої квадратичної похибки, а також аргумент , що має сенс центрованої відносної похибки. Перепишемо вираз (7.41) з урахуванням уведених аргументів, замінивши межі інтегрування відповідними нормованими величинами, а диференціали – їх відповідниками: на , на .

Після скорочень та спрощень одержимо:

(7.43)

Аналогічно, на основі рівняння (7.23) та заміни відповідних аргументів отримаємо рівняння для ризику замовника:

(7.44)

Рівняння (7.43) та (7.44) являють собою двовимірні інтеграли ймовірностей типу , які безпосереднім інтегруванням, через елементарні функції не виражаються. Але їх можна знайти за допомогою табульованих функцій, чисельним інтегруванням на комп’ютері за спеціальними програмами або шляхом заміни їх спрощеними апроксимуючими функціями. Скористаймось таблицями обчислених характеристик апроксимуючих функцій, наведених у праці 12:

(7.45)

де – екстремум, математичне сподівання та середнє квадратичне відхилення апроксимуючих функцій.

Оскільки таблиця обчислених значень не дає можливості безпосереднього визначення допустимої похибки внаслідок дискретності її значень, доводиться застосовувати метод послідовних наближень. Для цього обчислюють спочатку два пробні значення та за формулами:

, (при ).

За знайденими величинами за допомогою таблиці знаходять методом інтерполяції два відповідні значення і , за якими обчислюють величину першого наближення:

(7.46)

де –значення , обчислені за формулою (7.45).

Далі обчислюють за формулою (7.45) значення . Якщо воно суттєво відрізняється від , процес продовжують, обчислюючи значення другого наближення:

(7.47)

За одержаним знову обчислюють значення і порівнюють його з і так далі, допоки обчислене значення не буде відрізнятися від більше, ніж встановлено заданою точністю наближення, наприклад, не більше 1%.

Проведемо відповідні розрахунки для нашого прикладу ( =0,000225; ; )

Результати інтерполяції за табличними даними 12, с.143  в графі :

Далі обчислюємо:

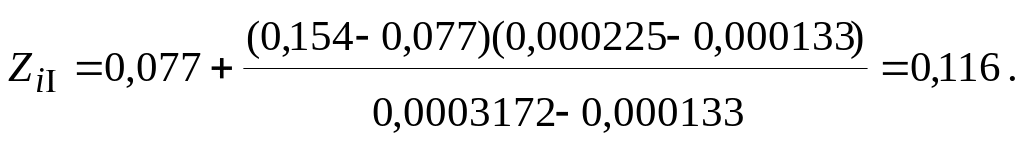
Для обчисленого =0,116, інтерполюючи, знаходимо за допомогою таблиці решту даних, що відповідають цьому значенню, і обчислюємо значення ризику першого наближення:

Похибка наближення 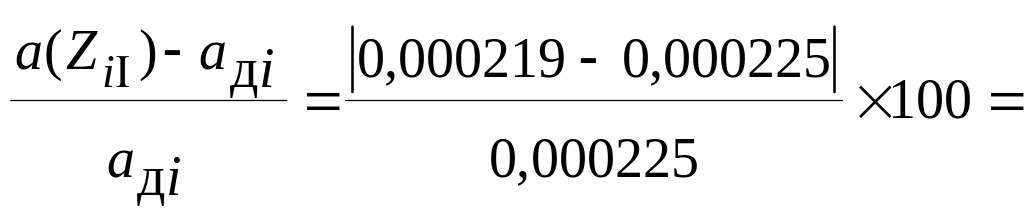2,7% перевищує задану (1%), тому процес наближення продовжується:

Знову за допомогою таблиці знаходимо і обчислюємо значення ризику другого наближення:

Похибка другого наближення 0,44% не перевищує задану, тому розв’язком задачі є

Аналогічні обчислення проводять для того, щоб знайти гранично допустиму похибку , що забезпечує допустимий ризик замовника . Для цього обчислюють спочатку два пробні значення та за формулами:

(при ),

а далі виконують операції послідовних наближень за формулами (7.46), (7.47), у яких аргумент замінюють аргументом .

Результат обчислень для вихідних значень: ( =0,0001129; ; ) такий:

(похибка наближення менша від 0,1%).

Отже, для умов цього прикладу вимога щодо забезпечення ризику замовника виявилась більш жорсткою, ніж вимога щодо ризику виробника: . Тому для подальших розрахунків потрібно взяти:

Тепер можна перейти до обчислення конкретних похибок контролю і-го параметра.

Згідно з формулою (7.42) середня квадратична похибка:

(7.48)

Другий співмножник у виразі (7.48) можна знайти, записавши очевидне рівняння (дивись рис.7.3):

.

Поділивши обидві частини рівняння на , отримаємо:

,

звідки . (7.49)

Підставивши формулу (7.49) у рівняння (7.48), одержимо формулу для визначення похибки контролю параметра із двостороннім допуском:

.

Для параметрів з одностороннім допуском:

.

І нарешті, обчислюють граничні значення допустимої абсолютної похибки за формулою:

.

Наприклад, для ;

і

=

Ч а с т и н а 2