5.3. Биномиальное распределение

Запишем формулу Бернулли:

Данная формула является аналитическим выражением искомого закона распределения.

Определение. Биномиальным называют распределение вероятностей, определяемое формулой Бернулли. Закон назван «биномиальным»потому, что правую часть (*) можно рассматривать как общий член разложения бинома Ньютона:

Табличная запись биномиального закона:

Х	n	n – 1	…	k	…	0
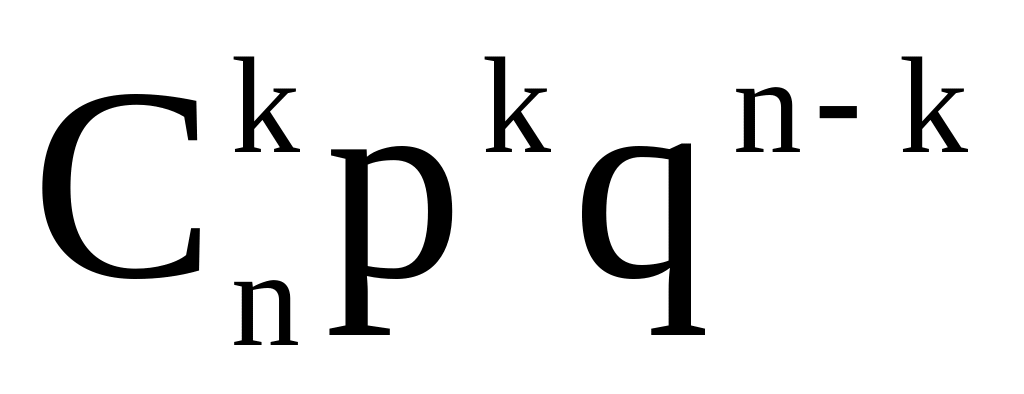
р	pn	npn-1q	…		…	qn

Пример. Монета брошена 2 раза. Написать в виде таблицы закон распределения случайной величины Х – числа выпадений «герба».

Решение. - вероятность появления «герба»в каждом бросании;

- вероятность непоявления «герба» в каждом бросании.

При двух бросаниях монеты «герб» может появиться либо 2 раза, либо 1 раз; либо совсем не появится. таким образом, возможные значения Х таковы:

х₁ = 2; х₂ = 1; х₃ = 0.

Установим вероятность этих значений:

Контроль: 0,25 + 0,5 + 0,25 = 1.

5.4. Распределение Пуассона

Установим вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность события очень мала, а событие наступит ровно k раз (р  0,1).

Пусть np = λ – т.е. сохраняет постоянное значение. Воспользовавшись формулой Бернулли, свойствами предела, вторым замечательным пределом, получаем:

Указанная формула выражает закон распределения Пуассона вероятностей массовых (n велико) и редких (р мало) событий.

Пример. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0002. Определить вероятность того, что на базу прибудут три негодных изделия.

Решение. n = 5000; p = 0,0002; k = 3.

λ = np = 5000 ∙ 0,0002 = 1

5.5. Геометрическое распределение

Пусть в первых k – 1 испытаниях событие А не наступило, а k – м испытании появилось. Вероятность этого «сложного события», по теореме умножения вероятностей независимых событий:

Полагая k = 1, 2, … в (*) получим:

p, qp, q²p, …, q^k-1 ∙ p, … (**)

Получили геометрическую прогрессию с первым членом р и знаменателем q (0 < q <1).

По этой причине распределение (*) называют геометрическим.

Из курса числовых рядов известно, что ряд (**) сходится и его сумма равна единице.

Пример. Из орудия производится стрельба по мишени до первого попадания. Вероятность попадания в цель р = 0,6. Определить вероятность того, что попадание произойдет при третьем выстреле.

Решение. р = 0,6; q = 0,4; k = 3.

Р(3) = q^k-1 ∙ p = 0,4² ∙ 0,6 = 0,096.

§ 6. Математическое ожидание дискретной случайной величины

6.1. Числовые характеристики дискретных случайных величин

Закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями. Иногда даже выгоднее пользоваться числами, которые описывают случайную величину суммарно; такие числа называют числовыми характеристиками случайной величины.

К числу важных числовых характеристик относится математическое ожидание.

Определение. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.

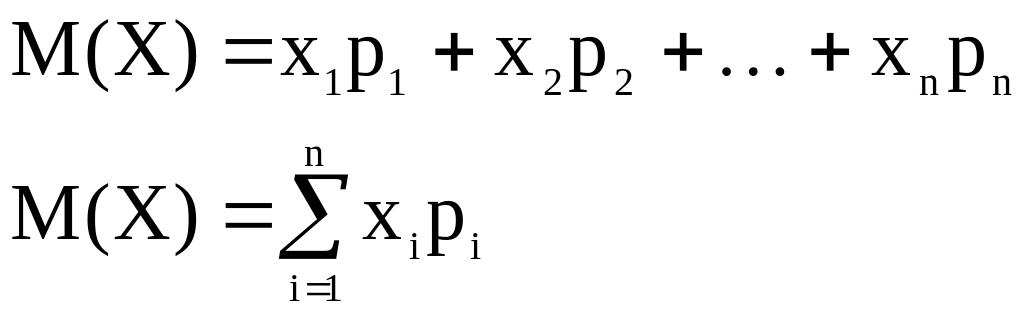
Примечание. 1. Математическое ожидание дискретной случайной величины есть неслучайная (постоянная) величина.

2. Математическое ожидание числа появлений события в одном испытании равно вероятности этого события.

3. Вероятностный смысл математического ожидания: математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины.

Пример. Определить М(Х), зная закон ее распределения:

Х	3	5	2
р	0,1	0,6	0,3

Решение.