§ 9. Плотность распределения вероятностей непрерывной случайной величины

9.1. Основные понятия

Определение. Плотностью распределения вероятностей непрерывной случайной величины Х называют функцию f(x) – первую производную от функции распределения F(x):

f(x) = F’(x)

F(x) – первообразная для f(x).

Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a; b), равна определенному интегралу от плотности распределения, взятому в пределах от а до b:

Пример. Определить функцию распределения по данной плотности распределения:

Решение.

Если х ≤ а, то f(x) = 0, поэтому F(x) = 0,

если a < x ≤ b, то .

Рис.3.

9.2. Свойства плотности распределения

1. Плотность распределения – неотрицательная функция, т.е. f(x) ≥ 0.

2. Несобственный интеграл от плотности распределения в пределах от - до +  равен единице, т.е.

Пример.

, определить а, если f(x) – плотность распределения.

Решение.

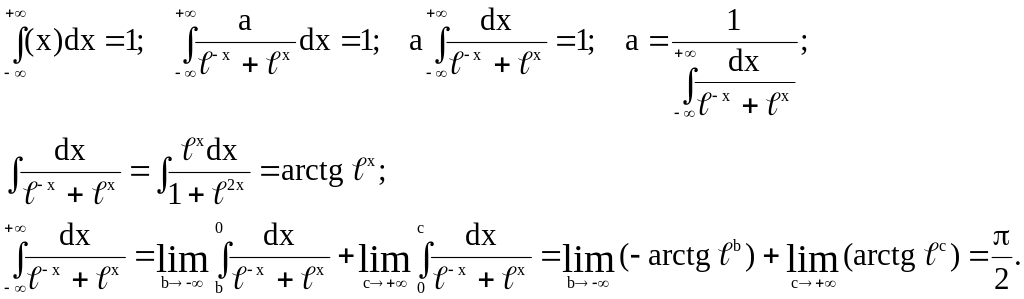
Таким образом

Определение. Плотности распределений непрерывных случайных величин называют законами распределений.

Определение. Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет свое постоянное значение.

Вычислим плотность равномерного распределения f(х), считая что все возможные значения случайной величины заключены в интервале (a; b), на котором функция f(х) сохраняет постоянные значения.

По условию Х не принимает значений вне (a; b), поэтому f(х) = 0 при х <а, х > b. Вычислим постоянную С:

Р ис.4.

§ 10. Нормальное распределение

10.1. Числовые характеристики непрерывных случайных величин

Определение. Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a; b], называют определенный интеграл:

Если возможные значения принадлежат всей оси ОХ, то:

Определение. Дисперсией непрерывной случайной величины Х называют математическое ожидание квадрата ее отклонения.

Если Х  [a; b], то

если X  (-; +), то

Определение. Среднее квадратическое отклонение непрерывной случайной величины определяется, как и для величины дискретной, равенством:

Примечания. 1. Свойства математического ожидания и дисперсии дискретных случайных величин сохраняются и для непрерывных величин;

2.

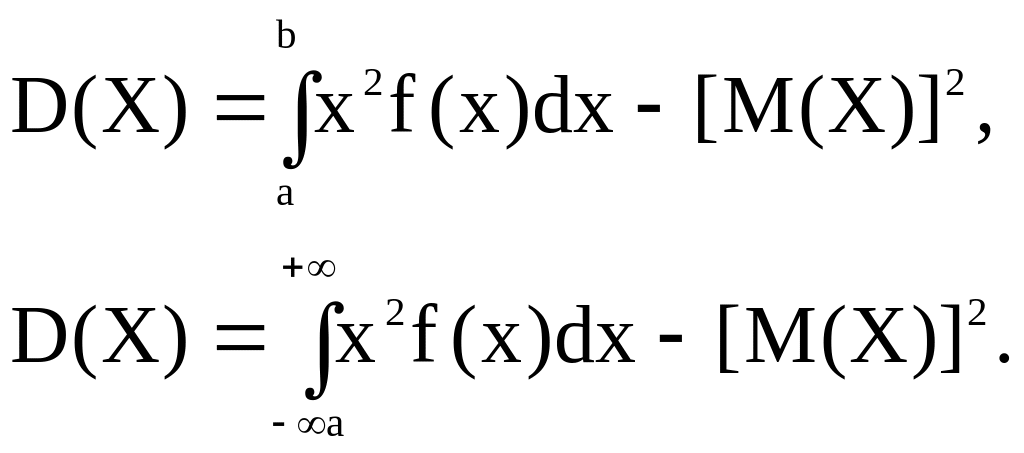
Пример.

Решение.

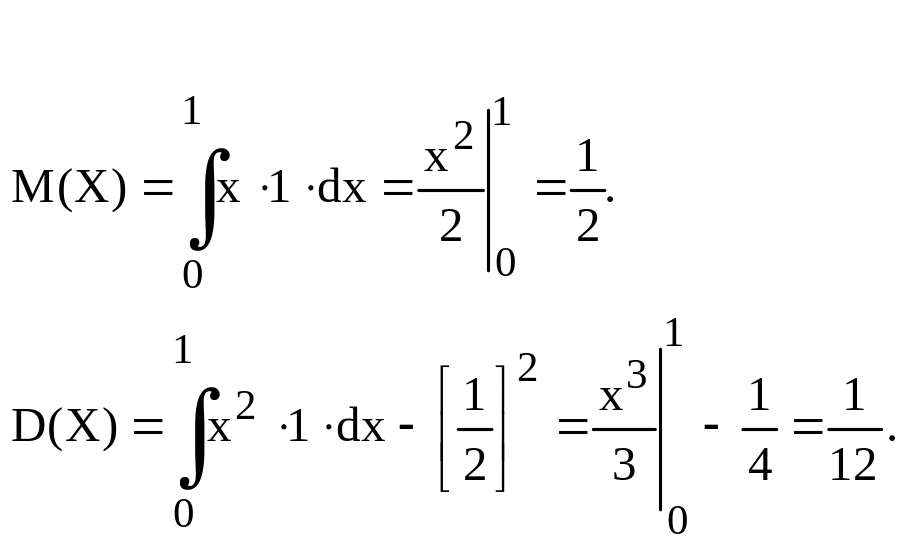
10.2. Нормальное распределение

Определение. Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью:

Примечания.

1. 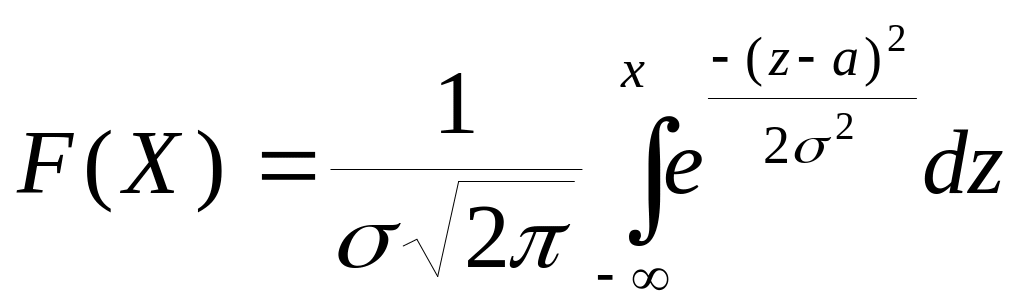- функция общего нормального распределения;

- функция нормированного распределения.

2. Вероятность попадания нормированной нормальной величины Х в интервале (0; х) можно установить, пользуясь функцией Лапласа:

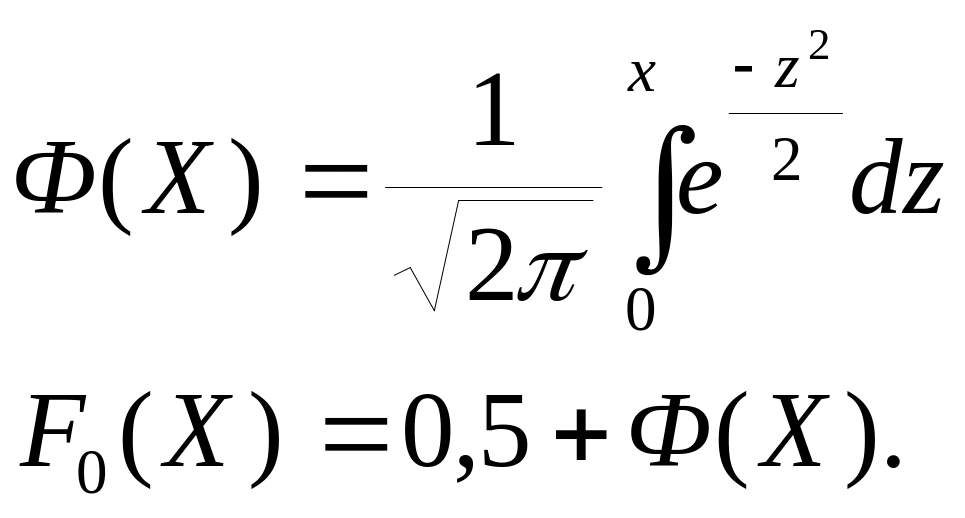
10.3. Нормальная кривая

Определение. График плотности нормального распределения называют нормальной кривой (кривой Гаусса).

1. Функция определена на всей числовой оси х.

2. При всех х функция принимает положительные значения.

3. При , т.е. ОХ – горизонтальная асимптота.

4.

5. График симметричен относительно прямой x = a.

6.

При переходе через эти точки вторая производная меняет знак, следовательно:

Рис.5.

Изменение величины параметра а не изменяет формы нормальной кривой, а приводит лишь к ее сдвигу:

- вправо, если а возрастает;

- влево, если а убывает.

С возрастанием σ максимальная ордината нормальной кривой убывает, а кривая становится более пологой, при убывании – ордината возрастает в положительном направлении оси Оу, кривая становится «островершинной».