7.3. Свойства дисперсии

1. Дисперсия постоянной величины С равна нулю: D(С) = 0.

2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: D(СХ) = С²D(Х).

3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин: D(X + Y) = D(Х) + D(Y).

Следствия.

1.

2.

4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:

Теорема. Дисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании: D(X) = npq.

7.4. Среднее квадратическое отклонение

Определение. Средним квадратическим отклонением случайной величины Х называют квадратный корень из дисперсии:

В тех случаях, когда желательно, чтобы оценка рассеяния имела размерность случайной величины, вычисляют среднее квадратическое отклонение, а не дисперсию.

Пример. Случайная величина Х задана:

X	2	3	10
р	0,1	0,4	0,5

Вычислить σ(Х) - ?

Решение.

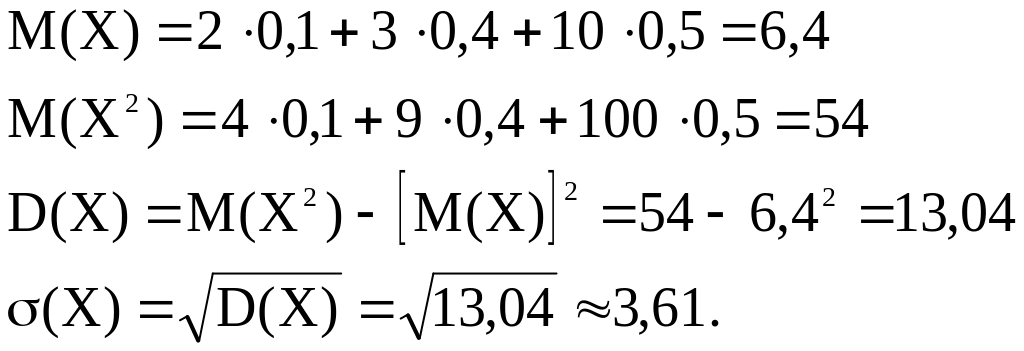
Теорема. Среднее квадратическое отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин:

Рассмотрим три положения, которые устанавливают связь между числовыми характеристиками среднего арифметического случайной величины и соответствующими характеристиками каждой отдельной величины.

1. Математическое ожидание среднего арифметического одинакого распределенных взаимно независимых случайных величин равно математическому ожиданию а каждой из величин: .

2. Дисперсия среднего арифметического n одинаково распределенных взаимно независимых случайных величин в n раз меньше дисперсии каждой из величин:

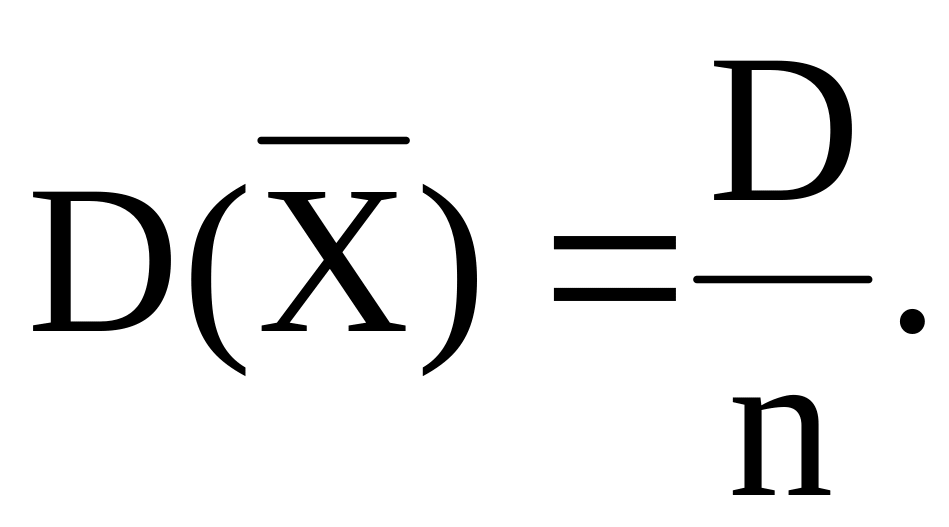
3. Среднее квадратическое отклонение среднего арифметического nодинаково распределенных взаимно независимых случайных величин в 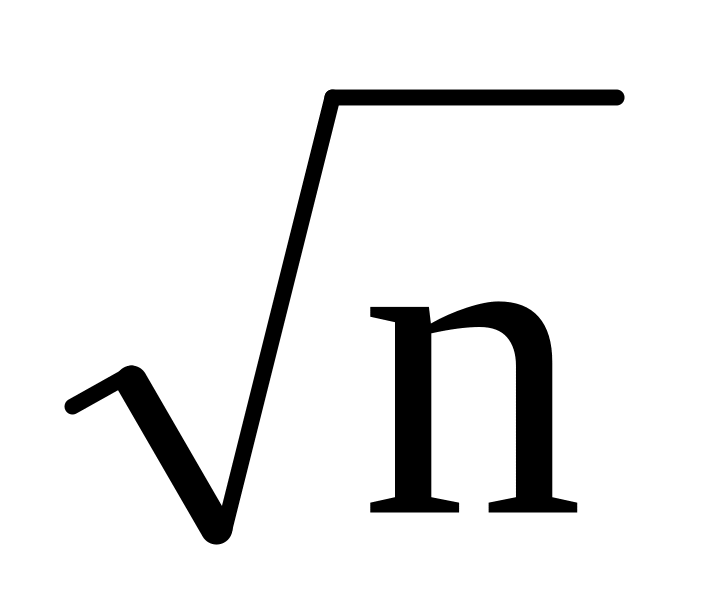раз меньше среднего квадратического отклонения каждой из величин:

§ 8. Функция распределения вероятностей случайной величины

8.1. Основные понятия

Определение. Функцией распределения называют Функцию F(Х), определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х, т.е. F(X) = P(X < x).

Геометрически: F(X) есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х. F(X) – интегральная функция.

Определение. Случайную величину называют непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.

8.2. Свойства функции распределения

1. Значение функции распределения принадлежат отрезку [0; 1], т.е.

2. F(X) – неубывающая функция, т.е. если x₂ > x₁, то F(X₂) ≥ F(X₁).

Следствия. 1. Вероятность того, что случайная величина примет значение, заключенное в интервале (a; b), равна приращению функции распределения на этом интервале: P(a ≤ X < b) = F(b) – F(a).

2. Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю.

3. Если возможные значения случайной величины принадлежат интервалу (a; b), то:

1. F(X) = 0, при х ≤ а;

2. F(X) = 1, при х ≥ b.

Следствие. Если возможные значения непрерывной случайной величины расположены на всей оси Х, то справедливы следующие предельные отношения

Рассмотренные выше свойства позволяют представить, как выглядит график функции распределения непрерывной случайной величины:

1. График расположен в полосе, ограниченной прямыми: у = 0, у = 1 (свойство 1).

2. При возрастании х  (a; b), график «поднимается вверх» (свойство 2).

3. При х ≤ а ординаты равны нулю; при х ≥ b ординаты графика равны единице (свойство 3).

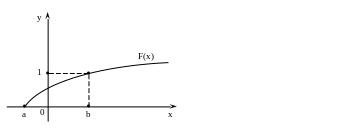
Рис.1.

Пример. Известен закон распределения:

X	1	4	8
р	0,3	0,1	0,6

Определить функцию распределения и вычертить ее график.

Решение. При x ≤ 1, F(x) = 0 (свойство 3);

при 1 < x ≤ 4, F(x) = 0,3;

при 4 < x ≤ 8, F(x) = 0,4.

Действительно, при 4 < x₁ ≤ 8, F(x₁) равно вероятности события Х < х₁, которое может быть осуществлено, когда Х примет значение 1 (Р(Х) = 0,3) или значение 4 (Р(Х) = 0,1). Поскольку эти два события несовместны, то по теореме сложения вероятностей вероятность события Х < х₁ равна сумме: 0,3 + 0,1 = 0,4.

При х > 8, F(x) = 1.

Таким образом,

Р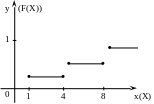 ис.2.