Глава 1. Элементы математической статистики

§ 1. Выборочный метод. Точечные оценки

1. Генеральная и выборочная совокупности. В теории вероятностей обычно решаются задачи, связанные со случайными величинами, для которых заданы закон распределения или функция распределения. Исходя из этого, подсчитываются характеристики случайных величин и вероятности того, что их значения окажутся на том или ином промежутке. На практике положение оказывается совсем другим. С помощью различных подсчетов или по показаниям приборов мы получаем лишь некоторые (обычно приближенные) значения случайной величины, по которым приходится устанавливать ее всевозможные характеристики и, в частности, закон или функцию распределения.

Пример 1. Проводится тестирование по математике студентов технических специальностей университета. Для этого из разных групп произвольно выбирают 200 студентов, которые отвечают на предложенные вопросы. Затем составляется таблица результатов тестирования по десятибалльной шкале, например, такая.

Оценка	1	2	3	4	5	6	7	8	9	10
Количество	3	7	18	25	40	45	30	17	10	5

Пример 2. Изготовлена партия шариков для подшипников в количестве 5000 штук. Для контроля отбирают 200 шариков и измеряют их диаметр. Если требуемый диаметр равен 2 мм, то может быть получена, например, такая таблица результатов.

Диаметр	1,97	1,98	1,99	2,00	2,01	2,02	2,03
Количество	20	20	40	50	40	20	10

Заметим, что проверка всей партии контролируемых объектов (сплошной контроль) обычно по разным причинам невозможна: например, объектов слишком много или проверка приводит к разрушению объекта (испытание детали на прочность).

Поэтому из множества исследуемых объектов отбирается для контроля некоторая часть, которую называют выборочной совокупностью. Число элементов выборочной совокупности называют ее объемом. Все множество исследуемых объектов называют генеральной совокупностью, а число элементов этого множества – объемом генеральной совокупности.

Так, во втором из рассмотренных примеров имеем: объем генеральной совокупности равен 5000, объем выборочной совокупности равен 200.

2. Выборка и вариационная последовательность. Эмпирический закон распределения. Пусть в результате n независимых испытаний получены последовательно следующие значения некоторой случайной величины :

. (1)

Эту последовательность называют статистической последовательностью или выборкой значений , а число n – объемом выборки. Располагая все различные числа выборки (1) в порядке возрастания, получаем конечную последовательность

, (2)

которую называют вариационной. Члены вариационной последовательности называют вариантами. Число R  z_m – z₁ (разность между наибольшей и наименьшей вариантами) называют размахом вариационной последовательности или размахом варьирования. Число, делящее вариационную последовательность на две части, равные по числу вариант, называют выборочной медианой. Если m  2k + 1, то выборочная медиана есть варианта z_k+1; при m  2k за выборочную медиану принимают обычно число .

Пример. Для выборки –3, 2, –1, –3, 5, –3, 2 вариационная последовательность есть –3, –1, 2, 5; размах варьирования R  5 – (–3)  8; выборочная медиана  0,5.

Если число испытаний n достаточно велико, то можно предполагать, что будут получены все значения случайной величины , вероятности которых не слишком близки к нулю. Пусть n_j – число испытаний, в которых получено значение z_j. Составим таблицу, в первой строке которой запишем варианты (2), а во второй – частоты этих чисел.

z1	z2	z3	...	zm
			...

Эта таблица задает закон распределения, который называют эмпирическим законом распределения случайной величины  ¹.

Так, случайная величина из примера 1 п. 1 есть оценка за контрольную работу. Разделив все числа 2-й строки приведенной в примере таблицы на n  200, получаем таблицу для эмпирического закона распределения этой случайной величины.

1	2	3	4	5	6	7	8	9	10
0,015	0,035	0,09	0,125	0,2	0,225	0,15	0,085	0,05	0,025

Варианту, имеющую наибольшую частоту, называют модой эмпирического распределения. В приведенном примере мода эмпирического распределения равна 6.

3. Эмпирическая функция распределения. Гистограм­ма и полигон частот. Если случайная величина  непрерывна, то вероятность появления любого ее значения равна нулю, поэтому получающаяся для нее выборка значений (1), как правило, не будет содержать повторений и, следовательно, все частоты в таблице ее эмпирического закона распределения будут равны 1/n. Такая таблица плохо характеризует случайную величину, поэтому для непрерывной случайной величины предпочтительнее рассматривать эмпирическую функцию распределения, которую получают следующим образом.

Пусть x – любое действительное число, k_x – количество чисел x_j в выборке (1), удовлетворяющих неравенству x_j < x. Отношение k_x / n есть частота появления события ( < x), которую можно принять за эмпирическую вероятность этого события. Функция является эмпирической функцией распределения для случайной величины .

Если, например,  – случайная величина из примера 2 п. 1 (диаметр шарика), то n  200,

График полученной функции изображен на рис. 7.

Кроме эмпирической функции распределения бывает полезно построить аналог плотности вероятностей. Для этогоотрезок [z₁; z_m], концами которого являются наименьшая и наибольшая варианты, разбивают на частичные отрезки обычно одной и той же длины h. На j‑том частичном отрезке строится прямоугольник, высота которого равна n_j / nh, где n_j – количество чисел статистической последовательности (1), попавших в этот отрезок¹. Фигура, составленная из построенных прямоугольников, называется гистограммой частот² для выборки (1). Так как площадь j‑го прямоугольника равна, очевидно, n_j / n, площадь всей фигуры равна сумме частот n_j / n, т. е. единице.

Пример 1. Пусть получены следующие результаты наблюдений.

Варианты	– 2	0	1	2	3	5	7
Количество в выборке	4	5	7	8	6	2	1

Построим гистограмму для этого распределения. Здесь n  33, наименьшая и наибольшая варианты соответственно –2 и 7, длина отрезка [– 2; 7] равна 9. Разобьем его на 4 отрезка длины h  9 : 4  2,25. Имеем:

Отрезок	[–2; 0,25]	[0,25; 2,5]	[2,5; 4,75]	[4,75; 7]
kj	9	15	6	3
kj / nh	0,12	0,20	0,08	0,04

Г истограмма частот для этого распределения изображена на рис. 8.

На практике вы-соту j‑го прямоугольника часто берут равной числу n_j / h. В этом случае площадь j‑го прямоугольника равна n_j, а следовательно, площадь всей фигуры равна n, т. е. объему выборки.

В некоторых слу-чаях достаточно наглядным является более простой способ изображения полученного в результате наблюдения распределения частот. При этом способе для каждого числа z_j вариационной последовательности (2) на координатной плоскости строится точка (z_j, n_j / n), где n_j  – число повторений варианты z_j в выборке (1). Соединяя последовательно эти точки отрезками, получим ломаную, которая называется полигоном частот.

Вместо частот n_j / n в качестве 2-й координаты часто берут n_j (в этом случае ломаная не так сильно прижимается к оси абсцисс).

Пример 2. Пусть результатом испытаний является следующая выборка: – 3; + 2; –1; – 3; + 5; – 3; + 2. Тогда получаем: z₁  –3, k₁  3;

z ₂  –1, k₂  1; z₃  2, k₃  2; z₄  5, k₄  1.

Соединяя отрезками точки (z_j, k_j), получаем полигон частот, изображенный на рис. 9.

4. Эмпирическое математическое ожидание и эмпирическая дисперсия. Самыми важными характеристиками случайной величины  являются математическое ожидание M и дисперсия D. Поэтому возникает задача нахождения этих величин по тем значениям x₁, x₂, ..., x_n, которые были получены в результате наблюдений.

Оказывается, что достаточно хорошим приближением для математического ожидания является среднее арифметическое

, (3)

которое называют эмпирическим или выборочным математическим ожиданием.

Заметим, что есть математическое ожидание случайной величины, распределенной по эмпирическому закону, который получается, если пренебречь не появившимися в результате наблюдений значениями (как маловероятными), а за вероятности появившихся значений принять их частоты (см. первую таблицу на стр. 39). Действительно, поскольку x₁  x₂  …  x_n  n₁z₁  n₂z₂  …  n_m z_m, получаем

.

В качестве приближенного значения для дисперсии естественно взять дисперсию случайной величины, распределенной по эмпирическому закону. Ее называют эмпирической или выборочной дисперсией. Обозначая выборочную дисперсию через , получаем

. (4)

Квадратный корень из этого числа, т. е. число , называют выборочным квадратичным отклонением.

Обычно вместо величины предпочитают в качестве оценки дисперсии использовать величину

. (5)

Эту величину называют исправленной выборочной дисперсией. При достаточно больших n она почти не отличается от оценки (4) (поскольку ), однако оценка (5) обладает важным свойством несмещенности, которое устанавливается в доказываемой ниже теореме.

Пример. Контрольные измерения прочности бетона при сжатии дали следующие результаты (в Н/мм²): 43,4; 48,0; 46,1; 36,2; 45,3; 41,2. Используя формулы (3) и (5), получаем эмпирическое математическое ожидание и исправленную выборочную дисперсию прочности бетона при сжатии:

;

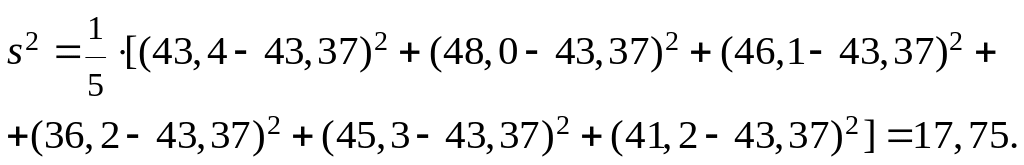
Наблюдаемые в эксперименте значения x_j случайной величины  сами являются случайными величинами и притом попарно независимыми (только от случая зависит, что в качестве j-го значения было зафиксировано число x_j, а не какое-нибудь другое). Эти случайные величины принимают те же значения и распределены так же, как и , поэтому Mx_j  M и Dx_j  D ( j  1, 2, …, n).

Отсюда следует, что и s² также являются случайными величинами. Справедлива следующая

Теорема. Имеют место равенства: (свойство несмещенности оценок и s²).

Доказательство. Первое равенство получается следующим образом: .

Для доказательства второго заметим, что для любой случайной величины  и, следовательно, . Используя этот результат, получаем

Заметим, что аналогичные подсчеты для величины дают меньшее значение , так что оценка не обладает свойством несмещенности.

Общее понятие несмещенности будет рассмотрено в п. 6.

5. Эмпирические моменты и эмпирические центральные моменты. Эмпирические асимметрия и эксцесс. В тех случаях, когда для характеристики случайной величины  приходится использовать моменты и центральные моменты, возникает задача определения этих чисел по значениям x₁, x₂, ..., x_n случайной величины , полученным в результате наблюдений. Как и в случаях эмпирического математического ожидания и эмпирической дисперсии, при построении требуемых оценок исходят из эмпирического закона распределения (см. первую таблицу на стр. 39).

Пусть – все различные числа из выборки x₁, x₂, ..., x_n, и n_j – число повторений в этой выборке варианты z_j. Эмпирической вероятностью варианты z_j является частота n_j / n, следовательно, момент k-го порядка случайной величины, распределенной по эмпирическому закону, есть

.

Среднее арифметическое k-х степеней значений x₁, x₂, ..., x_n случайной величины, полученных в результате наблюдений, называют эмпирическим моментом порядка k этой случайной величины.

Эмпирический момент k-го порядка будем обозначать . Таким образом,

. (6)

Сравнивая формулу (6) с формулой (3), получаем , т. е. эмпирический момент 1-го порядка есть эмпирическое математическое ожидание.

Эмпирическим центральным моментом порядка k случайной величины называют среднее арифметическое k-х степеней отклонений наблюдаемых значений случайной величины от эмпирического математического ожидания.

Обозначая эмпирический центральный момент k-го порядка через , имеем по определению

. (7)

Легко убедиться, что есть не что иное, как центральный момент случайной величины, распределенной по эмпирическому закону, так что выполняется равенство: . Сравнивая формулы (4) и (7), усматриваем, что , т. е. эмпирический центральный момент 2-го порядка равен эмпирической дисперсии.

Формулы, выражающие центральные моменты через моменты (Введение, § 2, п. 5), очевидно, остаются верными для эмпирических моментов, так что имеем:

, , , .

Выборочная асимметрия и выборочный эксцесс определяются соответственно как асимметрия и эксцесс эмпирического распределения, т. е. равенствами

, ,

где и – эмпирические моменты, а – выборочное квадратичное отклонение.

Выборочная асимметрия служит для характеристики несимметричности полигона частот. Если эмпирическое распределение имеет одну моду (такое распределение называют унимодальным), то асимметрия отрицательна, когда наблюдается пологий спуск слева от моды и более крутой спуск справа от моды, и положительна в противном случае.

Выборочный эксцесс служит для сравнения выборочного распределения с нормальным распределением. При отрицательном эксцессе соответствующий полигон является более пологим по сравнению с нормальной кривой. Если же эксцесс положителен, то полигон будет более крутым по сравнению с нормальной кривой.

6. Точечные оценки параметров. Несмещенность, эффективность и состоятельность. Пусть  – некоторый неизвестный параметр распределения случайной величины . Для нахождения этого параметра используется выборка (1) значений . Оказывается, что в некоторых случаях эти значения позволяют найти достаточно хорошие приближения неизвестного параметра. Всякое такое приближение называют точечной оценкой параметра .

Обозначим через _n какую-либо точечную оценку параметра , полученную в результате n испытаний. Эта оценка определяется выборкой значений , полученных в результате испытаний, так что _n = _n(x₁, x₂, ..., x_n). Поскольку x₁, x₂, ..., x_n – случайные величины, то и _n также является случайной величиной. Естественно ожидать, что математическое ожидание этой случайной величины совпадает со значением искомого параметра , т. е. выполняется равенство

. (8)

Точечная оценка, для которой выполняется условие (8), называется несмещенной.

Например, в п. 4 построены точечные оценки для математического ожидания M и s² для дисперсии D и доказаны равенства: , так что обе оцен­ки являются несмещенными.

Среди несмещенных оценок одного и того же параметра наиболее выгодной является, очевидно, такая, которая имеет наименьший разброс значений, т. к. в этом случае можно ожидать, что получающаяся в каждом случае конкретная оценка имеет минимальное отличие от точного значения искомого параметра. В связи с этим введем следующее определение.

Несмещенная точечная оценка данного параметра, име­ющая наименьшую дисперсию, называется эффективной.

Например, можно доказать, что в случае нормально распределенной случайной величины  рассмотренная выше несмещенная оценка для параметра M является эффективной.

Минимальное отличие эффективной оценки от значения искомого параметра может все же оказаться при фиксированном объеме выборки n достаточно большим, поэтому естественно требовать, чтобы оценка становилась более точной при неограниченном возрастании n. В связи с этим вводится следующее понятие.

Точечная оценка _n параметра  называется состоятельной, если для любого ε > 0 выполняется соотношение

.

Другими словами, оценка _n является состоятельной, если при достаточно больших n для любого ε > 0 практически достоверно неравенство , т. е. _n как угодно мало отличается от .

В качестве примера докажем состоятельность точечной оценки для M. Используем известное неравенство Чебышева . Поскольку и , получаем

.

Можно доказать, что при некоторых условиях эмпирические моменты и эмпирические центральные моменты являются состоятельными. В частности, точечные оценки и s² для дисперсии D являются состоятельными, если для  существуют моменты до 4-го порядка. Таким образом, формулы и дают при большой выборке приближенные значения математического ожидания и дисперсии с какой угодно точностью.