§ 2. Случайные величины

1. Определение и примеры. При проведении различных статистических экспериментов часто бывает интересен не исход эксперимента, а некоторая связанная с этим исходом числовая характеристика. В связи с этим возникает необходимость изучать числовые функции, определенные на множестве исходов данного эксперимента.

Пример 1. При стрельбе по мишени множество всевозможных исходов U есть некоторая часть плоскости, куда может попасть пуля. Каждой точке uU отвечает определ енное число очков, кото­рое мы обозначим через (u). Для стрелкá, очевидно, важно именно это число, а не сама точка, в которую попадет пуля. Например, для точек a и b, отмеченных на рис. 2, имеем (a)  (b)  2, так что при оценке результатов стрельбы эти точки не различаются.

Пример 2. Производится n независимых испытаний, в результате каждого из которых может появляться (или не появляться) событие А. Исходами здесь являются конечные последовательности u  (u₁, u₂, …, u_n), где u_k – исход k-го испытания. Пусть (u) – число появлений события А при исходе u (т. е. число тех u_k, которые благоприятны событию А). Тогда  – функция, определенная на множестве исходов данного эксперимента и принимающая значения 0, 1, 2, …, n.

Если  – числовая функция, определенная на множестве U всевозможных исходов статистического эксперимента, то значение этой функции (u) есть число, определяемое исходом u, полученным при проведении эксперимента, и, следовательно, зависящее от случая. При решении многих прикладных задач, приводящих к рассмотрению таких функций, оказывается важным установить вероятность того, что при проведении эксперимента значение (u) попадет в тот или иной числовой промежуток. Поэтому имеет смысл рассматривать лишь такие функции, для которых попадание значения в любой числовой промежуток I есть одно из событий, связанных с данным экспериментом. В этом случае множество {uU | (u)I} является множеством исходов, благоприятных этому событию. Сформулируем теперь основное для всего дальнейшего изложения

Определение 1. Случайной величиной на вероятностном пространстве (U, F, P) называется всякая функция , определенная на множестве U, принимающая действительные значения и такая, что для любого числового промежутка I имеет место соотношение {uU | (u)I}  F.

Событие, состоящее в том, что значение случайной величины  попадает в промежуток I, обозначается (I). Так же обозначается множество исходов, благоприятных этому событию, так что имеем

(I)  {uU | (u)I}.

Для конкретных промежутков применяются специальные обозначения, именно:

если I  [a; b], то событие (I) обозначается также (a m  m b); если, в частности, a  b, то отрезок [a; b] состоит из одной точки a; событие, состоящее в том, что  принимает это значение, обозначают в виде (  a);

если I  (a; b), то вместо (I) пишут (a <  < b);

если I  [a; b), то вместо (I) пишут (a m  < b);

если I  (–; b), то вместо (I) пишут ( < b);

если I  [a; ), то вместо (I) пишут ( l a).

Для промежутков прочих типов обозначения аналогичны.

Определение 2. Случайные величины  и  называются независимыми, если для любых числовых промежутков I и J события (I) и (J) независимы.

Можно доказать (см., например, [4]), что сумма, разность и произведение двух случайных величин на одном и том же вероятностном пространстве являются случайными величинами на том же пространстве. То же верно и для частного при условии, что делитель не обращается в нуль.

2. Дискретные случайные величины. Случайную величину , принимающую конечное или счетное множество значений, называют дискретной. В этом случае говорят также, что случайная величина имеет дискретное распределение. Вероятность P(  x), рассматриваемая как функция от x, называется законом распределения дискретной случайной величины .

Закон распределения обычно задают таблицей из двух строк: в первой строке перечисляют значения случайной величины, во второй – вероятности этих значений.

x	x1	x2	x3	. . .
P(  x)	p1	p2	p3	. . .

Если x₁, x₂, x₃, … – все значения случайной величины, то сумма событий (  x_j) достоверна и по свойству полной аддитивности имеем

p₁ + p₂ + p₃ + …  1. (1)

Математическое ожидание M дискретной случайной величины  определяется равенством

M  x₁p₁ + x₂p₂ + x₃p₃ + … . (2)

Если число значений случайной величины конечно, то в правой части этого равенства стоит конечная сумма. Если число различных значений  счетно, то правая часть представляет собой числовой ряд. В этом случае, поскольку сумма ряда (2) не должна зависеть от способа нумерации значений , необходимо потребовать, чтобы ряд сходился абсолютно. Если же ряд (2) расходится или сходится условно, то считается, что случайная величина  не имеет математического ожидания.

Число D  M( – M)² называется дисперсией случайной величины . Дисперсия случайной величины характеризует степень разброса ее значений.

Свойства математического ожидания и дисперсии предполагаются известными из курса теории вероятностей (см., например, [8]).

Число называется квадратичным отклонением случайной величины .

Дискретные случайные величины  и  независимы тогда и только тогда, когда при любых x, y независимы события (  x) и (  y).

Рассмотрим основные примеры дискретных распределений.

Биномиальное распределение. Случайная величина  называется распределенной по биномиальному закону (или по закону Бернулли), если она принимает целые значения 0, 1, 2, …, n, причем вероятности появления этих значений определяются равенством

Для такой случайной величины M  np, D  npq.

По биномиальному закону распределено число появлений события в последовательности независимых испытаний (теорема Бернулли).

Распределение Пуассона. Случайная величина  называется распределенной по закону Пуассона, если она принимает все целые неотрицательные значения 0, 1, 2, 3, …, причем вероятности появления этих значений определяются равенством

Для этого распределения имеем M  D  а.

По закону Пуассона распределено число появлений события в последовательности независимых испытаний при условии, что число испытаний весьма велико, а вероятность появления данного события в каждом испытании мала.

Геометрическое распределение. Случайная величина  называется распределенной по геометрическому закону, если она принимает все целые положительные значения 1, 2, 3, …, причем вероятности появления этих значений образуют геометрическую прогрессию, так что имеем

Математическое ожидание и дисперсия случайной величины , распределенной по геометрическому закону, вычисляются по формулам M  , D  .

По геометрическому закону распределено число испытаний до первого успеха. Например, пусть ведется стрельба из орудия до первого попадания в цель и вероятность попадания при каждом выстреле равна p. Вероятность того, что будет сделано n выстрелов, равна, как легко подсчитать, pq^n–1, где q  1 – p.

3. Функция распределения. Непрерывные случайные величины. Если случайная величина имеет более чем счетное множество значений, то вероятность P(  x) появления данного значения x почти для всех значений или даже для всех значений оказывается равной нулю. Следовательно, для такой случайной величины не имеет смысла рассматривать закон распределения. В общем случае для характеристики случайной величины  используется функция распределения, которая определяется на числовой прямой равенством

F(x)  P( < x).

Очевидно, функция распределения является неубывающей на всей числовой прямой. Имеют место следующие свойства (доказательства, см., например, в [4] или в [8]):

(а) F непрерывна слева в любой точке x₀, т. е. выполняется равенство ;

(б) ;

(в) .

Из (а) и (б) вытекает

(г) функция распределения случайной величины  непрерывна в точке x₀ в том и только в том случае, когда P(  x₀)  0.

Случайная величина  называется непрерывной, если ее функция распределения может быть представлена в виде , где f – неотрицательная функция, определенная на всей числовой прямой. Эту функцию называют плотностью вероятностей случайной величины  ^.

Из свойств интеграла с верхним переменным пределом следует, что функция распределения непрерывной случайной величины всюду непрерывна и имеет производную в каждой точке х, где непрерывна плотность вероятностей f, при этом Отсюда ввиду свойства (г) получаем, что P(  x₀)  0 для любой точки x₀.

Как показывает равенство (1), последнее утверждение заведомо не выполняется для дискретных случайных величин, поэтому никакая из них не является непрерывной.

В курсе теории вероятностей (см., например, [4] или [8]) доказывается следующее утверждение: если  – непрерывная случайная величина с плотностью вероятностей f и I – промежуток числовой прямой с концами a и b (случаи a  – или b   не исключаются), то имеет место равенство

. (3)

В частности, поскольку событие () достоверно, имеем .

Математическое ожидание M непрерывной случайной величины  определяется равенством

.

Интеграл в правой части либо абсолютно сходится, либо расходится. В последнем случае говорят, что случайная величина  не имеет математического ожидания.

Дисперсия D и квадратичное отклонение непрерывной случайной величины определяются таким же образом, как и для дискретной.

4. Нормальное распределение. Случайная величина  называется распределенной по нормальному закону (или по закону Гаусса), если она имеет плотность вероятностей

, где и  > 0. (4)

В частности, при a  0 и   1 f (x)  (x). Это распределение является предельным для биномиального распределения, когда число испытаний неограниченно растет.

Функция распределения случайной величины, распределенной по нормальному закону, имеет вид

, где .

Функции  и  используются при решении многих задач статистики. Таблицы значений этих функций приведены в конце данного пособия (табл. 1 и 2).

На рис. 3 и 4 изображены графики плотности вероятностей и функции распределения нормально распределенной случайной величины при разных значениях параметра .

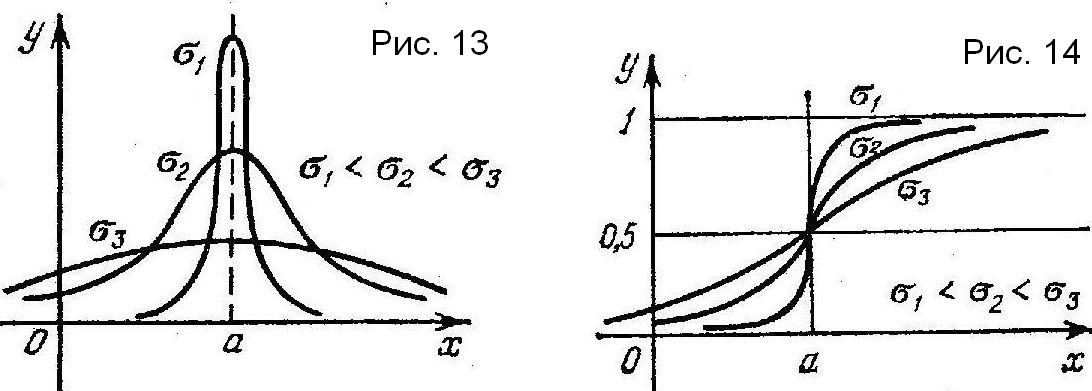
Д

Рис. 3

ля слу

Рис. 4

чайной величины , распределенной по нормальному закону, плотность вероятностей которой определяется равенством (4), имеем M  a, D  ². Вероятность попа дания ее значения в промежуток I с концами b и c вычисляется по формуле, которая следует из (3):

. (5)

Если, в частности, I  (a – 3; a  3), то по формуле (5) получаем     2(3)   (мы воспользовались таблицей значений функции . Найденная вероятность близка к единице, поэтому считается практически достоверным, что в результате проведения эксперимента значение нормально распределенной случайной величины  окажется в интервале (a – 3; a  3) (правило «трех сигм»).

Легко убедиться, что если случайная величина  распределена по нормальному закону, то и случайная величина ab (ab, a  0) распределена по нормальному закону. Можно доказать также, что если случайные величины  и  независимы и распределены по нормальному закону, то и сумма  +  распределена по нормальному закону.

Нормальное распределение играет в статистике особую роль. Оказывается, что при некоторых довольно общих условиях распределение среднего арифметического произвольных случайных величин ₁, ₂, …, _n является практически нормальным, если n достаточно велико. Это устанавливается так называемой центральной предельной теоремой (ее точную формулировку можно найти в [4]).

5. Моменты, асимметрия, эксцесс. При рассмотрении многих задач статистики понятий математического ожидания и дисперсии оказывается недостаточно. В этих случаях используются более общие характеристики случайных величин – моменты и центральные моменты различных порядков. Пусть k.

Моментом k-го порядка случайной величины  называют число _k  M^k.

Центральным моментом k-го порядка случайной величины  называют число _k  M(– M^k.

В частности, имеем M  ₁ и D  ₂.

Если  – дискретная случайная величина, принимающая значения x₁, x₂, x₃, … с вероятностями p_k  P(  x_k), то, очевидно,

,

(если случайная величина имеет счетное множество значений, то моменты существуют тогда и только тогда, когда ряды в правых частях абсолютно сходятся).

Для непрерывной случайной величины с плотностью вероятностей f доказываются равенства:

, (6)

(при условии, что несобственные интегралы в правых частях сходятся, в этом случае они и абсолютно сходятся).

Используя свойства математического ожидания, можно выразить центральные моменты через моменты. Для первых четырех центральных моментов получаем:

₁  M(– M  M– M  0,

₂  M(– M²  M(²– 2M  (M)²)  M²– 2(M)²  + (M)²)  M²– (M)²  ,

₃  M(– M³  M(³ – 3²M + 3(M)² – (M)³)   M³ – 3M²M + 3(M)³ – (M)³  M³ – 3M²M + 2(M)³   ,

_k  M(– M^k  M(⁴ – 4³M + 6²(M)² – 4(M)³ + + (M)⁴)  M⁴ – 4M³M + 6M²(M)² – 4(M)⁴ + (M)⁴    .

Эти первые моменты играют важную роль в статистике.

Если график плотности вероятностей симметричен относительно прямой x  M, то, как легко убедиться, цент­ральные моменты нечетного порядка все равны нулю.

Действительно, используя в этом случае замену переменной y  x – M во втором из интегралов (6), получаем . Так как (– y)^k  – y^k и f (M – y)   f (M  y), то под знаком интеграла стоит нечетная функция, а интеграл от нечетной функции по промежутку, симметричному относительно точки 0, равен нулю.

Например, таким свойством обладает нормальное распределение (см. график плотности вероятностей на рис. 3). Для несимметричных распределений центральные моменты нечетных порядков, за исключением первого, отличны от нуля, поэтому их можно использовать как характеристику отклонения от симметричности. Наиболее удобной характеристикой оказывается число

A  ,

где – квадратичное отклонение. Величину A называют коэффициентом асимметрии или просто асимметрией распределения случайной величины .

Если A > 0, то часть графика плотности вероятностей f, лежащая справа от точки M, оказывается более пологой, чем часть, лежащая слева от точки M (рис. 5а); если же A < 0, то часть графика плотности f, лежащая справа от точки M, оказывается, напротив, более крутой, чем часть, лежащая слева от точки M (рис. 5б) ¹.

Для характеристики отклонения распределения случайной величины  от нормального используется величина

E  ,

называемая эксцессом распределения.

Е сли  распределена по нормальному закону, то, как легко подсчитать, ₄ /⁴  3, значит, E  0. Если E > 0, то график плотности вероятностей имеет бóльшую крутизну, чем для нормального распределения; при E < 0 график более пологий сравнительно с нормальным распределением (рис. 6).

6. Ковариация. Корреляция. Ковариационная матрица. Ковариацией случайных величин¹  и  называется число

cov (, ) = M(( – M)( – M)).

Ясно, что cov (, ) = D. Имеем также cov (, ) =  M( – M – M  MM) = M() – MM.

Пусть D> 0, D > 0 ². Число

называется коэффициентом корреляции случайных величин  и . Случайные величины  и  называются некоррелированными, если .

Если  и  независимы, то M() = MM, значит, . Таким образом, независимые случайные величины некоррелированы. Обратное утверждение, вообще говоря, неверно, как показывает следующий

Пример. Пусть  – любая случайная величина, принимающая все действительные значения и имеющая четную плотность вероятностей f, и пусть  = ². Очевидно, что случайные величины  и  зависимы, однако имеем M = , M() = M³ = (т. к. под знаком каждого интеграла нечетная функция), следовательно, .

Для любых случайных величин  и  с положительной дисперсией выполняется неравенство | r(, ) | m 1.

Действительно, имеем M(( – M)  x( – M))² =

= M(( – M)²  2x( – M)( – M)  x²( – M)²) =

 D2x cov(x²D

Как видно из исходного выражения, полученный квадратный трехчлен не принимает отрицательных значений и, следовательно, не имеет двух различных действительных корней. Поэтому его дискриминант не положителен, так что (cov ())² – D D m 0, откуда |cov ()| m , а значит, m 1.

Коэффициент корреляции характеризует степень зависимости случайных величин. Если он равен 0, то случайные величины почти независимы или совсем независимы; чем ближе его модуль к единице, тем больше зависимость. Можно доказать, что при = 1 любая из этих случайных величин линейно выражается через другую, например,  = a + b, где a, bÎÑ и a ¹ 0.

Ковариационной матрицей последовательности случайных величин ₁, ₂, ..., _n называется матрица

,

или, коротко, S = (cov (_i, _j)).

Для любых действительных чисел a₁, a₂, ..., a_n, b₁, b₂, ..., b_n имеет место равенство

,

где a = и b = – одностолбцовые матрицы, а верхний индекс T означает переход к транспонированной матрице: a^T  (a₁ a₂ ... a_n).

Действительно,

– .

В частности, получаем l 0, т. е. S – матрица ква­дратичной формы, принимающей лишь неотрицательные значения. Такую матрицу (а также и саму квадратичную форму) называют положительно полуопределенной. Если матрица S не особенная ¹, то квадратичная форма равна 0 только при a₁ = a₂ = ... = a_n = 0 (в этом случае форму называют положительно определенной). Если же ранг матрицы S меньше n, то существует ненулевой вектор а, для которого . Это означает, что является постоянной на некотором множестве вероятности 1 (см. сноску 2 на стр. 30).

7. Случайные векторы. Конечная последовательность действительных чисел

x  (x₁, x₂, …, x_n)

называется n-мерным вектором. Множество всех n-мерных векторов обозначается ⁿ.

Сумма n-мерных векторов x  (x₁, x₂, …, x_n) и y  ( y₁, y₂, …, y_n) и произведение вектора x на число с определяются равенствами:

x + y  (x₁ + y₁, x₂ + y₂ , …, x_n + y_n);

сx  (сx₁, сx₂, …, сx_n).

Полагаем также x – y  x + (–1)y. Легко убедиться, что введенные операции обладают теми же свойствами, что и аналогичные операции над геометрическими векторами, так что множество ⁿ вместе с введенными операциями образует векторное пространство. Совокупность векторов

e₁  (1, 0, ..., 0), e₂  (0, 1, ..., 0), …, e_n  (0, 0, ..., 1)

образует базис пространства ⁿ, т. к. любой вектор x  (x₁, x₂, …, x_n)  ⁿ единственным образом линейно выражается через векторы e₁, e₂, ..., e_n:

x  x₁e₁ + x₂e₂ + … + x_ne_n.

Для любых n-мерных векторов x  (x₁, x₂, …, x_n) и y  (y₁, y₂, …, y_n) полагают

x  y  x₁ y₁ + x₂ y₂ + ... + x_n y_n;

.

Число x  y называют скалярным произведением векторов x и y, а число | x | – модулем вектора x.

Для любых векторов x, y  ⁿ и любого действительного числа с справедливы соотношения:

| сx |  | с |  | x |, | x + y | m | x | + | y |, | x  y | m | x |  | y |.

Рассмотрим теперь функцию f, определенную на произвольном множестве U, значениями которой являются векторы пространства ⁿ. Функцию с такими значениями называют векторной функцией или вектор-функцией.

Пусть uU и f (u)  x  (x₁, x₂, …, x_n). Положим

f₁(u)  x₁, f₂(u)  x₂, …, f_n(u)  x_n.

Эти равенства определяет на множестве U n числовых функций f₁, f₂, …, f_n, которые называют компонентами вектор-функции f. Пишут

f   ( f₁, f₂, …, f_n).

Теперь мы можем сформулировать важное для дальнейшего

Определение. Случайным вектором на вероятностном пространстве (U, F, P) называется всякая вектор-функция ξ  (₁, ₂, …, _n), все компоненты которой являются случайными величинами на том же пространстве.

Случайный вектор с n компонентами называют также n‑мерной случайной величиной.

Из определения, в частности, следует, что для любых чисел x₁, x₂, …, x_n будет (_k < x_k)F, следовательно, можно рассматривать событие (₁ < x₁)(₂ < x₂)...(_n < x_n). Функция от n переменных

F(x₁, x₂, ..., x_n)  P((₁ < x₁)(₂ < x₂)...(_n < x_n)) (7)

называется функцией распределения случайного вектора ξ.

Если ₁, ₂, …, _n независимы, то F(x₁, x₂, ..., x_n)   P(₁ < x₁)P(₂ < x₂)...P(_n < x_n)  F₁(x₁)F₂(x₂)...F_n(x_n), где F_j – функция распределения для _j ( j  1, 2, ..., n).

Если существует неотрицательная функция f от n переменных такая, что для любых чисел x₁, x₂, …, x_n выполняется равенство

, (8)

то случайный вектор ξ называется непрерывным, а функция f – ее плотностью вероятностей.

Любая компонента непрерывного случайного вектора – непрерывная случайная величина. Например, для функции распределения первой компоненты из (7) и (8) следует

так что ₁ имеет плотность вероятностей

.

Математическое ожидание и дисперсия случайного вектора ξ  (₁, ₂, …, _n) определяются равенствами:

Mξ  (M₁, M₂, ..., M_n); Dξ  (cov (_i, _j)).

Таким образом, Mξ представляет собой n-мерный вектор, а Dξ – симметричную положительно полуопределенную квадратную матрицу порядка n, являющуюся ковариационной матрицей компонент случайного вектора.

Рассмотрим, в частности, двумерный случайный вектор (, ), имеющий плотность вероятностей f. Его компоненты  и  имеют плотности вероятностей соответственно и .

Отношение называют условной плотностью вероятностей случайной величины  при условии, что случайная величина  принимает значение y.

Отношение называют условной плотностью вероятностей случайной величины  при условии, что случайная величина  принимает значение x.

Используются обозначения:

.

Введенные условные плотности вероятностей обладают обычными свойствами плотности. Например, получаем .

Обозначают также

, .

Первую величину называют условным математическим ожиданием случайной величины  при условии (  y), вторую – условным математическим ожиданием случайной величины  при условии (  x).

Условные математические ожидания определяются и для случая, когда одна или обе случайные величины  и  дискретны. Например, если  принимает счетное множество значений x₁, x₂, x₃, ... и P(  y)  0, полагают

,

если ряд в правой части сходится абсолютно.