
- •С. Б. Волкова математическая статистика и планирование эксперимента
- •§ 2. Интервальные оценки . . . . . . . . . . . . . . . . . . . . . . . . . 50
- •§ 3. Проверка статистических гипотез . . . . . . . . . . . . . . . . 58
- •§ 2. Доверительные интервалы для параметров
- •§ 3. Полные факторные эксперименты типа 2k.
- •§ 4. Оптимизация планов. Поиск экстремума
- •Предисловие
- •Введение
- •§ 1. Математическая модель статистического эксперимента
- •§ 2. Случайные величины
- •Глава 1. Элементы математической статистики
- •§ 1. Выборочный метод. Точечные оценки
- •§ 2. Интервальные оценки
- •§ 3. Проверка статистических гипотез
- •2. Проверка гипотезы о равенстве дисперсий двух нормально распределенных случайных величин.
- •§ 4. Однофакторный дисперсионный анализ
- •§ 5. Элементы теории корреляции
- •Глава 2. Планирование эксперимента
- •§ 1. Пассивный эксперимент
- •7. Оценивание функции отклика и ее параметров.
- •§ 2. Доверительные интервалы для параметров функции отклика и гипотеза адекватности
- •§ 3. Полные факторные эксперименты типа 2k . Анализ факторных экспериментов
- •4. Насыщенное и ненасыщенное планирование.
- •§ 4. Оптимизация планов. Поиск экстремума функции отклика
- •Для распределения 2 с n степенями свободы
- •Критические точки критерия 2:
- •Критические точки критерия 2:
- •Литература для дополнительного чтения
- •Светлана Борисовна Волкова математическая статистика и планирование эксперимента
- •162600, Г. Череповец, пр. Луначарского, 5.
§ 3. Полные факторные эксперименты типа 2k . Анализ факторных экспериментов
1. Полные факторные эксперименты и кодированные переменные. При проведении экспериментальных исследований часто применяются факторные эксперименты.
Пусть
![]() – функция отклика и задан план, матрица
которого есть
– функция отклика и задан план, матрица
которого есть
![]() (i
1, 2, ..., k; u
1, 2,
..., N), где
(i
1, 2, ..., k; u
1, 2,
..., N), где
![]() – значение переменной (фактора)
– значение переменной (фактора)
![]() в u‑м опыте. Каждое
из различных значений, принимаемых
переменной
в эксперименте, называют уровнем
этой переменной. Обозначим через si
число различных уровней фактора Xi.
в u‑м опыте. Каждое
из различных значений, принимаемых
переменной
в эксперименте, называют уровнем
этой переменной. Обозначим через si
число различных уровней фактора Xi.
Определение 1. Эксперимент, в котором уровни каждого фактора комбинируются со всеми уровнями других факторов, называется полным факторным экспериментом.
Полный факторный
эксперимент состоит из
![]() различных экспериментов, поэтому его
называют экспериментом типа
различных экспериментов, поэтому его
называют экспериментом типа
![]() .
.
Определение
2. План называется симметричным,
если все факторы имеют одинаковое число
уровней, т. е.
![]() В этом случае полный факторный эксперимент
принято называть экспериментом типа
sk,
где k –
число факторов.
В этом случае полный факторный эксперимент
принято называть экспериментом типа
sk,
где k –
число факторов.
Предположим, что
число различных значений, которые может
принимать переменная
![]() ,
в каждом опыте равно 2, т. е. s
2. Тогда говорят,
что переменная
в каждом опыте варьируется на двух
уровнях. Обозначим эти уровни через
,
в каждом опыте равно 2, т. е. s
2. Тогда говорят,
что переменная
в каждом опыте варьируется на двух
уровнях. Обозначим эти уровни через
![]() и
и
![]() .
Если
.
Если
![]() ,
то
,
то
![]() называют верхним уровнем, а
– нижним уровнем фактора
.
называют верхним уровнем, а
– нижним уровнем фактора
.
Обозначим
![]() ,
,
![]() и введем новые переменные
и введем новые переменные
![]() (i
1, 2,
..., k).
(i
1, 2,
..., k).
Переменные xi
называют кодированными переменными.
Легко проверить, что они могут принимать
лишь два значения 1 (верхний уровень) и
–1 (нижний уровень). Заменяя переменные
кодированными переменными
![]() ,
можно представить функцию отклика в
виде
,
можно представить функцию отклика в
виде
![]() .
(1)
.
(1)
2. Полные факторные
эксперименты типа 22 и 23.
Если число независимых переменных равно
двум, то равенство (1) приводится к виду
![]() .
Результаты наблюдений, отвечающих
всевозможным комбинациям уровней
переменных x1
и x2, сводятся
в таблицу.
.
Результаты наблюдений, отвечающих
всевозможным комбинациям уровней
переменных x1
и x2, сводятся
в таблицу.
Номер опыта |
|
|
|
Наблюдения |
1 |
– 1 |
– 1 |
1 |
y1 |
2 |
1 |
– 1 |
– 1 |
y2 |
3 |
– 1 |
1 |
– 1 |
y3 |
4 |
1 |
1 |
1 |
y4 |
Пусть функция отклика имеет вид
![]()
и в каждом варианте испытаний проводится по одному наблюдению. Тогда имеем полный факторный эксперимент типа 22. Матрица плана и матрица планирования:
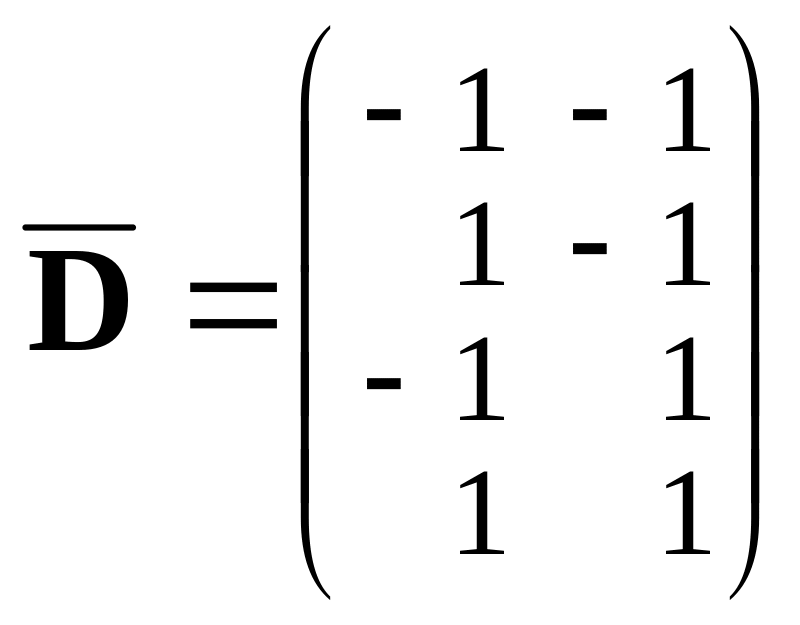 ,
,
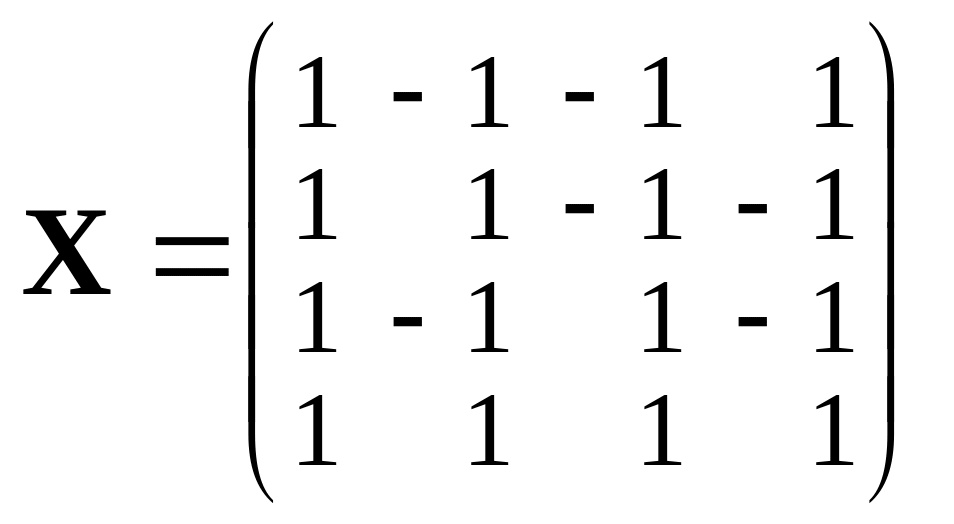 .
.
Столбцы матрицы X попарно ортогональны, следовательно, планирование является ортогональным. Отсюда, используя результаты п. 7 § 1, получаем, что МНК‑оценки параметров некоррелированны и имеют вид
![]() ,
,
где Xj –
j-й столбец матрицы
Х, при этом
![]() .
.
Пусть теперь число переменных равно трем и функция отклика имеет вид
![]() .
.
Рассмотрим все
возможные комбинации уровней кодированных
переменных
,
и
![]() .
.
Номер опыта |
|
|
|
|
|
|
|
Наблю- дения |
1 |
– 1 |
– 1 |
– 1 |
1 |
1 |
1 |
– 1 |
y1 |
2 |
1 |
– 1 |
– 1 |
– 1 |
– 1 |
1 |
1 |
y2 |
3 |
– 1 |
1 |
– 1 |
– 1 |
1 |
– 1 |
1 |
y3 |
4 |
1 |
1 |
– 1 |
1 |
– 1 |
– 1 |
– 1 |
y4 |
5 |
– 1 |
– 1 |
1 |
1 |
– 1 |
– 1 |
1 |
y5 |
6 |
1 |
– 1 |
1 |
– 1 |
1 |
– 1 |
– 1 |
y6 |
7 |
– 1 |
1 |
1 |
– 1 |
– 1 |
1 |
– 1 |
y7 |
8 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
y8 |
Здесь, как легко убедиться, планирование является ортогональным. Поэтому МНК-оценки параметров j некоррелированны и имеют вид
![]() ,
,
при этом
![]() .
.
Пример 1. Полный двухфакторный эксперимент проводится на двух уровнях.
Переменные |
X1 |
X2 |
Нижний уровень |
64 |
45 |
Верхний уровень |
74 |
85 |
Получены результаты
исследований:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Для нахождения
МНК-оценок
![]() параметров
параметров
![]() ортогонального плана пользуются
расчетной таблицей.
ортогонального плана пользуются
расчетной таблицей.
i |
|
|
|
|
|
|
|
1 |
– 1 |
– 1 |
1 |
66 |
– 66 |
– 66 |
66 |
2 |
1 |
– 1 |
– 1 |
68 |
68 |
– 68 |
– 68 |
3 |
– 1 |
1 |
– 1 |
48 |
– 48 |
48 |
– 48 |
4 |
1 |
1 |
1 |
45 |
45 |
45 |
45 |
С помощью расчетной таблицы получаем требуемые оценки:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Значит, оценка функции отклика есть
![]() .
(2)
.
(2)
Возвращаясь к исходным переменным, имеем:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
значит,
,
значит,
![]() ,
,
![]() .
Подставляя найденные выражения в (2),
получаем
.
Подставляя найденные выражения в (2),
получаем
![]()
![]() .
.
Пример 2. Полный трехфакторный эксперимент проводится на двух уровнях.
Переменные |
X1 |
X2 |
X3 |
Нижний уровень |
12 |
17 |
26 |
Верхний уровень |
15 |
25 |
30 |
Результаты
исследований:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Составим расчетную
таблицу для нахождения МНК‑оценок
параметров
![]() ортогонального плана.
ортогонального плана.
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
x1 |
–1 |
1 |
–1 |
1 |
–1 |
1 |
–1 |
1 |
x2 |
–1 |
–1 |
1 |
1 |
–1 |
–1 |
1 |
1 |
x3 |
–1 |
–1 |
–1 |
–1 |
1 |
1 |
1 |
1 |
x1x2 |
1 |
–1 |
–1 |
1 |
1 |
–1 |
–1 |
1 |
x1x3 |
1 |
–1 |
1 |
–1 |
–1 |
1 |
–1 |
1 |
x2x3 |
1 |
1 |
–1 |
–1 |
–1 |
–1 |
1 |
1 |
x1x2x3 |
–1 |
1 |
1 |
–1 |
1 |
–1 |
–1 |
1 |
yi |
5,6 |
7,7 |
8,1 |
9,6 |
8,6 |
5,1 |
6,4 |
6,9 |
x1yi |
–5,6 |
7,7 |
–8,1 |
9,6 |
–8,6 |
5,1 |
–6,4 |
6,9 |
x2yi |
–5,6 |
–7,7 |
8,1 |
9,6 |
–8,6 |
–5,1 |
6,4 |
6,9 |
x3yi |
–5,6 |
–7,7 |
–8,1 |
–9,6 |
8,6 |
5,1 |
6,4 |
6,9 |
x1x2yi |
5,6 |
–7,7 |
–8,1 |
9,6 |
8,6 |
–5,1 |
–6,4 |
6,9 |
x1x3yi |
5,6 |
–7,7 |
8,1 |
–9,6 |
–8,6 |
5,1 |
–6,4 |
6,9 |
x2x3yi |
5,6 |
7,7 |
–8,1 |
–9,6 |
–8,6 |
–5,1 |
6,4 |
6,9 |
x1x2x3yi |
–5,6 |
7,7 |
8,1 |
–9,6 |
8,6 |
–5,1 |
–6,4 |
6,9 |
Используя расчетную
таблицу, так же, как и в предыдущем
примере, получаем требуемые оценки
параметров:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
Следовательно,
.
Следовательно,
![]()
![]() .
(3)
.
(3)
Возвращаемся к исходным переменным.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
значит,
,
значит,
![]() ,
,
![]() ,
,
![]() .
Подставляя эти выражения в (3), получаем
окончательно
.
Подставляя эти выражения в (3), получаем
окончательно
![]()
3. Факторные
эксперименты с повторными наблюдениями.
Пусть
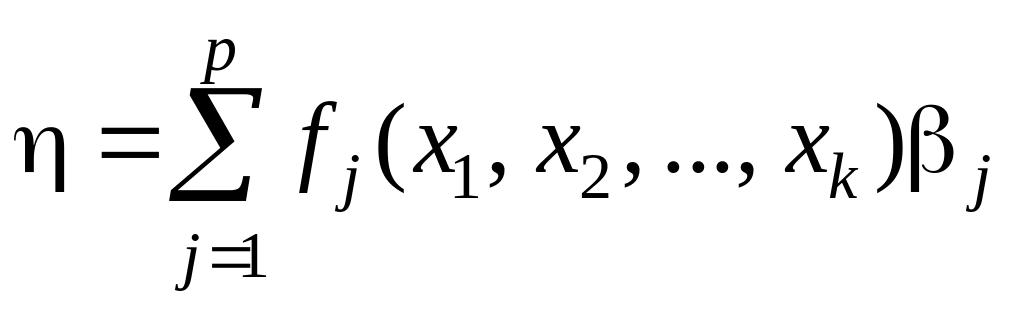 – функция отклика,
;
m, m,
..., m – спектр плана
(число наблюдений в каждой точке xl
одно и то же и равно m),
mn
N. Пусть xl
(x1l,
x2l,
..., xkl)
и
– функция отклика,
;
m, m,
..., m – спектр плана
(число наблюдений в каждой точке xl
одно и то же и равно m),
mn
N. Пусть xl
(x1l,
x2l,
..., xkl)
и
![]() – повторные наблюдения в точке xl
– повторные наблюдения в точке xl
![]() .
.
Матрицу плана
![]() можно представить в виде матрицы из m
блоков следующим образом:
можно представить в виде матрицы из m
блоков следующим образом:
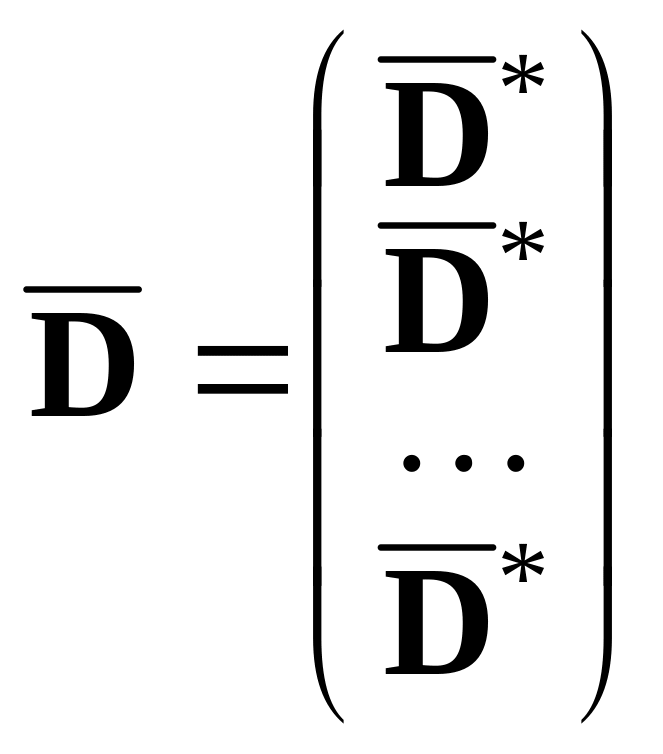 ,
где
,
где
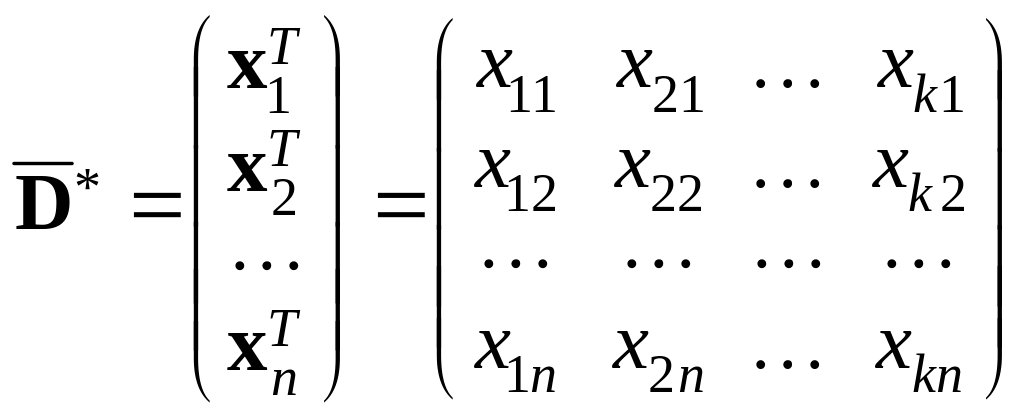 .
.
Таким образом,
![]() – матрица размеров
– матрица размеров
![]() с различными строками,
– матрица размеров
с различными строками,
– матрица размеров
![]() .
.
Определение.
План называется полным факторным
планом типа 2k
с повторными наблюдениями кратности
m, если матрица
![]() является матрицей полного факторного
плана типа 2k.
является матрицей полного факторного
плана типа 2k.
Пример.
Пусть
![]() – функция отклика и задан план:
– функция отклика и задан план:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
причем в каждой точке число наблюдений
m
2. Тогда матрица плана записывается в
виде:
,
причем в каждой точке число наблюдений
m
2. Тогда матрица плана записывается в
виде:
![]() ,
где
,
где
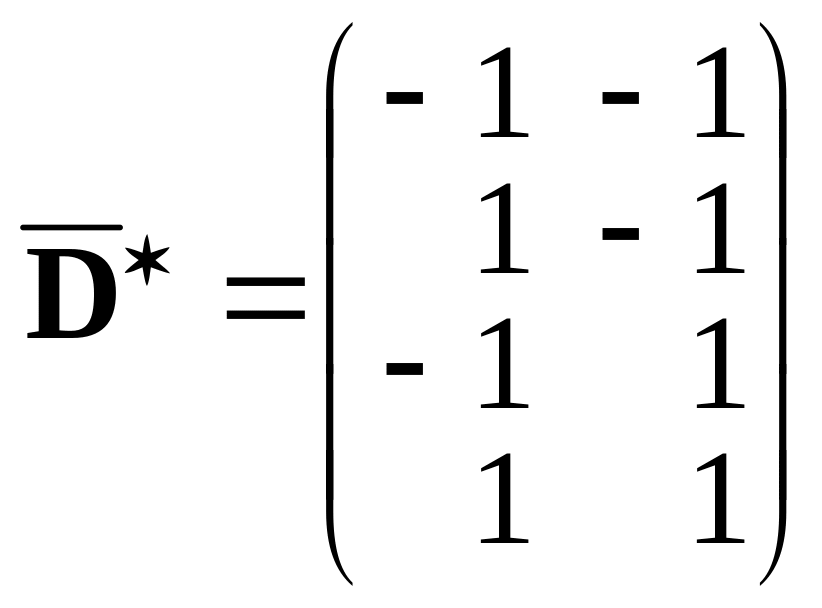 .
.
Так как
![]() – матрица плана полного факторного
эксперимента типа 22, то данный
план является полным факторным планом
с повторными наблюдениями кратности
2.
– матрица плана полного факторного
эксперимента типа 22, то данный
план является полным факторным планом
с повторными наблюдениями кратности
2.
Матрица планирования имеет вид
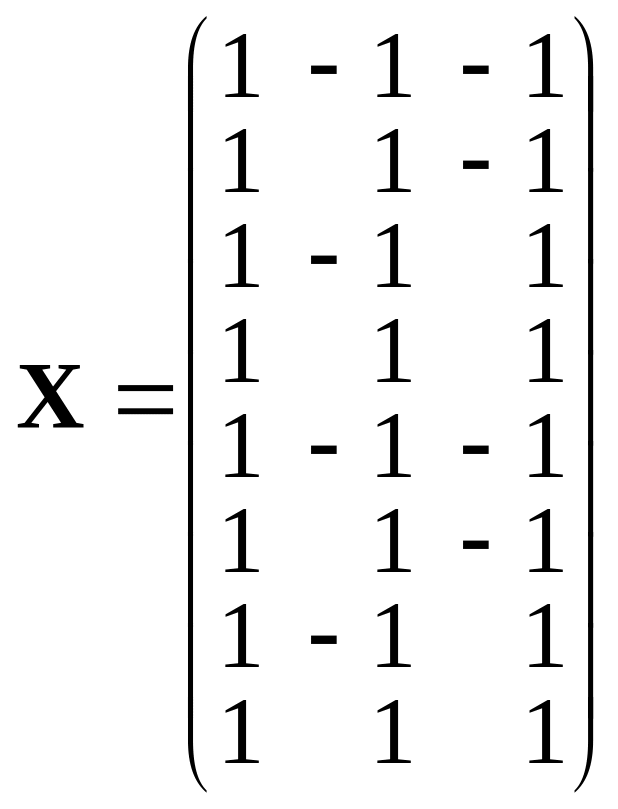
и является матрицей ортогонального планирования.
Если
![]() – матрица планирования, соответствующая
функции отклика
– матрица планирования, соответствующая
функции отклика
![]() и матрице плана
,
то из ортогональности планирования
для МНК-оценки вектора β имеем
равенство
и матрице плана
,
то из ортогональности планирования
для МНК-оценки вектора β имеем
равенство
![]() ,
в котором
,
в котором
![]() ,
,
![]() ,
а значит,
,
а значит,
![]() ( j
0, 1, ..., p). В этом случае
оценки
( j
0, 1, ..., p). В этом случае
оценки
![]() некоррелированны и имеют дисперсию
некоррелированны и имеют дисперсию
![]() .
.
