4. Насыщенное и ненасыщенное планирование.

Определение 1. Пусть матрица планирования X имеет ранг, равный числу p неизвестных параметров в функции отклика. Факторный план называется насыщенным, если p  N, и ненасыщенным, если p < N.

Ненасыщенность плана полного факторного эксперимента означает, что имеется избыточность опытов, необходимых для нахождения МНК-оценок параметров в функции .

Пример 1. Пусть и планируется полный факторный эксперимент типа 2². Тогда планирование будет насыщенным, т. к. ранг матрицы планирования X равен 4 и при этом число наблюдений N и число неизвестных параметров p  также равны 4.

Пример 2. Если и имеется полный факторный эксперимент типа 2², то планирование будет ненасыщенным, т. к. ранг матрицы планирования

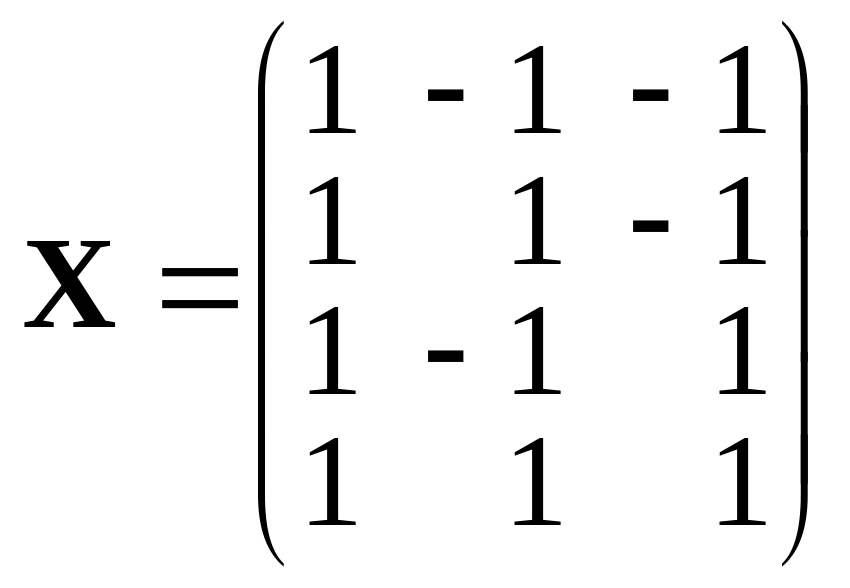
равен 3, а .

Определение 2. Пусть n – число точек спектра факторного плана с повторными наблюдениями кратности m (N  mn) и r – ранг матрицы планирования X. Тогда план называется насыщенным, если , и ненасыщенным, если .

5. Проверка гипотезы адекватности. Рассмотрим факторный эксперимент с кратными повторными наблюдениями y_ls (l  1, 2, ..., n; s  1, 2, ..., m). Проверим гипотезу H₀ адекватности модели

, (4)

где – известные функции, задаваемые равенствами вида (1 m i₁ < i₂ < ... < i_q m k), а – неизвестные параметры. Функции отклика (4) и матрице (i  1, 2, ..., k; u  1, 2, ..., N; N  mn) полного факторного плана соответствует матрица планирования ( j  1, 2, ..., p₀; u  1, 2, ..., N). Столбцы матрицы X⁰ должны удовлетворять условиям:

( j = 2, 3, …, p); (5)

( j = 1, 2, …, p); (6)

. (7)

Будем предполагать, что наблюдения y_ls являются нормальными и некоррелированными, причем , где – вектор-столбец наблюдений; – неизвестный параметр.

Гипотеза состоит в том, что My  X⁰β⁰, где . Эта гипотеза проверяется при альтернативной гипотезе : My  X⁰β⁰.

Для проверки гипотезы нужно вычислить отношение . Величина представляет собой несмещенную оценку для . Полагая в формуле (6) § 2 m₁  m₂  ...  m_i  m, получаем

.

Таким образом,

. (8)

Оценка (5) § 2 дисперсии , связанная с неадекватностью модели, есть , где r – ранг матрицы X⁰.

Пусть r  , тогда, учитывая (5) – (7), получаем

, (9)

где , j = 1, 2, ..., p₀.

Далее вычисляем и по таблице распределения Фишера по уровню значимости a и степеням свободы n – r и N – n находим .

Если , то гипотеза H₀ принимается.

Если , то гипотеза H₀ отклоняется.

Пример. Предположим, что зависимость прочности бетона R от двух факторов – расхода цемента X₁ и расхода воды X₂ – имеет вид: . Полный двухфакторный эксперимент проводится на двух уровнях:

Уровень	Расход цемента X1	Расход воды X2
Нижний	270	155
Верхний	370	185

Результаты исследований представлены таблицей.

i
1	28,6	31,1	29,5	29,7
2	44,3	47,8	46,2	46,1
3	22,9	24,6	21,9	23,1
4	38,7	38,7	35,3	36,7

МНК-оценки параметров ортогонального планирования находятся так же, как в примере 1 п. 3: ; ; , отсюда оценка функции отклика – , или, переходя к исходным переменным, .

Проверим, является ли полученная модель адекватной. Имеем N  12, n  4, m  3, r  3. По формулам (8) и (9)

,

.

Следовательно, . Далее по таблице критических точек распределения Фишера по уровню значимости a  0,05 и степеням свободы n – r  1 и N – n  8 находим . Так как , то гипотеза, утверждающая, что модель адекватна, принимается.