7. Оценивание функции отклика и ее параметров.

Пусть – одномерная функция отклика. Ее оценка в любой точке имеет вид:

. (15)

Если – МНК-оценка вектор-столбца неизвестных параметров β  (₁ ₂ ... _p)^T, полученная по наблюдениям в точках x₁, x₂, ..., x_N, и ранг матрицы планирования X равен p, то оценка (15) является несмещенной и при заданной матрице плана (12) в классе линейных несмещенных оценок имеет минимальную дисперсию.

Пример 1. Пусть ; тогда оценка будет иметь вид .

Если столбцы матрицы планирования попарно ортогональны, т. е. при i  j (i, j  1, 2, ..., p) выполняются равенства

f_i(x₁) f_j(x₁)  f_i(x₂) f_j(x₂)  ...  f_i(x_N) f_j(x_N)  (16)

то говорят, что имеет место ортогональное планирование.

Обозначим X_j  ( f_j(x₁), f_j(x₂), ..., f_j(x_N)), тогда имеем

f_i(x₁)²  f_i(x₂)²  ...  f_i(x_N)²  | X_j |² . (17)

Заметим, что вектор X_j, рассматриваемый как вектор‑столбец, совпадает с j-м столбцом матрицы X, поэтому из (16) и (17) следует

,

откуда 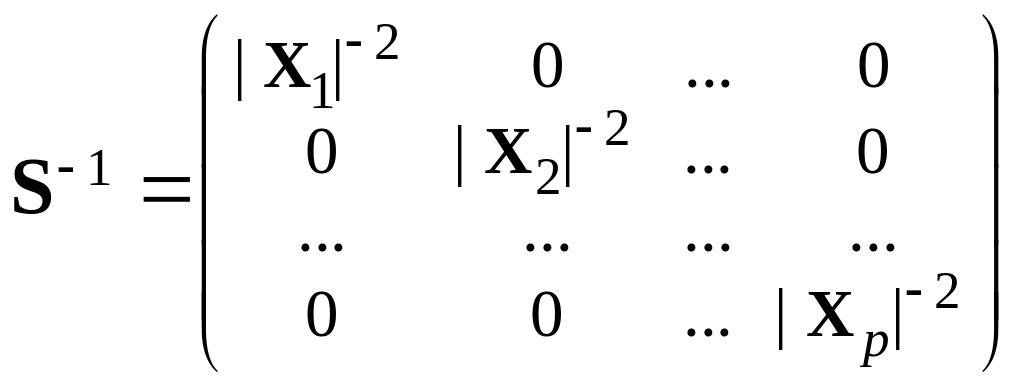и по формуле (9)

.

Отсюда при всех j  1, 2, ..., p следует

. (18)

Равенство (10) показывает, что МНК-оценки (18) некоррелированы и при этом .

Пример 2. Пусть , 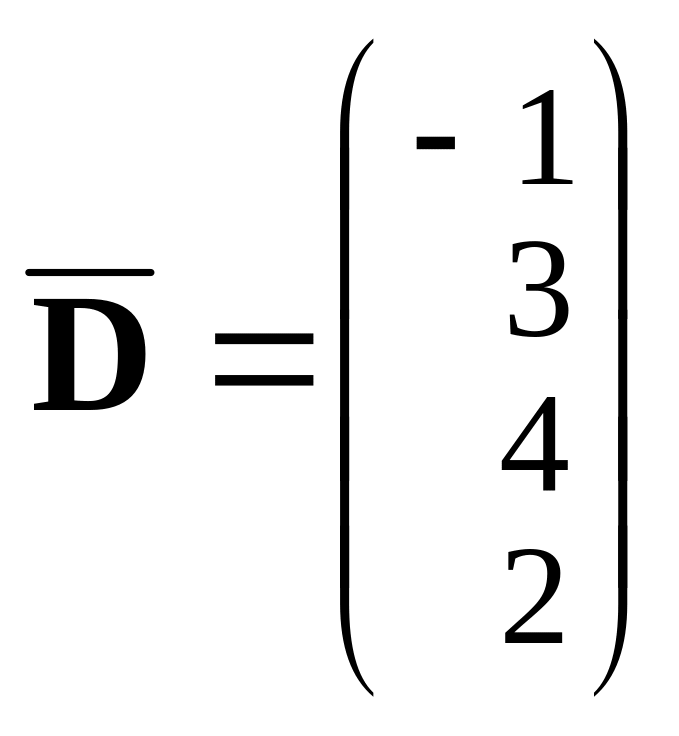и . Тогда f₀(x)  1, f₁(x)  x,

,

причем , так что имеет место ортогональное планирование. Поскольку

|X₁|²  1² + 1² + + 1² + 1²  4,

,

то по формуле (18) получаем

,

.

Если планирование не является ортогональным, но матрицу X можно разбить на подматрицы: X = (X₁ X₂ ... X_l) так, что будет (i < j; i, j  1, 2, ..., l; O – нулевая матрица), то для оценок можно получить формулу, обобщающую формулу (18). Например, пусть имеет место случай l  2, т. е.

,

где . Пусть β = (₁ ₂ ... _p)^T, β₁  (₁ ₂ ... _q)^T и β₂  (_q1 _q2 ... _p)^T, тогда .

В п. 3 было доказано, что МНК-оценка вектора удовлетворяет нормальному уравнению (8), поэтому имеем , или, поскольку ,

.

Отсюда следует , , и, таким образом, получаем формулы

, . (18´)

Пример 3. Пусть заданы , и вектор-столбец наблюдений .

Тогда f_j(x)  x_j ( j  1, 2, 3, 4), следовательно, . Полагая , где , , имеем , , .

По формулам (18´) находим

,

.

8. Оценивание параметров модели при повторных наблюдениях. Пусть задана функция отклика, определенная в области G: . Вве­дем в рассмотрение вектор-функцию f  ( f₁, f₂, ..., f_p) (отождествляемую, как обычно, с одностолбцовой матрицей ( f₁  f₂  ...  f_p)^T ). Тогда функцию отклика можно записать в матричном виде

.

Пусть также задан план, спектр которого m₁, m₂, ..., m_n (m_i – число наблюдений в точке x_i).

Наблюдения в одной точке называют повторными. Матрица плана при наличии повторных наблюдений имеет вид , где каждый блок – матрица размера , имеющая одинаковых строк. Вектор-столбец наблюдений можно записать в виде , где блок соответствует матрице .

Матрица планирования также может быть записана в блочном виде: , где – матрица размера (i  1, 2, ..., n). Отсюда где

,

так что и, следовательно,

. (19)

Определим теперь матрицы

, .

Матрица состоит из строк матрицы , отвечающих различным точкам плана.

Легко убедиться, что . Отсюда и из (19) следует матричное равенство

. (20)

Обозначим (среднее значение повторных наблюдений в точке , i  1, 2, ..., n), тогда получаем

,

где обозначено .

Используя этот результат и формулы (9) и (20), получаем .

Если, в частности, , при всех i  1, 2, ..., n, то и тогда имеем .

Пример. Пусть даны функция отклика и матрица плана

.

Знаком « » указаны наблюдения в соответствующих точках плана. Здесь , а значит, .

Имеем , , , где ; . Следовательно,   .