МІНІСТЕРСТВО ОСВІТИ УКРАЇНИ

НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ УКРАЇНИ

«КИЇВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ»

Кафедра промислової електроніки

МЕТОДИЧНІ ВКАЗІВКИ ДО ВИВЧЕННЯ

КУРСУ «ТЕОРІЯ ЕЛЕКТРОМАГНІТНОГО ПОЛЯ»

РОЗДІЛ «ОСНОВНІ РІВНЯННЯ ЕЛЕКТРОМАГНІТНОГО ПОЛЯ»

МІНІСТЕРСТВО ОСВІТИ УКРАЇНИ

НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ УКРАЇНИ

«КИЇВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ»

Кафедра промислової електроніки

МЕТОДИЧНІ ВКАЗІВКИ ДО ВИВЧЕННЯ

КУРСУ «ТЕОРІЯ ЕЛЕКТРОМАГНІТНОГО ПОЛЯ»

РОЗДІЛ «ОСНОВНІ РІВНЯННЯ ЕЛЕКТРОМАГНІТНОГО ПОЛЯ»

ДЛЯ СТУДЕНТІВ СПЕЦІАЛЬНОСТІ

7.09.08.03 - «Електронні системи»

УСІХ ФОРМ НАВЧАННЯ

Затверджено на засіданні

кафедри промислової електроніки

протокол №1 від 12 січня 2000 р.

Київ НТУУ «КПІ» 2000

Методичні вказівки до вивчення курсу «Теорія електромагнітного поля», розділ «Основні рівняння електромагнітного поля» для студентів спеціальності 7.09.08.03 - «Електронні системи» всіх форм навчання. - К.: НТУУ «КПІ», 2000. - ХХ с.

Навчальне видання

Методичні вказівки до вивчення курсу «Теорія електромагнітного поля»,

розділ «Основні рівняння електромагнітного поля»

Укладач:: Перекрест Валерій Васильович

Відповідальний редактор: Жуйков В.Я.

Рецензенти: І.Є.Коротєєв, проф., докт.техн.наук

В.В.Рогаль, доц.,канд.техн.наук

ВСТУП

Курс «Теорія електромагнітного поля» є одним з основних в системі дисциплін, які забезпечують загальноінженерну підготовку студентів за фахом 7.09.08.03 - «Електронні системи». Дана дисципліна базується на курсах «Математичний аналіз», «Фізика», «Теорія ланцюгів» і є базовою для вивчення наступних курсів: «Електромагнітна техніка», «Енергетична електроніка», «Моделювання в електроніці» та ін.

Дані методичні вказівки є першою частиною курсу «Теорія електромагнітного поля».

Розділ «Лінії з розподіленими параметрами» знайомить студентів з поняттям ліній з розподіленими параметрами, їх властивостями та параметрами.

Основною метою методичних вказівок є допомога студентам у вивченні основних підходів до описання електромагнітних процесів у таких лініях та методів їх розрахунку, виконанні розрахунково-графічної роботи і самостійній роботі над курсом.

1. Векторний аналіз

Скалярне поле - область простору, кожна точка якого характеризується деяким значенням скаляра. Так як кожна точка визначається радіусом-вектором , то поле визначається скалярною функцією . Прикладом скалярного поля є поле температур.

Якщо поле залежить від часу, то

Точки поля, де має однакові значення, утворюють поверхню, що називається поверхнею рівного рівня або еквіпотенціальною поверхнею:

Надаючи с різні значення, одержимо сімейство поверхонь, розподіл яких у просторі характеризує поле.

Вектор, чисельно рівний і направлений по нормалі до еквіпотенціальної поверхні убік зростання скаляра , зветься градієнтом скаляра, тобто

де - орт зовнішньої нормалі.

Швидкість зміни скаляра в будь-якому іншому напрямку дорівнює проекції градієнта на цей напрямок

(1.1)

Напрямок градієнта є напрямком найбільш швидкого зростання скаляра , а - напрямком найбільш швидкого убування . У напрямках дотичних до поверхні рівного рівня значення зовсім не змінюється, тобто .

Відповідно до виразу (1.1) проекції градієнта на осі декартовій системи координат:

Введемо оператор Гамільтона («набла»). Оператором називається символічне зображення сукупності математичних операцій, виконаних над функцією.

(1.2)

Тоді

(1.3)

де - складова векторного оператора , тобто

Вираз (1.3) є диференціальною характеристикою скалярного поля.

Векторне поле - область простору, кожна точка якого характеризується деяким значенням вектора. Так як кожна точка визначається радіусом-вектором , то поле визначається векторною функцією . Якщо поле залежить від часу, то . Прикладами векторних полів є магнітне, електричне і гравітаційне. Поле градієнта скалярного поля також є векторним. Векторне поле графічно можна характеризувати векторними або силовими лініями. Векторною або силовою лінією називається крива, дотична до якої в кожній точці збігається з напрямком векторного поля (рис.1).

Рис.1. Графічне уявлення векторного поля

Кожна точка кривої визначається радіусом-вектором . Дотична до кривої визначається вектором . По визначенню векторної лінії вектори і повинні бути рівнобіжні, тобто проекції цих векторів пропорційні. Отже, система

подає систему векторних ліній. Векторні лінії характеризують напрямок поля в точках, через які вони проведені. Проте за допомогою цих ліній можна характеризувати і модуль вектора, проводячи векторні лінії густіше там, де абсолютна величина вектора більше.

Диференціальними характеристиками векторного поля є:

1. дивергенція або розбіжність вектора - скалярна функція, аргументом якої є векторна функція точки, тобто

або з урахуванням (1.2) у декартовій системі координат

2. ротор або вихор вектора - векторна функція, аргументом якої є векторна функція точки.

або

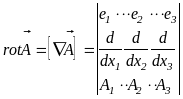
Похідні другого порядку:

(1.4)

де - оператор Лапласа (лапласіан).

У декартовій системі координат

Унаслідок рівнобіжності векторів

Унаслідок перпендикулярності векторів і .

(1.5)

З формули (1.5) слідує:

(1.6)

Деякі формули векторного аналізу.

Теорема Стокса. Циркуляція вектора по замкнутому контуру дорівнює потокові через поверхню , що обпирається на цей контур, тобто

(1.7)

Або

де - проекція на напрямок нормалі до поверхні .

Якщо поверхня настільки мала, що у всіх її точках можна вважати постійною величиною, то

Ця формула справедлива в граничному випадку нескінченно малої поверхні , тобто

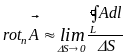(1.8)

Проекція буде найбільшої, коли збігається по напрямку з . Очевидно, напрямок вектора збігається з напрямком нормалі до площини, у якій циркуляція вектора найбільша. Модуль ротора вектора в даній точці поля дорівнює межі відношення циркуляції вектора , що проходить через цю точку і збігається з площиною, де циркуляція максимальна, до розміру площадки, коли вона стягається в цю точку. Величина характеризує обертальну здатність поля.

Теорема Остроградського-Гауса. Потік вектора через замкнуту поверхню дорівнює інтегралу від , узятому по об'єму , обмеженому цією поверхнею, тобто

(1.9)

або

де - проекція вектора на напрямок нормалі до поверхні .

Якщо поверхня настільки мала, що у всіх лежачих в середині її точках можна вважати постійною, то

Ця формула справедлива в граничному випадку нескінченно малої поверхні, тобто

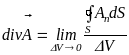(1.10)

Отже, дивергенція вектора в даній точці дорівнює межі відношення потоку вектора через замкнуту поверхню , що утримує усередині себе цю точку, до об'єму , обмеженому поверхнею , коли вона стягається в точку.

Дивергенція є скалярною величиною, що характеризує інтенсивність джерел або стоків поля. Точки поля, де , називаються стоками поля; векторні лінії сходяться до цих точок; точки, де , називаються джерелами поля, векторні лінії розходяться з цих точок. Якщо , то поле не має ні джерел, ні стоків.

Формули Гріна. Якщо , де і - скаляри, то

Підставляючи цей вираз в (1.9), одержуємо першу формулу Гріна:

(1.11)

Переставляючи і , одержимо:

Вичитаючи останній вираз з (1.11), одержуємо другу формулу Гріна:

(1.12)

Класифікація векторних полів.

Якщо , то поле вектора називається безвихровим. Якщо розглянута область є однозв'язною, то поле, що задовольняє цій умові, називається потенційним і може бути подане у виді

(1.13)

тому що . Функція називається потенційною функцією або потенціалом поля. Очевидно, що потенціал визначається неоднозначно, тому що , де - постійна, що не залежить від координат простору.

Знак мінус у виразі (1.13) обраний із тих міркувань, що векторні лінії поля направлені убік убування потенціалу.

У потенційному полі тобто існують джерела і стоки поля, а лінії поля не замкнуті. Так як відповідно до (1.4) , то скалярний потенціал задовольняє рівнянню Пуасона:

З умови (1.13) відповідно до рівності (1.7) слідує, що , тобто циркуляція вектора уздовж будь-якої замкнутої кривої дорівнює нулю. Фізично це означає, що в потенційному полі робота уздовж замкнутого контуру дорівнює нулю.

Відповідно до теореми Остроградського-Гауса (1.9)

тобто потік вектора через замкнуту поверхню не дорівнює нулю.

Поле вектора називається соленоїдальним, якщо в ньому немає джерел і стоків, тобто в будь-якій точці . Для соленоїдального поля , так як . Функція називається векторним потенціалом.

Вважаючи з урахуванням (1.6), одержимо рівняння Пуасона у векторній формі:

Відповідно до виразу (1.7) при циркуляція вектора для соленоїдального поля не дорівнює нулю

Отже, робота вектора поля уздовж замкнутого контуру також не дорівнює нулю. Цим соленоїдальне поле відрізняється від потенційного.

Відповідно до теореми Остроградського-Гауса (1.9) і визначенню соленоїдального поля маємо:

тобто потік вектора

через замкнуту поверхню дорівнює нулю. Якщо виділити в полі векторну трубку (рис.2), то з умови слідує, що в соленоїдальному полі векторні лінії є замкнутими або ідуть у нескінченність.

Рис.2. Векторна трубка.

За умови і поле вектора є безвихровим, не має джерел і стоків. Таке поле називається лапласовим, характеризується воно одночасно векторним і скалярним потенціалами , які за умови задовольняють рівнянням Лапласа

,

Функції, що задовольняють рівнянню Лапласа, називаються гармонійними.

Диференціювання в криволінійних ортогональних координатах. Положення точки М в просторі визначається радіусом-вектором , координати якого залежать від прийнятої системи координат. Положення точки в просторі можна однозначно визначити пересіченням трьох поверхонь (рис.3), які називаються координатними. Пересічення двох поверхонь дає лінію, називану координатною, значення двох координат на цій лінії постійні, а третя змінюється. Координати точки називаються криволінійними.

Рис.3. Координатні поверхні, лінії і осі ортогональної криволінійної системи координат.

Найбільше поширені ортогональні криволінійні системи, у яких дотичні до координатних ліній у кожній точці перетинаються під прямими кутами. Ці дотичні називаються координатними осями; напрямок їх змінюється від точки до точки. У загальному випадку координати точки в узагальненій криволінійній системі зв'язані з координатами прямокутної декартової системи рівняннями

обернено

У криволінійній системі координат зміна координати на , призводить до переміщення уздовж координатної лінії:

де залежить від вигляду координат і називається коефіцієнтом Ламе. Дійсно, елемент довжини координатної лінії можна записати як

де

Звідси

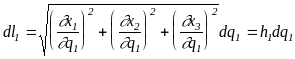
Аналогічно

На підставі цього коефіцієнти Ламе можна записати у вигляді

Інтервал між двома точками визначиться як

Елементи координатної поверхні:

Елемент об'єму

За допомогою отриманих співвідношень зробимо диференціювання в криволінійній системі координат. Відповідно до виразу (1.1) одержимо:

(1.14)

З урахуванням рівності (1.11)

(1.15)

Відповідно до (1.8)

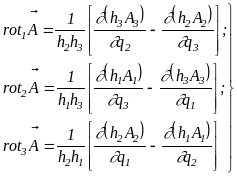(1.16)

Відповідно до виразів (1.4), (1.14) і (1.15)

(1.17)

Вирази (1.14)-(1.17), переписані в циліндричних, сферичній системах координат, мають широке застосування в теорії електромагнітного поля.

Циліндрична система координат (рис.4). Координатними поверхнями є: площини , кругові циліндри і полуплощини , що проходять через вісь під кутом до фіксованій полуплощини. Координатними лініями є: прямі , і , і окружності , . Напрямок координатних осей визначається ортами . У цій системі .

Циліндричні координати зв'язані з декартовими наступними співвідношеннями: . Коефіцієнти Ламе: .

Відповідно до формул (1.14) - (1.17) одержимо

Рис.4. Циліндрична система координат.

а—координатні поверхні; б—координатні лінії, осі я їхні орти.

Відповідно до виразу (1.6)

тут - лапласіани скалярних величин.

Сферична система координат (рис.5). Координатними поверхнями є сфери радіуса , конуси з кутом розчину і полуплощини, що проходять через вісь під кутом до фіксованої полуплощини. Координатними лініями є: окружності і і прямі . Напрямок координатних осей визначається ортами . У цій системі .

Сферичні координати. зв'язані з декартовими співвідношеннями:

Коефіцієнти Ламе: . Відповідно до формул (1.14)-(1.17) одержуємо:

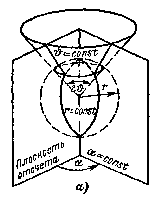
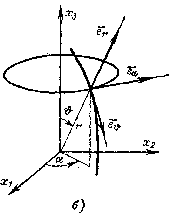
Рис.5. Сферична система координат.

я—координатні поверхні; б - координатні лінії, осі і їхні орти