22. Метод простых итераций решения функциональных уравнений и систем. Условия сходимости.

Пусть (одномерный случай) и задана функция f(x), удовлетворяющая условиям:

1) - условие Липшица с константой на отрезке [a,b]; 2) .

(1)

Тогда оператор f(x) - сжимающий и уравнение f(x)=х имеет единственную неподвижную точку, которую можно найти методом простых итераций:

.

Действительно, определим . Следовательно, выполняется условие Липшица из теоремы 3.2, откуда и следует результат.

Теорема 3.4. Пусть , причем выполнены условия:

1) ; 2)

(8)

Тогда оператор f(x) является сжимающим, и справедливо утверждение теоремы 3.1, т.е. последовательность сходится к единственному коню уравнения .

Пусть , тогда , согласно условию 1) теоремы. Далее по индукции устанавливаем, что все члены последовательности принадлежат . Пусть . Согласно теореме о среднем

, . Оценим это неравенство по модулю:

согласно условию 2) теоремы.

Таким образом, выполняются все условия теоремы 3.3., откуда и следует результат.

Рассмотрим задачу поиска корней уравнения . Пусть известны границы для единственного корня этого уравнения и мы хотим найти этот корень методом итераций. Если удастся привести уравнение к виду x=f(x), так чтобы выполнялись условия теоремы 3.3 или теоремы 3.4, то в этом случае можно будет применить метод итераций. Такое преобразование, вообще говоря, не единственно, причем главная трудность заключается в определении того замкнутого ограниченного множества S (а в одномерном случае – отрезка [a,b]), для которого помимо условия сжатости, выполняется условие .

Лемма 3.1. Определим множество - замкнутый r-“шар” с центром в точке х₀ (в одномерном случае – отрезок). Пусть оператор Т - сжимающий на S и выполняется следующее условие:

(9)

Тогда для любой точки выполняется: .

Достаточно доказать, что Имеем: {неравенство треугольника} .

23. Метод Ньютона. Геометрическая интерпретация. Теорема о сходимости метода в одномерном случае.

Пусть снова задано уравнение f(x)=0. Запишем его в виде ,

где положим . Пусть х_к – некоторое приближение к корню х*. Для ускорения сходимости итераций желательно, чтобы был как можно меньше. Положим Отсюда находим, что 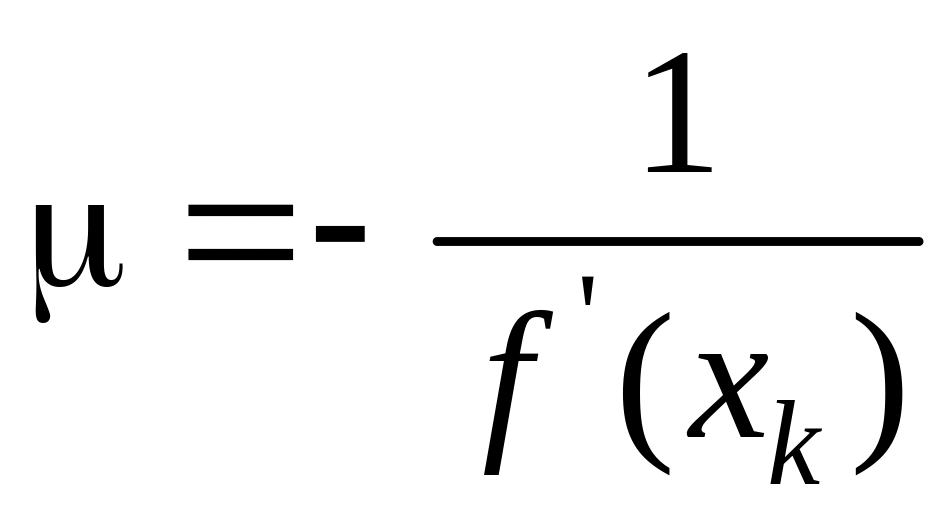. Подставляя в исходное уравнение, получаем рекуррентную формулу:

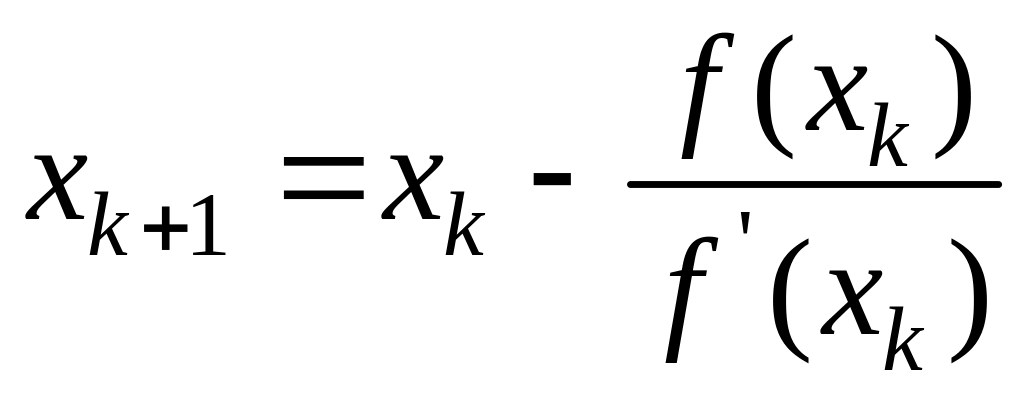, (11)

Это и есть итерационная процедура Ньютона.

Метод Ньютона известен и под другим названием: метод касательных. Дадим графическую иллюстрацию данного метода. Пусть и строго выпукла (т.е. ). Пусть, кроме того, - единственный корень функции на промежутке .

В качестве начального приближения возьмем точку , такую, для которой . Проведем через точку на плоскости касательную к кривой . Запишем уравнение касательной: . В качестве следующего приближения возьмем точку , в которой . Отсюда находим . Далее в точке графика проводим новую касательную, и т.д. В результате получаем итерационную процедуру Ньютона (11).

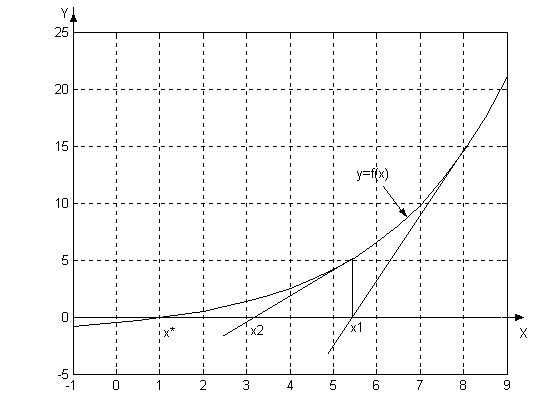
Метод касательных проиллюстрирован на рис.3.2.

Рис.3.2. Графическая иллюстрация метода Ньютона (метода касательных).

Начальная точка x₀ = 8. Точное значение корня x* = 1. x₁ и x₂ – два последовательных приближения к корню, полученные с помощью касательных.

Исследуем условия сходимости метода Ньютона.

Теорема 3.5. Пусть , на , и имеет единственный действительный корень на . Тогда , такое, что на множестве

процедура Ньютона (1) сходится к точке со скоростью геометрической прогрессии, а в некоторой малой окрестности точки x^* и с квадратичной скоростью.

В силу непрерывности функций на [a,b], обе производные ограничены поэтому , причем по условию.

Заметим, что итерационная процедура (11) равносильна методу простых итераций для уравнения 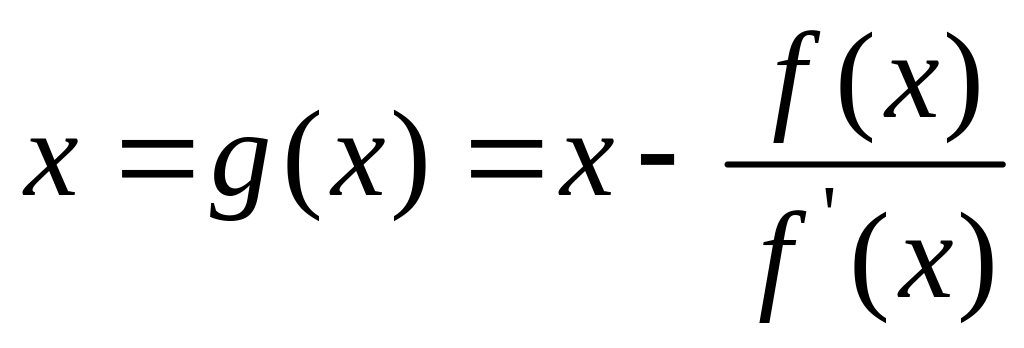(12)

Очевидно, что является неподвижной точкой функционального оператора , называемого операторной функцией Ньютона-Рафсона. Проверим условия сжатости данной функции. Для этого вычислим и оценим производную . Имеем:

.

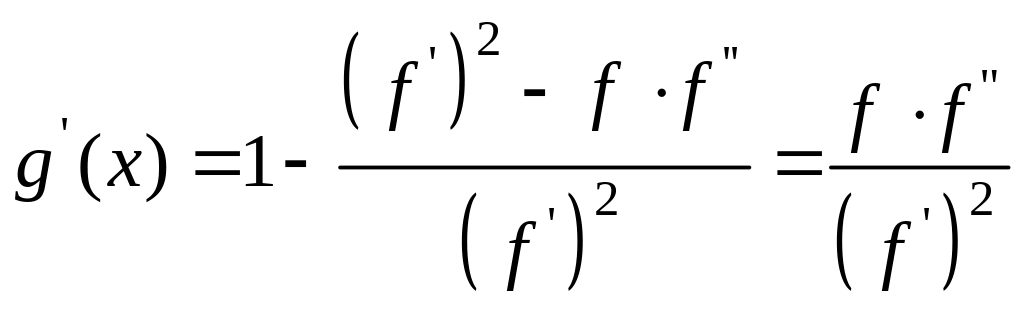Оценивая полученное равенство по модулю, и учитывая условия теоремы, получим 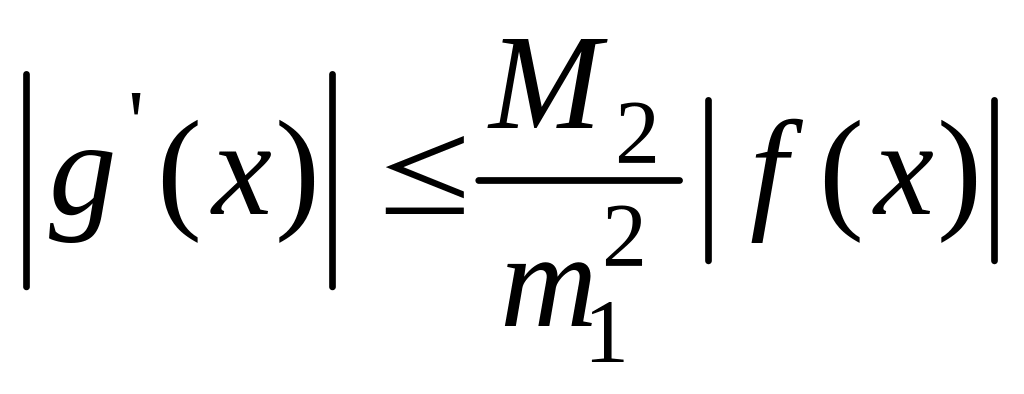(13) Поскольку - корень уравнения , то, как следует из неравенства (13), и близка к нулю в некоторой малой окрестности точки , где и следует ожидать выполнения условия сжатости. Запишем формулу конечных приращений Лагранжа .

Оценивая по модулю, получаем .

Подставляя эту оценку в (13), получаем: .

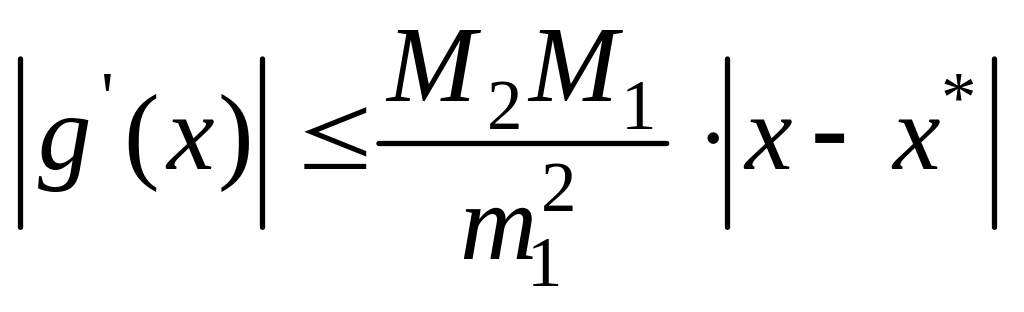Условие сжатости будет, очевидно, выполнено, если

. (14)

Обозначив 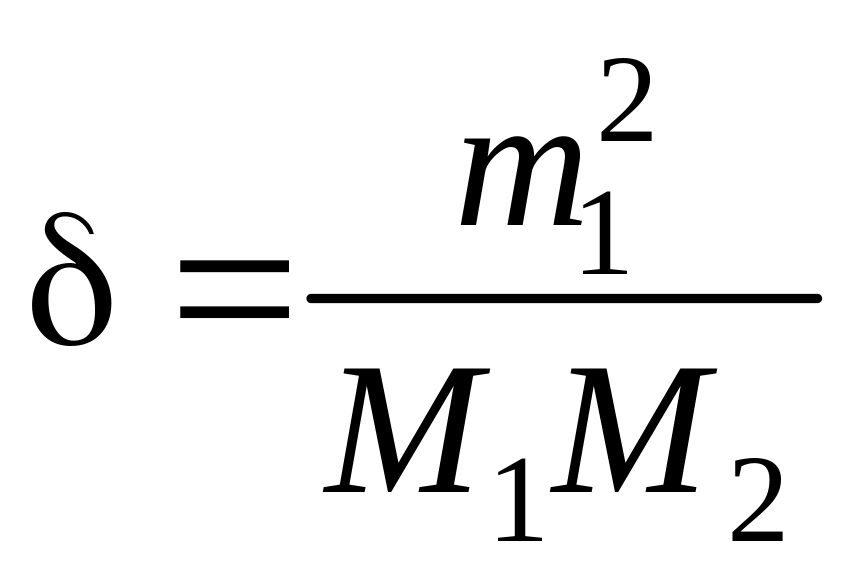, получаем конкретизацию окрестности , где выполняется одно из условий сжатости. Пусть теперь найдено -е приближение к корню .

Так как по условию теоремы непрерывна на , то справедливо тэйлоровское разложение функции с центром в точке с остаточным членом в форме Лагранжа

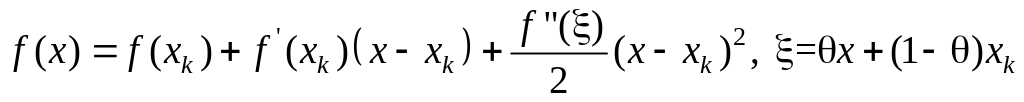
Положим в последнем равенстве : .

Выражая отсюда , получим: 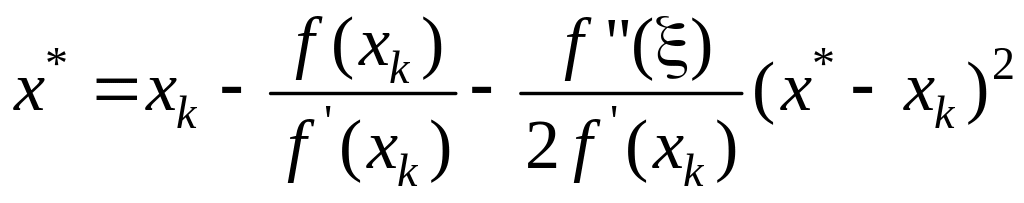(15)

Вычтем (15) из (11): ;

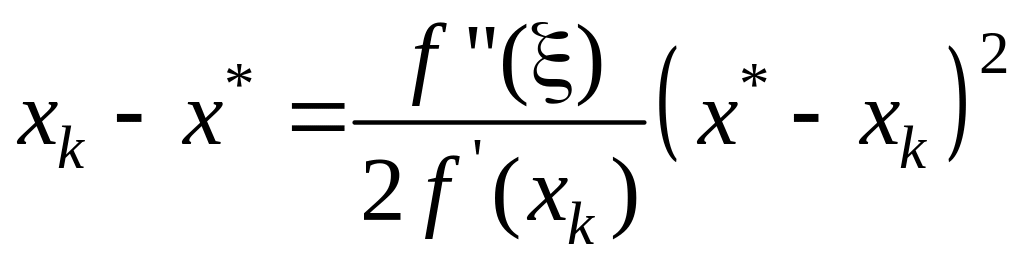Оценивая последнее равенство по модулю, получаем: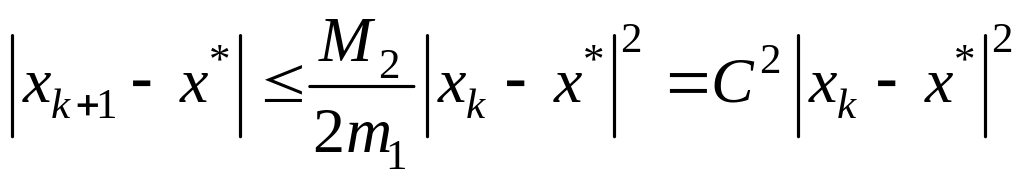 (16)

Продолжим далее оценку по модулю, используя (14):

.

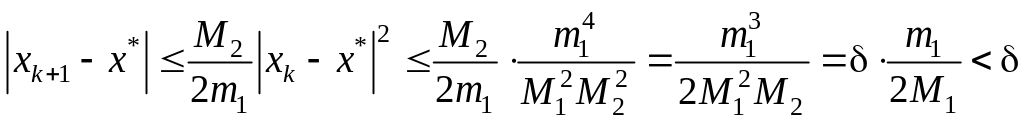Таким образом, если , где определяется из неравенства (14), то точка . Следовательно, выполняется и второе условие теоремы 3.4, а значит последовательность сходится к корню со скоростью геометрической последовательности (т.е. линейно). Далее из неравенства (16) следует, что как только при некотором выполнится условие , так в дальнейшем, при сходимость становится квадратичной:

.