
- •2. Позиционная и нормализованная формы записи чисел. Значащие и верные цифры позиционной системы.
- •3. Ошибки округления чисел. Распространение ошибок округления в арифметических операциях. Абсолютная и относительная погрешность суммы, разности, произведения и частного.
- •Определение 2. Величина называется абсолютной погрешностью представления числа X с помощью числа .
- •4. Близость в метрическом и нормированном пространствах. Расстояние и норма, их определения и свойства. Основные классы функций:
- •5. Постановка задачи интерполяции. Интерполяционный многочлен Лагранжа. Теорема о погрешности интерполяции. Единственность многочлена Лагранжа.
- •6. Интерполяция на равномерной сетке. Конечные разности и их свойства.
- •1) Докажем, что операторы и перестановочные. .
- •7. Интерполяционный многочлен Ньютона. Построение и оценка погрешности.
- •8. Ортогональность в гильбертовом пространстве. Многочлены Чебышёва. Определение, построение, свойства.
- •9. Применение многочленов Чебышёва к задаче интерполяции. Теорема об оптимальном выборе узлов.
- •10. Среднеквадратичное приближение функций. Постановка задачи, теорема о существовании и единственности.
- •20. Классические ортогональные многочлены. Построение ортогональных многочленов на каноническом отрезке [-1,1].
- •11. Численное интегрирование. Использование функциональных рядов.
- •12. Квадратурная формула на основе интерполяции. Формулы дл коэффициентов и остаточного члена.
- •13. Базовые квадратурные формулы прямоугольников, трапеций и парабол. Формула теоретической погрешности.
- •14. Обобщенные квадратурные формулы трапеции и Симпсона (формулы Ньютона-Котеса).
- •15. Теоретич. Оценки погрешности обобщённых формул трапеции и Симпсона.
- •16. Правило Рунге практической оценки погрешности квадратурной формулы Симпсона.
- •17. Общие свойства полиномов ортогональных с весом.
- •18. Алгебраическая степень точности квадратурной формулы. Квадратурные формулы Гаусса-Кристоффеля.
- •19. Теорема о необходимых и достаточных условиях выбора узлов в формулах Гаусса-Кристоффеля.
- •21. Принцип сжатых отображений. Теорема о неподвижной точке. Доказать единственность неподвижной точки. Следствия теоремы для банаховых пространств и пространства
- •22. Метод простых итераций решения функциональных уравнений и систем. Условия сходимости.
- •23. Метод Ньютона. Геометрическая интерпретация. Теорема о сходимости метода в одномерном случае.
- •24. Метод Ньютона в многомерном случае. Организация итерационного алгоритма.
- •25. Численные методы решения слау. Прямые и итерационные методы, общие понятия.
- •26. Нормы вещественных квадратных матриц. Спектральные свойства матриц.
- •27. Обусловленность матриц и систем лау. Число обусловленности в спектральной норме.
- •28. Метод итераций для слау специального вида. Теорема о достаточных условия сходимости.
- •29. Спектральный признак сходимости.(теорема о необх. И дост. Усл. Сходимости)
- •30.Стационарные итерационные процедуры. Приведение слау к системе специального вида.
- •31. Метод простых итераций Ричардсона. Условия сходимости.
- •32. Теорема о выборе ускоряющего множителя в методе Ричардсона.
- •33. Метод Якоби. Организация алгоритма. Теорема о достаточных условиях сходимости.
- •34. Метод Зейделя как ускорение метода Якоби. Организация алгоритма. Теорема об условиях сходимости.
- •35. Метод последовательной верхней релаксации. Задача выбора ускоряющего множителя.
- •36. Численное дифференцирование на основе интерполяции.
- •37. Численное дифференцирование на равномерной сетке, основанное на тэйлоровском разложении. Теорема об аппроксимации первой и второй производной.
- •38. Задача Коши. Постановка задачи. Сведение к системе для уравнения n-ого порядка.
- •39. Метод Эйлера. Алгоритм, геометрическая интерпретация, порядок точности.
- •40. Методы Рунге-Кутты повышенной точности. Метод «предиктор-корректор» и метод «средней точки».
- •41. Общая постановка краевой задачи для решения оду второго порядка. Классификация граничных условий.
- •42. Метод «стрельбы» решения краевой задачи с граничными условиями первого рода.
- •43. Метод конечных разностей решения линейной краевой задачи для оду второго порядка.
- •44. Каноническая разностная схема для линейного оду второго порядка, имеющая порядок аппроксимации .
- •45. Устойчивость разностных схем. Спектральный признак устойчивости для уравнений с постоянными коэффициентами. Примеры для оду и уравнений в частных производных.
1. Структура погрешности в численном анализе.
Рассмотрим основные источники погрешностей, возникающих в численном анализе.
Погрешности математической модели.
Любая задача есть модель какого-то явления. Всякая модель – это объект более простой, чем реальный. Модель – приближенное описание реального объекта, т.е. содержит погрешности.
Погрешности исходных данных.
Данные могут оказаться неточными в результате неточных измерений или ввода в компьютер таких констант как π, е и др.
Погрешности метода решения.
Численные методы заменяют задачу на близкую. Например, вместо интегрирования – суммирование, вместо дифференцирования – вычисление конечно разностного отношения и т.д. В результате вместо точного решения исходной задачи получаем приближенное решение преобразованной задачи.
Погрешности округлений при выполнении арифметических операций.
В рамках численных методов погрешности 1 и 2 считаются неустранимыми. Погрешность метода обычно оценивается в норме того метрического пространства, в котором действуют операторы преобразованной задачи. Чаще всего алгоритм решения устроен как итерационный процесс. Поэтому возникает проблема сходимости этого процесса к некоторому решению – приближенному решению исходной задачи и вопрос о близости полученного решения к точному решению исходной задачи.
Рассмотрим подробнее пункт 4 – ошибки округления.
Ошибки округления связаны с устройством арифметического процессора на ЭВМ, имеющего конечную разрядность.
2. Позиционная и нормализованная формы записи чисел. Значащие и верные цифры позиционной системы.
Ошибки округления связаны с устройством арифметического процессора на ЭВМ, имеющего конечную разрядность. Чтобы разобраться в этом вопросе, рассмотрим две основные формы записи чисел.
1) Запись числа в позиционной системе счисления:
![]() ,
где a
– основание позиционной системы,
a
,
где a
– основание позиционной системы,
a![]() {2,8,16,10,…},
{2,8,16,10,…},![]() .
.
Определение 1. Значащими называются все цифры числа X, записанного в позиционной системе, начиная с первой слева отличной от нуля.
2) Нормализованная форма записи числа (запись числа в арифметическом процессоре «с плавающей запятой»):
![]() ,
где f –
мантисса числа X,
удовлетворяющая условию
,
где f –
мантисса числа X,
удовлетворяющая условию
![]() ,
а
- основание системы счисления (а=2,8,10
и т.д.), L
– порядок числа,
,
а
- основание системы счисления (а=2,8,10
и т.д.), L
– порядок числа,
![]() ,
,
![]() ,
,
![]() - цифра в k-ом
разряде мантиссы (дробного числа),
- цифра в k-ом
разряде мантиссы (дробного числа),
![]() ,
k=2,3,…
, 0< f1<a,
t
– число используемых значащих цифр
(характеристика вычислительного
устройства).
,
k=2,3,…
, 0< f1<a,
t
– число используемых значащих цифр
(характеристика вычислительного
устройства).
Определение 4.
Значащая цифра αj
числа X,
записанного
в позиционной системе, называется верной
в широком смысле,
если выполняется условие Δ(X*)![]() a
j
и верной
в узком смысле,
если выполняется условие Δ(X*)
0,5*a
j.
a
j
и верной
в узком смысле,
если выполняется условие Δ(X*)
0,5*a
j.
В дальнейшем курсе будет использоваться главным образом понятие верной цифры в широком смысле.
Если вводимое в ЭВМ число X (или полученное на каком либо этапе вычислительного процесса) имеет число значащих цифр мантиссы, превышающее значение t, то происходит так называемое округление числа. В компьютерах обычно реализовано симметричное округление по следующему правилу: если в старшем из отбрасываемых разрядов стоит цифра меньшая пяти, то содержимое сохраняемых разрядов числа не изменяется. В противном случае в младший сохраняемый разряд добавляется единица с тем же знаком, что и у самого числа. Кратко это правило формулируют так: округление до ближайшего целого.
3. Ошибки округления чисел. Распространение ошибок округления в арифметических операциях. Абсолютная и относительная погрешность суммы, разности, произведения и частного.
Ошибка округления, будучи внесенной на каком либо этапе вычислительного процесса, начинает распространяться во всех последующих операциях. Таким образом, в конечный результат будет внесена результирующая ошибка округления.
Определение 2. Величина называется абсолютной погрешностью представления числа X с помощью числа .
Максимально
возможное значение
![]() ,
т.е. число
,
т.е. число
![]() ,
удовлетворяющее неравенству
,
удовлетворяющее неравенству
![]() ,
называется максимальной
или предельной
абсолютной
погрешностью
(ошибкой).
,
называется максимальной
или предельной
абсолютной
погрешностью
(ошибкой).
Определение 3.
Величина,
равная
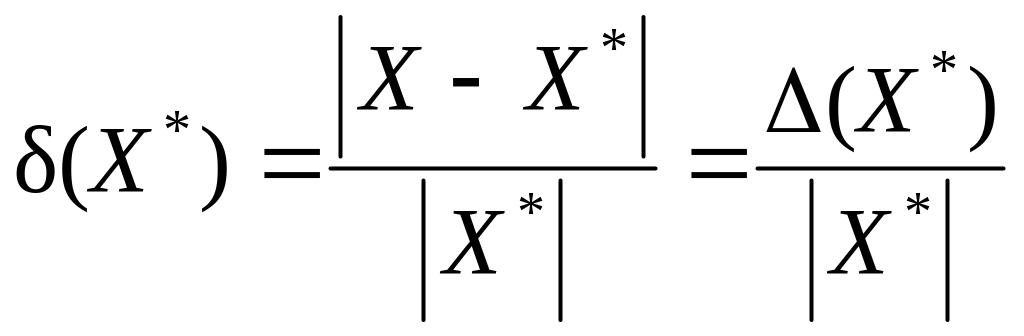 ,
,
называется относительной ошибкой представления числа X числом .
Если
![]() ,
то число
,
то число
![]() называется максимальной
предельной относительной ошибкой.
называется максимальной
предельной относительной ошибкой.
Распространение ошибок округления в арифметических операциях.
1) Операции сложения и вычитания.
Пусть
![]() ,
,
![]() .
Тогда
.
Тогда![]() ,
где
,
где
![]() .
Поскольку
.
Поскольку
![]() ,
то
,
то
![]() ,
,
т.е. при сложении чисел предельные абсолютные ошибки складываются.
Не трудно убедиться, что такое же правило справедливо и для разности.
2) Операция умножения.
Пусть![]() ,
где
,
где
![]() ,
,
тогда![]() ,
,
Следовательно,
![]() ,
,
т![]() .е.
.е.
![]() .
.
Если последнее слагаемое имеет второй порядок малости по сравнению с первыми двумя, то им можно пренебречь. В этом случае получаем более простое правило: при умножении относительные максимальные ошибки приближенно складываются.
3)
Операция
деления.
Пусть
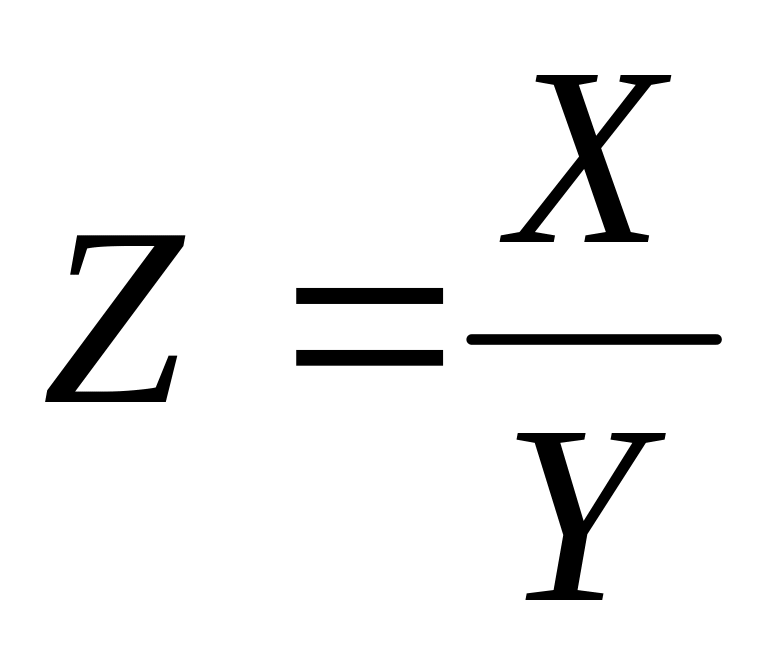 ,
,
.
,
,
.
![]() Пример
4.
Показать, что справедливо следующее
правило:
Пример
4.
Показать, что справедливо следующее
правило:
![]() .
.
