
Лекция 1. Приближенные вычисления.
Структуры погрешности в численном анализе.
Численное решение прикладных задач всегда интересовало математиков. Названия некоторых численных методов носят имена крупнейших ученых своего времени: Ньютона, Эйлера, Лобачевского, Гаусса, Чебышева, Эрмита и других.
Наше время характерно резким расширением приложений математики, связанное с появлением ЭВМ. Менее чем за пятьдесят лет скорость выполне-
ния арифметических операций возросла от 0,1с при ручном счете до 1012 опе-
раций на современных серийных ЭВМ, т.е. примерно в 1013 раз. Рост возможностей в связи с созданием вычислительной техники сравнивают с промышленной революцией, вызванной изобретением паровой машины. Заметим, что в результате промышленной революции и последующего развития науки и техники скорость передвижения возросла от скорости пешехода 6 км/ч до скорости космонавта 30000км/ч, т.е. в 5000 раз.
С помощью современных компьютеров удалось решить много важных на- учно-технических задач. Например, успехи в решении атомных и космических проблем вряд ли были бы возможны без применения компьютеров и численных методов.
Расширение возможностей приложения математики привело к математизации химии, биологии, экономики, психологии, медицины и др. Суть математизации состоит в построении математических моделей процессов и в разработке методов их исследования.
Достижения в применении ЭВМ обусловлены взаимосвязанным сочетанием ряда следующих факторов, без пропорционального развития которых успехи были бы намного скромнее:
1.увеличение быстродействия ЭВМ;
2.разработка программных средств (общения с ЭВМ);
1
3.рост понимания процессов и явлений науки и техники, природы и общества и создание их математических моделей;
4.создание методов решения новых задач;
5.рост понимания возможностей и координация усилий специалистов (различных профилей).
Здесь пункты 3. и 5. определяют, какие задачи решать, пункты 2. и 4. как их решать, пункты 1. и 2. - это технические и программные средства. Необходимым является уверенное освоение материала, обозначенного пунктами 2. и 4., но надо стремиться и к решению проблем, обозначенных пунктами 3. и 5.
Рассмотрим следующие примеры.
1.В курсе математического моделирования на мощных 600 МГц компьютерах с помощью ode45 удавалось получить только одно-двумерные максимально упрощенные зависимости. На БЭСМ-6 (0,5 млн. опер./с) возможно рассчитывать сложные двумерные конвективные течения жидкости и газа, благодаря эффективному численному методу, который актуален и сегодня.
2.Ярким примером является холодная война. Западные ЭВМ были на порядок и более быстрыми. Но у советских ученых были лучше численные методы. За счет этого был паритет.
3.Решение дифференциальных уравнений в частных производных приводит к необходимости решать системы линейных алгебраических уравнений, в каждой строке которой 5-10 ненулевых элементов. До появления ЭВМ их ре-
шали для числа неизвестных 10 −102 Сейчас благодаря новым численным ме-
тодам решают для 105 −106 неизвестных.
Если бы на современных ЭВМ решали численными методами 30-летней давности, то смогли бы решать только для 103 −104 неизвестных.
Структура погрешности в численном анализе.
Основные источники погрешностей:
1. Погрешность математической модели. Любая задача есть модель како- го-то явления. Всякая модель - это объект более простой, чем реальный. Мо-
2
дель - это приближенное описание реального объекта, т.е. содержит погрешности.
2.Погрешности исходных данных. Данные могут оказаться неточными.
3.Погрешности метода решения. Численные методы заменяют задачу на близкую. Например, вместо интегрирования - суммирование, вместо дифференцирования - вычисление конечно-разностных отношений. В результате вместо точного решения исходной задачи получаем приближенное решение преобразованной задачи.
4.Погрешности округлений при выполнении арифметических операций.
Врамках численных методов погрешности 1. и 2. являются неустранимы-
ми.
Пример.
Рассмотрим многочлен
P(x)= (x −1)(x − 2)...(x − 20)= x20 − 210x19 + 20615x18 +... ;
Очевидно, его корнями являются x1 =1; x2 = 2;...; x20 = 20.
С помощью встроенных в MATLAB функций легко убедиться, что корни находятся верно.
P = poly(1:20) - коэффициенты полинома, корнями которого являются аргументы функции
roots(P) – нахождение корней полинома.
Если изменить, например, значение 2-го коэффициента на величину 10−7
(что составляет ~ 5 *10−8% % от числа), то половина корней станут комплексными. Малые погрешности приводят к качественно новому результату – уходу корней с действительной оси в комплексную плоскость.
Следует ясно понимать, что численные методы являются по своей сути приближенными, с помощью которых принципиально нельзя получить точный результат, даже если численный метод является точным.
Пункты 1. и 2. приводят к неустранимым погрешностям. Пункт 4., связанный с ограниченной разрядной сеткой компьютера (бесконечные дроби пред-
3
ставлены в конечном виде), также приводит к неустранимым погрешностям, за исключением физически мало интересного случая работы с целыми числами.
Рассмотрим представление числа в компьютере. Число формата double - 64-разрядное число (8 байт), в котором 1 бит - знаковый, 52 отводятся под мантиссу и 11 под порядок числа.
D = ±m 2n , m = 0.m m |
...m |
k |
, m ≠ 0 - мантисса числа, n - порядок. |
|
1 2 |
|
1 |
|
|
Максимальное число 1.8 10308 |
- машинная бесконечность. |
|||
Минимальное число 2.2 10−308 |
- машинный нуль. |
|||
Мантисса содержит 15-16 десятичных знаков. Все, что выходит за эти пределы будет отброшено.
Казалось бы, такая точность представления способна удовлетворить любые нужды исследователя. Однако необходимо помнить, что, например, перед тем как два числа будут сложены, они должны быть приведены к единому порядку, а то, что при сложении выйдет за мантиссу будет отброшено. Поэтому,
если сложить108 +10−7 ,то в мантиссу уложатся 15 десятичных знаков и будет получен верный результат, а если выполнить108 +10−8 , то малое число выйдет
за разрядную сетку, и получим те же108 .
Если прибавить к 1 малое число10−16 ,но последовательно 1017 раз (такие вычисления характерны для задач ЧМ - вычисление рядов, разнообразные итерационные, разностные задачи…). Легко найти ответ - 11, однако, машинная арифметика дает 1 – ошибка 1000%! Если сначала найти сумму малых величин, а потом прибавить к 1, то результат будет верный. Таким образом, машинное сложение, в общем случае не коммутативно.
Знание этих фактов позволяет протестировать компьютер на погрешность
вычислений. Найдем значение выражения |
S = |
1 + ε −1 |
приε = 2−n , n = 0,1,2... . С |
||||||
ε |
|
||||||||
|
|
|
|
|
|
|
|||
точки зрения аналитической математики S =1 всегда, |
но в компьютере, начи- |
||||||||
ная с некоторогоn , S = |
1 + ε −1 |
= |
1 −1 |
= 0 . |
|
|
|
|
|
ε |
|
|
|
|
|
||||
|
|
ε |
|
|
|
|
|||
4

Замечание.
Если быS = 1 −1ε+ ε , то S было бы равно 1 всегда и в ЭВМ.
Нетрудно понять, почему операция вычитания близких (и тем более больших по величине) чисел чревата неприятностями при машинных вычислениях.
Представим себе два близких по величине числа:
x = 0.abcdefg y = 0.abcde1 f1g1 .
Т.о., x и y отличаются друг от друга пятой и далее (после десятичной точ-
ки) цифрами. Разность этих чисел будет величиной ~10−5 (efg − e1 f1 g1 ). Допус-
тим, что цифры f и f1 далее искажены за счет погрешности округления. То-
гда в (x − y) получим только 1 правильную цифру(e − e1 ), т.е. ошибка результа-
та на данной арифметической операции резко возрастает. Если же и цифры e и e1 неверны, то результат не имеет ничего общего с правильным решением.
Пример. (Погрешность численных методов пункт 3. и ошибка округления 4.) Пусть надо решить систему уравнений
|
−7 |
x1 |
+ x2 |
=1 |
10 |
|
|||
|
|
|
|
|
|
x1 + 2x2 = 4 |
|||
|
||||
1 метод.
Исключим x1 из первого уравнения: x1 =107 −107 x2 ; подставим во второе уравнение
x2 |
= |
107 |
− 4 |
. |
|
|
|||
|
107 |
− 2 |
||
Если считать с семью значащими цифрами, то
x2 =1.000000 x1 = 0.000000
(что совершенно неверно, как следует из 2-го уравнения) 2 метод.
Исключая |
|
x1 из 2-го уравнения, x1 = 4 − 2x2 ; подставляя в пер- |
||||
воеx2 |
= |
1 |
− 4 |
10 |
−7 |
. |
|
− 2 |
10 |
|
|||
|
1 |
−7 |
||||
5
При вычислении с семью значащими цифрами получим
x2 =1.000000 x1 = 2.000000
(правильный результат).
Привлечем аппарат математического анализа к исследованию влияния ошибок входных данных на результат вычислений.
|
|
Пусть вычисляется величинаφ(x, y). |
|
||||||||||||||||||||||||||||||||||||
|
|
При неточных входных данных: x = x ± x; y = y ± y ; ошибка результата |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
~ |
||
оценивается сверху следующим образом: |
|
||||||||||||||||||||||||||||||||||||||
|
|
φ≤ |
|
|
~ ~ |
|
|
|
y) |
|
≤ |
|
∂φ |
|
|
|
|
x |
|
+ |
|
∂φ |
|
|
|
y |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
φ(x, y )− φ(x, |
|
|
∂x |
|
|
|
|
|
|
∂y |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
Объективной |
мерой |
погрешности |
является относительная ошибка |
||||||||||||||||||||||||||||||||||
δ = |
|
φ |
|
= |
|
|
φ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
φ |
|
|
φ(x, y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Но как раз φ(x, y) не известна и именно ее надо вычислить. |
|||||||||||||||||||||||||||||||||||||
|
|
Обычно полагают |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
φ |
|
|
|
|
1 |
|
|
∂φ |
|
|
|
|
|
|
|
|
∂φ |
|
|
|
|
|
|
|
|
~ ~ |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
δ = |
|
~ |
≤ |
|
|
|
|
|
|
|
|
|
|
|
x |
+ |
|
|
|
|
|
y |
|
|
|
, где φ(x, y ) - вычисленный результат. |
|||||||||||
|
|
|
|
|
|
~ ~ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
φ |
|
|
φ(x, y ) |
|
|
∂x |
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Рассмотрим погрешности численных методов. Построим алгоритм вычисления интеграла
1
I n = ∫xne x−1dx, n =1,2,3... . Интегрируя по частям, находим:
|
0 |
|
|
|
|
|
|
1 |
|
|
1 |
|
e |
|
∫ |
|
|
∫ |
|
|
I1 = |
|
xe x−1dx = xe x−1 |
|10 − |
|
e x−1dx = |
1 |
0 |
0 |
|
||||
|
|
|
|
|
||
|
1 |
|
|
|
1 |
|
I 2 = ∫x2e x−1dx = x2e x−1 |10 −2∫xe x−1dx =1 − 2I1 и т.д.
0 |
0 |
1 |
1 |
I n = ∫xn e x−1dx = xn e x−1 |10 −n∫xn−1e x−1dx =1 − nIn−1 |
|
0 |
0 |
Заметим, что подынтегральная функция на всем отрезке интегрирования неотрицательна, следовательно, и значение интеграла - положительное число. Более того, подынтегральная функция на данном интервале ограничена функ-
6
цией y =1, т.е. значение интеграла не может превышать единицы. Однако если вычислить по этой формуле значение интеграла до результат будет неверным.
I n ~ n!- это очень быстро растущая функция.
∞ |
en |
|
|
|
|
|
|
|
|
|
|
|
|
|
Например, ряд ∑ |
сходится. |
|
|
|
|
|
|
|||||||
n! |
|
|
|
|
|
|
||||||||
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
un+1 |
|
|
en+1 |
|
|
n! |
|
e |
|
|
|||
По признаку Даламбера |
|
= |
= |
→ 0 , приn → ∞ . |
||||||||||
un |
(n +1)! |
en |
n +1 |
|||||||||||
|
|
|
|
|
|
|
||||||||
Поэтому предложенный алгоритм вычислений интеграла In неэффекти-
вен.
7
Лекция 2.
Численное решение нелинейных уравнений.
Пусть задана функция f (x). Задача состоит в нахождении корней уравне-
ния:
f(x)= 0 (1)
Вданном случае будем рассматривать нахождение только действительных корней.
Решение задачи разбивается на два этапа:
1.Локализация корней - выделение отрезков, на которых находится не более одного корня.
2.Поиск корня с заданной точностью.
Локализация корней выходит за рамки вычислительной математики. Можно использовать средства математического анализа. Впрочем, на этом этапе можно воспользоваться компьютером для построения таблицы значений функции f (x) или построить график этой функции.
Общего решения этой задачи нет. Оно возможно только в случае представления функции в качестве многочлена.
Рассмотрим в качестве функции f (x) полином:
f (x)= x3 − 3x2 − 9x − 5 .
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
||
Известно, что корни полиномаPn (x)= ∑ak xk , в общем случае комплекс- |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
k =0 |
|
|
|
|
|
|
|
|
|
|
|||
ные, лежат внутри круга |
|
x |
p |
|
≤1 + |
|
1 |
max( |
|
a |
0 |
|
, |
|
a |
|
,..., |
|
a |
n−1 |
|
). Таким образом, мы |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
an |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
применили аналитический подход к сужению области нахождения корней. Можно написать файл - функцию f.m и построить график функции на от-
резке[−10;10] .
Рассмотрим функцию f (x)= (x − 5)(x +1)2 . Данная функция имеет корни одинарной x = 5 и двойной x = −1 кратности.
Можно записать вектор p =[1; −3; − 9; − 5] и найти его корни, выполнив ко-
манду roots(p).
8
5.000
Врезультате будут найдены корни: −1.000 + 0.000i , т.е. эта процедура нахо-
−1.000 + 0.000i
дит все, и действительные и комплексные корни полинома.
Однако, при нахождении корней полинома Уилкинсона P(x)= (x −1)(x − 2)...(x − 20), в ответе получаем x20 = 20.0003 , что говорит об отклонении от верного результата при использовании данных команд.
Также в Matlab для решения уравнения, не обязательно полинома, служит функция fzero(‘имя файл - функции’, начальное приближение).
К сожалению, функция fzero требует, чтобы при переходе через корень функция меняла знак.
Например, с ее помощью можно найти корень уравнения бом начальном приближении, но нельзя найти корни уравнений
или f (x)= sin(x)+1 = 0 даже при самом близком начальном приближении.
В случае полинома f (x) = x3 −3x2 −9x −5 = 0 можно найти корень корень x = −1 найден не будет.
Так работают встроенные в Matlab функции. Их существование значительно облегчает решение многих уравнений, однако основная задача курса численных методов - научиться выполнять все операции над функциями без использования встроенных процедур, и лишь после этого привлекать встроенные в Matlab функции, сравнивая полученные результаты.
Рассмотрим задачу нахождения корня уравнения f (x) = 0 с заданной точ-
ностью ε , принадлежащего отрезку [a;b], методами вычислительной матема-
тики. Пусть корень некратный. Рассмотрим 3 метода:
1.Метод половинного деления (дихотомия).
2.Метод Ньютона.
3.Метод пробных итераций.
Метод половинного деления (метод дихотомии). Самый простой метод. Состоит в следующем:
9

1.Делим отрезок [a;b]пополам: c = a +2 b .
2.Проверяем знаки f (a), f (b), f (c) , выясняем, какой половине исходного отрезка принадлежит корень. Например, если f (a) > 0, f (c) > 0, f (b) < 0 , то корень
уравнения x* [c,b] .
3. Эту половину снова делим пополам, и т.д., до тех пор, пока не выпол-
нится условие b − a ≤ ε, где n - число проведенных делений исходного отрезка
2n
пополам.
4. После этого любую из границ последнего отрезка можно взять в качест-
ве ответаx ; x − x* ≤ ε .
Замечание.
Очевидно, что метод половинного деления работает, если при переходе через корень функция f (x) меняет знак, т.е. он может быть использован для вычисления корней только нечетной кратности: однократный (простой) корень, трехкратный и т.д.
Замечание 2.
В методе дихотомии ошибка на каждом шаге уменьшается в два раза,
|
x |
n+1 |
− x |
|
≤ |
1 |
|
|
|
x |
n |
− x |
|
|
≤... ≤ |
1 |
(b − a), т.е. со скоростью геометрической прогрес- |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
||||||||||||
|
|
* |
|
|
2 |
|
|
|
|
|
* |
|
2n+1 |
|
|||
|
|
|
|
|
|
|
|
|
|
||||||||
сии, где |
|
q = |
|
1 |
. |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
Таким образом, чтобы получить четыре точные цифры результата, надо выполнить столько делений исходного отрезка пополам, что-
бы |
1 |
(b − a)≤ |
1 |
10−4 |
n ≥ |
[4 + lg(b − a)]. |
|
2 |
|||||
2n+1 |
|
|
|
lg 2 |
||
Например, если b − a =1, получимn ≥14 .
Такие вычисления занимают много времени, особенно если они выполняются для каждого значения другой координаты и на каждом шаге по времени. Правда, в ходе итерационного процесса необходимо вычислять только одно значение функции f (x), не вычисляя никаких производных.
10

Метод Ньютона.
Если известно достаточно хорошее начальное приближение к решению уравнения f (x)= 0 , то эффективным методом повышения точности является
метод Ньютона.
Идея этого метода заключается в том, что в окрестности имеющегося приближения x0 задача заменяется некоторой вспомогательной линейной зада-
чей.
Эта линейная задача выбирается так, чтобы погрешность замены имела более высокий порядок малости, чем изначальный (в окрестности имеющегося приближения). За следующие приближения принимается решение этой
вспомогательной задачи. |
|
В случае скалярного уравнения |
f (x)= 0 (а можно рассматривать и систему |
нелинейных уравнений), функцию |
f (x) можно линеаризовать в окрестности |
точкиx0 , представив ее в виде отрезка ряда Тейлора:
f (x)≈ f (x0 )+ f ′(x0 )(x − x0 )+ O((x − x0 )2 ), гдеO((x − x0 )2 )≤ C(x − x0).
И вместо нелинейного уравнения решим линеаризованное уравнение: f (x0 )+ f ′(x0 )(x − x0 )= 0 , трактуя его решение как следующее (т.е. первое)
приближение к искомому значению корня.
Получим x1 = x0 − |
f (x0 ) |
. |
|
||
|
f ′(x0 ) |
|
Продолжая этот процесс, придем к формуле Ньютона:
xn+1 = xn − |
f (xn ) |
(2) |
f ′(xn ) |
для последовательности приближений к искомому решению. Рассмотрим геометрическую интерпретацию метода Ньютона в случае
решения скалярного уравнения f (x)= 0 .
Для получения xn+1 геометрически надо найти абсциссу точки пересече-
ния с осью Ox касательной к кривой y = f (x) в точке (xn , f (xn )) (рис. 2.1)
11
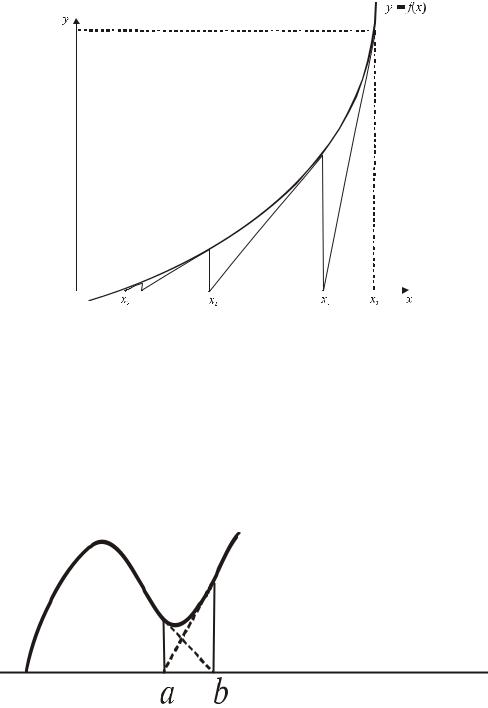
Рис.2.1 Геометрическая интерпретация метода Ньютона
y(x1 )= y(x0 )+ y′(x0 )(x − x0 )
Уже в случае, когда f (x) - многочлен третьей степени, может случиться,
что последовательность {xn } не сходится к корню при плохом начальном при-
ближении.
Например, в случае, изображенном на рис.2.2,
Рис.2.2 Случай плохого начального приближения в методе Ньютона
Все четные приближения совпадают сa , а нечетные – сb ; метод “зациклился”.
Для более сложных задач реальное поведение приближений xn при пло-
хом начальном приближении становится существенно более запутанным и трудно поддающимся анализу.
12

Если же начальное приближение хорошее, то итерационный метод сходится за 2,3 или 4 итерации.
Из формулы |
xn+1 = xn − |
f (xn ) |
(2) и геометрических построений следует, в |
f ′(xn ) |
частности, что если функция f (x) дифференцируема, и в окрестности корня
f ′(x) не меняет знак, то метод Ньютона сходится, что является достаточным условием сходимости.
Рассмотрим условия сходимости последовательности значений Пусть функция f (x) C 2 ([ab]), тогда
f (x )= 0 = f (xn )+ f ′(xn )(x − xn )+ 12 f ′′(ζ)(x − xn )2
где ζ [x* , xn ] , - формула Тейлора с остаточным членом в форме Лагран-
жа.
Отсюда, разделив на |
f ′(xn ) , получим |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
x |
n |
− |
|
f |
(xn ) |
|
− x |
= |
|
|
1 |
|
|
f ′′(ζ) |
|
|
(x |
n |
|
− x |
* |
)2 , где |
|
x |
n |
− |
f (xn ) |
|
= x |
n+1 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
2 f |
′(xn ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
f ′(xn ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ′(xn ) |
|
|
||||||||||||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x |
|
|
|
− x |
|
|
= |
1 |
|
|
f ′′(ζ) |
|
|
|
|
|
x |
|
− x |
|
2 |
≤ |
|
1 M |
|
|
|
x |
|
− x |
|
2 (3) |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
n+1 |
|
|
|
|
|
|
|
f ′(xn ) |
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
* |
|
|
|
2 |
|
|
|
|
|
|
* |
|
|
|
|
|
|
2 m |
|
|
|
|
* |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
здесь |
M = max |
|
f |
′′ |
|
|
; |
m = |
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
(x) |
min f (x) |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x [ab] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x [ab] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Ясно, что величина ошибки убывает на каждом шаге, если12 Mm xn − x* <1,
тогда xn+1 − x* < xn − x*
Все зависит от начального приближения.
Оценка (3) характеризует скорость убывания погрешности для метода
|
|
|
|
1 |
|
M |
|
|
2 |
′ |
|
|
|
|
|
|
|||||
Ньютона: |
xn+1 |
− x* |
≤ |
|
|
|
|
xn − x* |
|
(3 ) |
2 |
|
m |
|
|||||||
|
|
|
|
|
|
|
|
|
На каждом шаге погрешность пропорциональна квадрату предыдущей погрешности.
Это очень высокая скорость убывания. Например,
x1 – одна точная значащая цифра
13

x2 – две точные значащие цифры x3 – четыре точные значащие цифры x4 – восемь точных значащих цифр
x5 – шестнадцать точных значащих цифр
Замечание
Получить оценки для M и m на практике затруднительно. Чаще всего пользуются критерием:
если xn+1 − xn < ε xn+1 считают заx* .
Кроме того, учитывают ограничение количества итераций: если xn+1 − xn
убывает медленно, но ε невелико, то просто обрывают счет.
Замечание
Если первая и ряд следующих производных обращаются в ноль в точке
′ |
, то формула xn+1 |
|
f (xn ) |
|
сохраняет смысл. |
|
= xn − f ′(xn ) |
||||||
корня, а в окрестности f (x)≠ 0 |
||||||
Таким образом, методом Ньютона можно вычислять и кратные корни. Однако “качество” сходимости теряется.
Пример:
Найти корень уравнения (x −1)= 0 методом Ньютона.
Метод простых итераций.
Рассмотрим наиболее общий итерационный процесс - метод последовательных приближений. Метод Ньютона является его частным случаем.
Уравнение f (x)= 0 (1) |
|
|
|
Представим в видеx = φ(x). |
|
|
|
Так, например, для метода Ньютонаx = x − |
f |
(x) |
. |
f |
′ |
||
|
(x) |
||
Ясно, что существует неограниченное количество способов такого представления, и искомый корень обращает это уравнение в тождество.
x* ≡ φ(x* )
Рассмотрим последовательность значений |
x , которая определяется сле- |
дующим образомxn+1 = φ(xn ), x0 [a, b] задано. |
(4) |
14

Оказывается, что при определенных свойствах функции φ(x) последова-
тельность (4) сходится к корню уравнения (1).
Достаточные условия сходимости формулируются в теореме.
Теорема. Пусть в окрестности искомого корня V* ={x − x* < r} функция φ(x)
удовлетворяет условию Коши – Липшица с константой, меньшей единицы, т.е.
x′, x′′ V* : φ(x′)− φ(x′′) ≤ q x′ − x′′, q = const <1(5)
Тогда последовательность (4) с V* сходится к корню, т.е. xn → x* , и имеет
n→∞
место оценка погрешности:
xn − x* ≤ qn x0 − x* (6).
Доказательство
Разделим доказательство теоремы на две части.
Вначале покажем, что все x , определяемые в (4), принадлежат окрестно-
сти V* корня x* . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Действительно, если |
x V* , y = f (x), то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
y − x* |
|
= |
|
|
|
φ(x)− φ(x* ) |
|
≤ q |
|
x − x* |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Далее, |
|
x |
n |
− x |
|
= |
|
φ(x |
n−1 |
)− φ(x ) |
|
≤ q |
|
x |
n−1 |
− x |
* |
|
, |
откуда |
|
x |
n |
− x |
|
≤ qn |
|
x |
0 |
− x |
* |
|
, т.е. до- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
|||||||||||
казана оценка погрешности (6). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Из условия (6) сразу следует сходимость |
xn → x* . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
||
Замечание
На практике вместо трудно проверяемого условия Коши – Липшица (5) обычно требуют выполнения условия:
φ′(x)V* ≤ q <1 (5’)
из которого в силу теоремы о среднем из математического анализа следует условие Коши – Липшица (5).
Пример:
Методом простых итераций найти корни уравнения x2 − a = 0 (квадратный корень из числаa ).
15

1метод.
x= x2 + x − a , φ(x)= x2 + x − a , φ′(x)= 2x +1 ;
φ′(x) <1 2x +1 <1 x + 12 < 12
Только для x (−1,0) корень будет найден методом простых итераций. 2 метод.
|
a |
|
|
a |
, φ′(x)= − |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
x = |
|
, φ(x)= |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
x |
x |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
′ |
|
|
|
, |
|
a |
|
<1 |
|
|
|
или |
|
x |
|
> |
|
a . |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Условие |
|
φ (x)<1 |
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
т.е. 0 < x |
|
|
< a , и метод “зацикливается”. |
|||||||||||||||
Но при x |
0 |
> |
|
a |
0 < x |
|
= |
|
|
< |
a |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
x0 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Например, x |
0 |
= 2 |
|
a , x |
|
= |
1 |
|
|
a , |
x |
2 |
= 2 |
a , x |
3 |
= |
1 |
a и т.д. |
||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 метод. |
|
|
|||||||
Запишем метод Ньютона |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
x = φ(x), φ(x)= x − |
|
f (x) |
|
|
|
|
|
|
x2 − a |
|
1 |
|
|
a |
|
|
|
|
||||||||||||||||||
|
|
|
= x − |
|
|
|
|
|
|
|
|
= |
|
x + |
|
|
|
. |
|
|
||||||||||||||||
|
′ |
|
2x |
|
|
|
2 |
x |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
f |
(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Теорема (без доказательства). |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Пусть на отрезке x [ab] |
функция |
|
f (x) имеет первую и вторую производ- |
|||||||||||||||||||||||||||||||||
ную постоянного знака, и пусть f (a) f (b)< 0 . |
|
|
|
|||||||||||||||||||||||||||||||||
Тогда, если в точке |
|
x0 f (x0 ) f ′′(x0 )> 0 |
|
|
|
, то начатая с нее последователь- |
||||||||||||||||||||||||||||||
ность {xk } для метода Ньютона монотонно сходится к корню x* (a, b) уравне-
ния f (x)= 0 .
Здесь xk +1 |
|
1 |
|
|
a |
|
2 |
|
|
в точке x = a f (x) ме- |
= |
|
|
+ |
|
|
|
′ |
′′ |
||
|
|
|
||||||||
2 |
xk |
|
, f (x)= x |
|
− a, f (x)= 2x, f |
(x)= 2 |
||||
|
|
|
|
xk |
|
|
|
|
||
|
|
|
|
′′ |
, |
няет знак, и для монотонной сходимости нужно только взять f (x) f (x)> 0 |
|||||
т.е. f (x)> 0, |
|
x |
|
> a . |
|
|
|
|
|||
Так находят квадратный корень с машинной точностью. |
|
||||
16
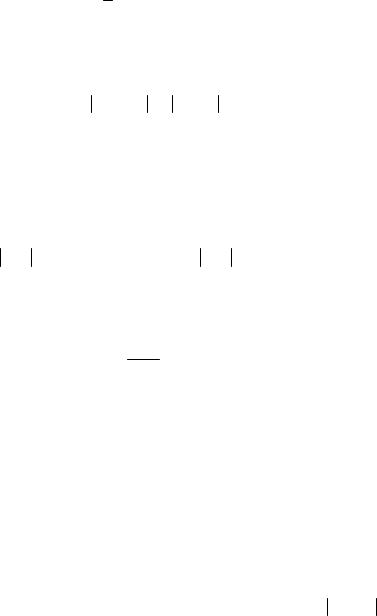
Аналогично находят корень n-той степени изa , т.е. решение уравне-
нияxn − a = 0 .
Замечание
В силу неоднозначности φ(x) практически всегда можно подобратьφ(x),
чтобы в некоторой окрестности корня выполнялось достаточное условие сходимости.
Оценка скорости сходимости метода простых итераций (МПИ).
На каждом шаге погрешность убывает не менее чем в q раз. (Для метода
дихотомииq = 12 ).
Погрешности ведут себя как члены убывающей геометрической прогрессии со знаменателем q .
Иначе: xn+1 − x* ≤ q xn − x* , поэтому говорят, что метод простых итераций МПИ представляет собой линейный итерационный процесс (или метод первого порядка).
Замечание.
Определение имеет смысл, если в малой окрестности корня величина φ′(x)ограничена снизу, т.е. φ′(x) ≥ q0 > 0 .
Пример.
При φ(x)= x − f ((x)) мы получаем метод Ньютона (частный случай МПИ).
f ′ x
Для него можно показать, что |
|
′ |
|
= 0 , поэтому получается квадратичный ите- |
||||||||||||
|
|
|||||||||||||||
φ (x) |
|
|||||||||||||||
рационный процесс (или метод второго порядка). |
||||||||||||||||
Действительно, пусть φ(x)= x − |
|
f (x) |
|
|
|
|
|
|
||||||||
|
f |
′ |
|
|
|
|
|
|
|
|
||||||
|
|
|
(x) f (x)− f (x) |
|
(x) |
|
f (x) f |
|
(x) |
|||||||
|
|
f |
|
f |
(x) |
|
|
|||||||||
′ |
− |
|
′ |
|
|
|
′′ |
= |
|
|
′′ |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
φ (x)=1 |
|
(f (x)) |
2 |
|
|
|
|
|
(f |
(x)) |
2 |
|
||||
|
|
|
′ |
|
|
|
|
|
|
|
′ |
|
|
|||
Так как по предположению f (x* )= 0 , тоφ′(x* )= 0 .
Так как φ′(x* )= 0 иφ(x) C([ab]), то δ > 0 : φ′(x)<1 x O(x* , δ), т.е. достаточное условие сходимости выполняется приx O(x* , δ).
17
Теорема (скорость сходимости итераций Ньютона).
1. Если x* - простой корень, то сходимость является квадратичной,
т.е. |
|
E |
n+1 |
|
≈ |
1 |
|
M |
|
|
E |
n |
|
2 , гдеE |
n |
= x |
n |
− x . |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
2 |
|
m |
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p −1 |
|
|
|
|
|||||
|
|
2. Если |
x* - корень кратности p , то сходимость линейная и |
|
En+1 |
|
≈ |
|
En |
|
. |
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
p |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
18
